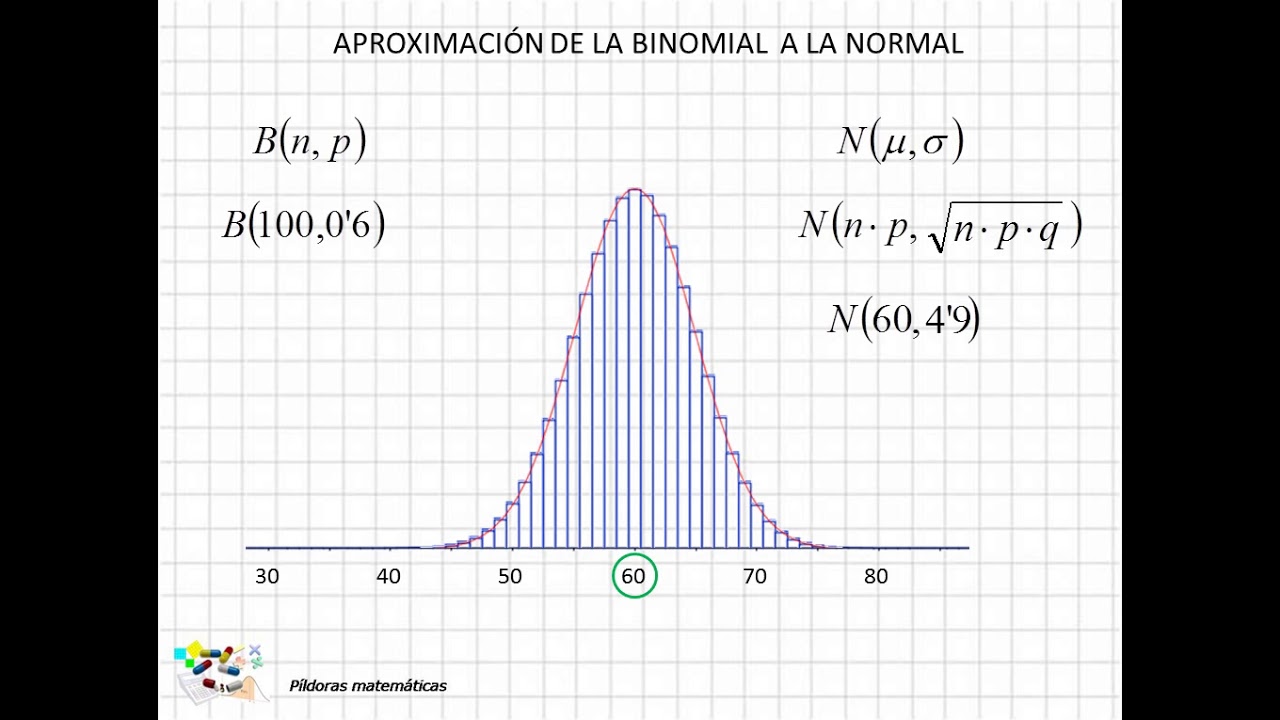
Evolución de la distribución binomial
La distribución binomial es un modelo probabilístico que se utiliza para describir la distribución de probabilidad de tener éxito en un número fijo de ensayos independientes. A medida que el número de ensayos aumenta, la distribución binomial comienza a aproximar la distribución normal. Esta aproximación es fundamental para comprender cómo los eventos probabilísticos se comportan en situaciones del mundo real.
Teorema del límite central
El teorema del límite central es un resultado fundamental en la teoría de la probabilidad y la estadística. Este teorema establece que, a medida que el tamaño de la muestra aumenta, la distribución de la media de las muestras seguirá una distribución normal, sin importar la forma de la distribución original. Este concepto es esencial para comprender la relación entre la distribución binomial y la distribución normal.
Condiciones para la aproximación
La aproximación de la distribución binomial a la distribución normal se basa en ciertas condiciones. Una de las condiciones clave es que el número de ensayos debe ser lo suficientemente grande. Además, la probabilidad de éxito en cada ensayo no debe estar demasiado cerca de 0 o 1. Es importante comprender estas condiciones para aplicar con precisión la aproximación en situaciones reales.
Método de aproximación
El método de aproximación de la distribución binomial a la distribución normal se basa en el uso de la media y la desviación estándar. Al aplicar este método, se calcula la media y la desviación estándar de la distribución binomial y se utilizan para modelar la distribución como una distribución normal. Este enfoque proporciona una manera efectiva de simplificar cálculos y análisis en problemas que involucran la distribución binomial.
Importancia en la práctica
La aproximación de la distribución binomial a la distribución normal tiene una gran relevancia en la práctica. Muchas situaciones del mundo real que involucran eventos probabilísticos pueden modelarse con la distribución binomial, y la capacidad de aproximar esta distribución a una distribución normal facilita significativamente el análisis y la interpretación de los resultados.
Errores comunes y limitaciones
A pesar de su utilidad, la aproximación de la distribución binomial a la distribución normal tiene ciertos errores comunes y limitaciones que se deben tener en cuenta. La principal limitación radica en las condiciones de validez de la aproximación, las cuales deben ser cumplidas para asegurar la precisión de los resultados. Ignorar estas condiciones puede conducir a errores significativos en el análisis.
Aplicaciones en la investigación científica
La aproximación de la distribución binomial a la distribución normal es ampliamente utilizada en la investigación científica. Desde estudios clínicos hasta experimentos en ciencias sociales, esta aproximación proporciona una herramienta poderosa para analizar y comprender los resultados de experimentos que involucran eventos probabilísticos. Su aplicación correcta es crucial para la interpretación precisa de los datos.
Estrategias para verificar la aproximación
Verificar la precisión de la aproximación de la distribución binomial a la distribución normal es fundamental para garantizar la validez de los análisis. Estrategias como el uso de gráficos de probabilidad, pruebas de hipótesis y simulaciones computacionales pueden ayudar a corroborar que la aproximación es adecuada para un conjunto de datos específico. Estas estrategias brindan seguridad en la aplicación de la aproximación en contextos reales.
Consideraciones en la toma de decisiones
Al utilizar la aproximación de la distribución binomial a la distribución normal en la toma de decisiones, es importante considerar las implicaciones de cualquier error en la aproximación. Los riesgos asociados con decisiones basadas en resultados aproximados deben ser cuidadosamente evaluados. Además, es esencial comprender cómo la aproximación afecta la interpretación de los resultados y las conclusiones extraídas de ellos.
Comparación de precisiones
Es crucial comprender las diferencias en precisión entre la distribución binomial y la distribución normal. Aunque la aproximación simplifica el análisis, es fundamental reconocer que la distribución binomial y la distribución normal pueden proporcionar resultados ligeramente diferentes en ciertas situaciones. Esta comparación permite evaluar la validez de la aproximación en contextos específicos y tomar decisiones informadas.
El papel de la tecnología
La tecnología desempeña un papel significativo en la aplicación de la aproximación de la distribución binomial a la distribución normal. El uso de software estadístico y herramientas de simulación permite realizar cálculos y análisis de manera eficiente y precisa. Además, la visualización de los resultados a través de gráficos y representaciones visuales facilita la comprensión de la aproximación y sus implicaciones.
Consideraciones éticas
En la aplicación de la aproximación de la distribución binomial a la distribución normal, es fundamental considerar las implicaciones éticas de los resultados obtenidos. Es importante asegurarse de que cualquier aproximación utilizada sea la más adecuada para el contexto y que los análisis basados en esta aproximación sean éticamente responsables. La transparencia en la comunicación de los métodos utilizados es esencial para garantizar la integridad de los resultados.
La aproximación de la distribución binomial a la distribución normal es una herramienta poderosa en el análisis de eventos probabilísticos. Comprender las condiciones, el método de aproximación, las aplicaciones y las limitaciones de este proceso es fundamental para su aplicación efectiva en situaciones del mundo real. La cuidadosa consideración de la precisión, las implicaciones éticas y el papel de la tecnología garantiza que la aproximación se utilice de manera apropiada y responsable.