Conceptos Fundamentales de Trigonometría
La trigonometría es un área de las matemáticas que se centra en el estudio de las relaciones entre los ángulos y las longitudes de los lados de los triángulos. Las funciones trigonométricas, como el seno, el coseno y la tangente, son fundamentales en este campo y se utilizan para modelar fenómenos periódicos, como el movimiento armónico simple, las ondas y las oscilaciones. En este artículo, nos enfocaremos en el cálculo de los valores de estas funciones para múltiplos específicos de 30, 45 y 60 grados, lo que nos permitirá comprender mejor su comportamiento en situaciones cotidianas y aplicaciones matemáticas más avanzadas.
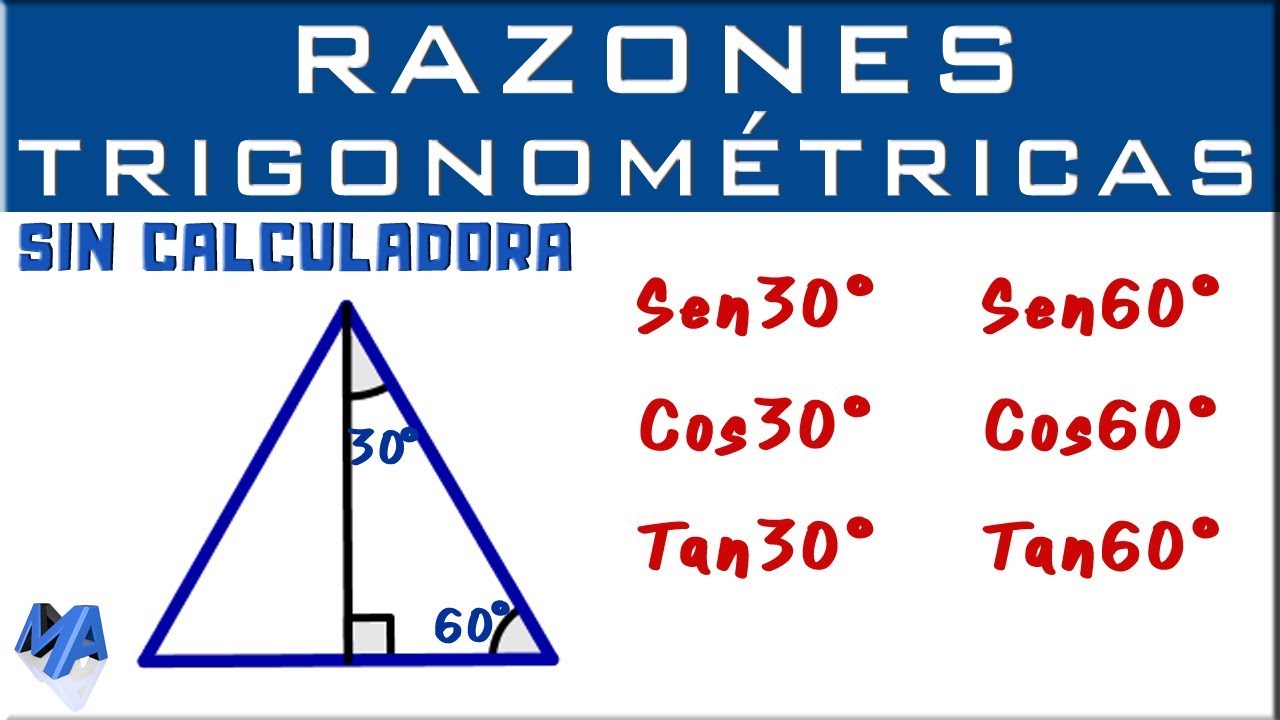
Valor de las Funciones Trigonométricas para 30 Grados
Para calcular el valor de las funciones trigonométricas para 30 grados, primero debemos recordar algunos conceptos básicos. El seno de un ángulo se define como la razón entre el cateto opuesto y la hipotenusa en un triángulo rectángulo, mientras que el coseno es la razón entre el cateto adyacente y la hipotenusa. Por otro lado, la tangente es la razón entre el seno y el coseno del ángulo. Ahora, en el caso específico de 30 grados, podemos utilizar triángulos especiales, como el triángulo equilátero, para determinar los valores exactos de estas funciones.
Cálculo del Seno, Coseno y Tangente para 30 Grados
Empecemos por el seno de 30 grados. En un triángulo equilátero, todos los lados tienen la misma longitud. Si tomamos un ángulo de 30 grados, el lado opuesto será la mitad de la hipotenusa, lo que nos da un valor de 1/2 para el seno. Para el coseno de 30 grados, el cateto adyacente será la mitad de la hipotenusa, lo que también resulta en un valor de 1/2. Finalmente, al calcular la tangente de 30 grados como el cociente entre el seno y el coseno, obtenemos un valor de 1.
Valor de las Funciones Trigonométricas para 45 Grados
Al igual que con 30 grados, el cálculo de las funciones trigonométricas para 45 grados nos lleva a utilizar triángulos especiales para determinar valores exactos. En este caso, nos enfocaremos en el triángulo isósceles, donde dos de sus lados son iguales, formando un ángulo de 45 grados. Esto nos proporciona una base para calcular el seno, coseno y tangente con mayor precisión.
Cálculo del Seno, Coseno y Tangente para 45 Grados
Consideremos el seno de 45 grados en un triángulo isósceles. Dado que en este triángulo los dos lados que forman el ángulo de 45 grados son iguales, el seno será la razón entre la longitud de cualquiera de estos lados y la hipotenusa. En este caso, la longitud de los lados es √2/2, lo que nos da un valor de √2/2 para el seno. Al aplicar el mismo razonamiento para el coseno, encontramos que también es √2/2. Asimismo, la tangente de 45 grados, al ser el cociente entre el seno y el coseno, resulta en un valor de 1.
Valor de las Funciones Trigonométricas para 60 Grados
Para calcular los valores de las funciones trigonométricas para 60 grados, podemos recurrir nuevamente a triángulos especiales, en este caso, el triángulo equilátero. Al comprender la relación de los ángulos y las longitudes de los lados en este tipo de triángulo, podemos determinar con exactitud los valores del seno, coseno y tangente para 60 grados.
Cálculo del Seno, Coseno y Tangente para 60 Grados
En un triángulo equilátero, todos los ángulos internos son de 60 grados. Esto implica que el seno y el coseno de 60 grados serán iguales, ya que el cateto opuesto y el cateto adyacente tendrán la misma longitud, que es la mitad de la hipotenusa, es decir, 1/2. Por lo tanto, tanto el seno como el coseno de 60 grados tienen un valor de 1/2. Al calcular la tangente como el cociente entre el seno y el coseno, obtenemos un valor de 1.
En resumen, el cálculo de los valores de las funciones trigonométricas para múltiplos específicos de 30, 45 y 60 grados nos permite comprender la relación entre los ángulos y las longitudes de los lados en triángulos especiales, lo que a su vez nos brinda una comprensión más profunda de estas funciones y su comportamiento en diversas situaciones. Al dominar estos cálculos para ángulos claves, estamos mejor equipados para aplicar estas herramientas matemáticas en contextos más complejos, como la resolución de problemas de física, ingeniería, ciencias naturales y otras disciplinas donde las funciones trigonométricas desempeñan un papel crucial.
Referencias
1. Stewart, J. (2008). Calculus: Early Transcendentals. Cengage Learning.