¿Qué es la pendiente de una recta?
En matemáticas, la pendiente de una recta es una medida que indica la inclinación o la dirección de dicha recta.
La pendiente se calcula mediante la fórmula m = (y2 – y1) / (x2 – x1), donde (x1, y1) y (x2, y2) son dos puntos diferentes que pertenecen a la recta.
La pendiente puede tener diferentes valores, dependiendo de la relación entre los cambios en el eje x y los cambios en el eje y. Si la pendiente es positiva, la recta se inclina hacia arriba de izquierda a derecha, mientras que si es negativa, se inclina hacia abajo de izquierda a derecha.
Una pendiente de 0 indica que la recta es horizontal, es decir, no tiene inclinación. En cambio, una pendiente infinita indica que la recta es vertical, y no se puede calcular mediante la fórmula anterior.
La pendiente es una medida fundamental en la geometría analítica y es ampliamente utilizada en diversas aplicaciones, como la física, la economía y la ingeniería.
Fórmula para calcular la pendiente de una recta
La pendiente de una recta es un valor numérico que indica cuánto crece o decrece la recta a medida que se mueve en el eje horizontal. Es una medida importante en la geometría y la física, y se utiliza en diversas aplicaciones, como el cálculo de la velocidad, el cambio de posición y la tasa de crecimiento.
La fórmula para calcular la pendiente de una recta se basa en la diferencia entre las coordenadas de dos puntos de la recta. Los puntos se representan mediante las coordenadas (x₁, y₁) y (x₂, y₂).
La fórmula general para calcular la pendiente de una recta es:
m = (y₂ – y₁) / (x₂ – x₁)
Donde m representa la pendiente de la recta.
Para calcular la pendiente, simplemente debes restar las coordenadas y dividir el resultado por la diferencia entre las coordenadas x. Esto te dará el valor de la pendiente.
Por ejemplo, supongamos que tenemos dos puntos en la recta: A(2, 4) y B(6, 8).
Aplicando la fórmula, tenemos:
- x₁ = 2
- y₁ = 4
- x₂ = 6
- y₂ = 8
De esta manera, sustituyendo los valores en la fórmula, obtenemos:
m = (8 – 4) / (6 – 2) = 4 / 4 = 1
Por lo tanto, la pendiente de la recta que pasa por los puntos A(2, 4) y B(6, 8) es igual a 1.
Es importante tener en cuenta que una pendiente positiva indica una recta creciente, mientras que una pendiente negativa indica una recta decreciente. Una pendiente igual a cero indica que la recta es horizontal, y una pendiente infinita indica que la recta es vertical.
En resumen, la fórmula para calcular la pendiente de una recta es m = (y₂ – y₁) / (x₂ – x₁). Esta fórmula nos permite determinar la inclinación de una recta y su dirección en el plano cartesiano.
Ejemplo de cálculo de la pendiente
En matemáticas, la pendiente es una medida de cómo cambia una variable en relación a otra en una función lineal. Calcular la pendiente de una recta es fundamental en muchos campos, como la física, la economía y la geometría.
Método 1: Fórmula de la pendiente
La fórmula general para calcular la pendiente entre dos puntos es:
m = (y2 – y1) / (x2 – x1)
Donde (x1, y1) y (x2, y2) son las coordenadas de los dos puntos en el plano.
Por ejemplo, si tenemos los puntos (2, 5) y (6, 13), podemos calcular la pendiente de la siguiente manera:
m = (13 – 5) / (6 – 2) = 8 / 4 = 2
Por lo tanto, la pendiente de la recta que pasa por estos puntos es 2.
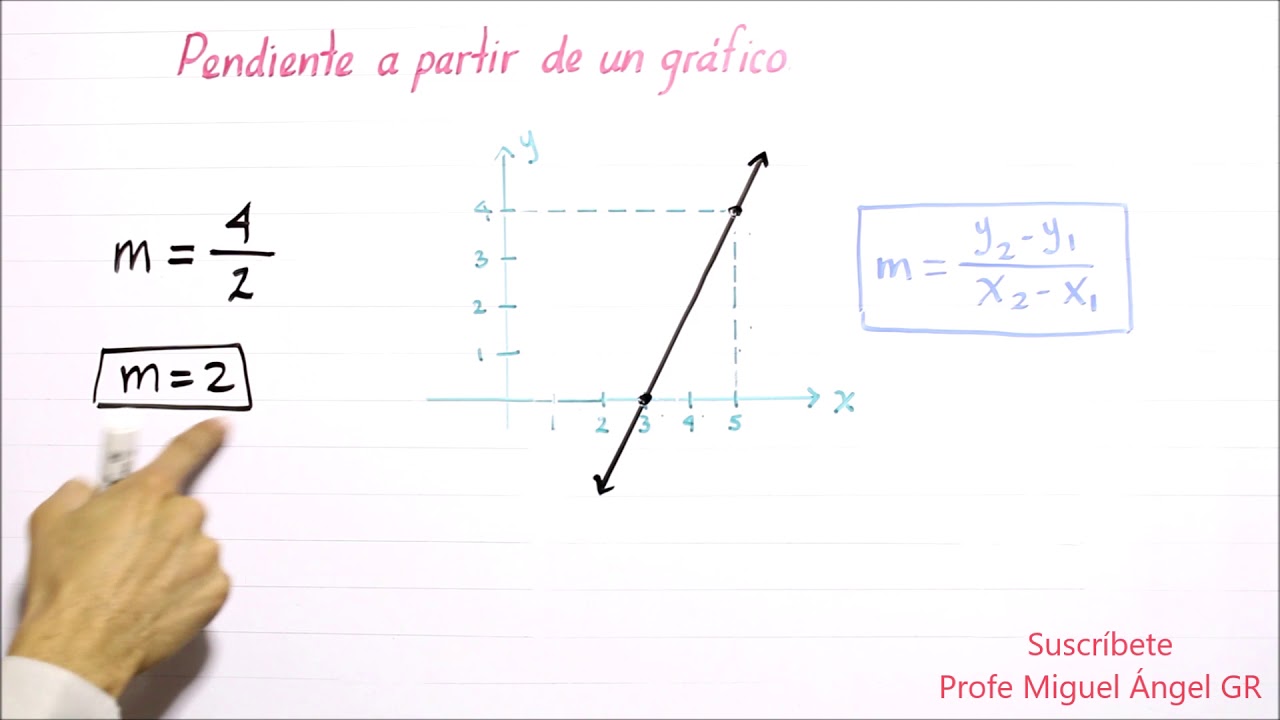
Método 2: Gráfico de la función
Otra forma de calcular la pendiente es a partir del gráfico de la función. Dibuja una recta que pase por los dos puntos dados y elige dos puntos más en la recta. Calcula la diferencia entre las coordenadas «y» de estos dos puntos y divídelo entre la diferencia de las coordenadas «x» correspondientes. El resultado será la pendiente de la recta.
Aplicaciones de la pendiente
El cálculo de la pendiente es útil en muchas situaciones. Por ejemplo, en física, se utiliza para determinar la velocidad de un objeto en movimiento. En economía, puede ser utilizado para analizar el rendimiento financiero o las tendencias de mercado. En geometría, es utilizado para determinar la inclinación de una superficie o una pendiente.
Calcular la pendiente de una recta es esencial para comprender las relaciones entre variables en una función lineal. Utilizando la fórmula de la pendiente o el gráfico de la función, es posible determinar la inclinación de una recta y aplicar este concepto en diversas áreas de estudio.
Interpretación de la pendiente
La pendiente es uno de los conceptos más importantes en el análisis de funciones. Se refiere a la inclinación o la tasa de cambio de una recta o curva en un punto específico.
Para calcular la pendiente de una recta, se utiliza la fórmula m = Δy / Δx, donde Δy representa el cambio en el eje y y Δx representa el cambio en el eje x. Esta fórmula nos indica cuánto crece o decrece la función en relación al desplazamiento horizontal o vertical.
Una pendiente positiva indica que la función está creciendo a medida que nos movemos hacia la derecha en el eje x, mientras que una pendiente negativa indica un decrecimiento. Una pendiente de cero indica que la función es constante, es decir, no crece ni decrece.
Interpretación de la pendiente en contextos reales
En contextos de problemas reales, la pendiente tiene significados relacionados con la situación que se esté analizando. Por ejemplo, si estamos estudiando la temperatura de una ciudad en función del tiempo, la pendiente nos indicará qué tan rápido está aumentando o disminuyendo la temperatura en un periodo de tiempo determinado.
En el caso de una función de costo en función de la cantidad producida de un bien, la pendiente nos dará información sobre el costo adicional asociado a producir una unidad adicional del bien. Si la pendiente es muy pronunciada, significa que el costo adicional es alto, mientras que una pendiente más suave indica un menor costo adicional.
La pendiente y la representación gráfica
Gráficamente, la pendiente se representa por la inclinación de una recta o curva en el plano cartesiano. Una recta con una pendiente positiva sube hacia la derecha, mientras que una pendiente negativa baja hacia la derecha. Una pendiente de cero se representa con una recta horizontal.
Es importante notar que la pendiente de una curva no es constante, sino que puede variar a medida que nos movemos a lo largo de la curva. En estos casos, se utiliza el concepto de la derivada para calcular la pendiente instantánea en un punto determinado.
En resumen, la pendiente es un concepto fundamental en el análisis de funciones y permite interpretar la relación entre las variables en diferentes contextos. Su cálculo nos brinda información valiosa sobre el comportamiento de una función y su representación gráfica.