Un conjunto en probabilidad y estadística es un concepto fundamental que desempeña un papel crucial en la formulación y resolución de problemas en estos campos. Entender la definición y el concepto de conjunto es esencial para aplicar métodos estadísticos y probabilísticos de manera efectiva.
Importancia del conjunto en probabilidad y estadística
Los conjuntos son la piedra angular de la teoría de probabilidad y estadística, ya que proporcionan una forma de organizar y manipular datos y eventos. Al comprender cómo funcionan los conjuntos, los profesionales y estudiantes pueden realizar análisis más precisos y tomar decisiones informadas en diversos contextos, desde la investigación científica hasta la toma de decisiones empresariales. En este artículo, exploraremos en detalle la definición y el concepto de conjunto en el contexto de la probabilidad y la estadística, destacando su importancia en la aplicación práctica.
Definición de conjunto en probabilidad y estadística
Un conjunto en el contexto de la probabilidad y la estadística se refiere a una colección de elementos o eventos distintos y únicos que se agrupan o relacionan de alguna manera. Estos elementos pueden ser datos, variables aleatorias, resultados de experimentos, o cualquier otro tipo de entidad que se esté analizando en un estudio estadístico o probabilístico. La definición precisa de un conjunto en este contexto es fundamental para establecer las bases sobre las cuales se lleva a cabo el análisis y la modelización de fenómenos aleatorios y variables.
Concepto de conjunto en probabilidad y estadística
El concepto de conjunto en la probabilidad y la estadística abarca la noción de inclusión, exclusión, intersección, unión, y complemento de conjuntos, entre otros aspectos. Al comprender estos conceptos, los analistas de datos y los estadísticos pueden describir y comparar diferentes eventos y resultados, lo que les permite tomar decisiones informadas y realizar inferencias significativas sobre poblaciones, muestras, y otros conjuntos de interés.
Operaciones básicas con conjuntos en probabilidad y estadística
Las operaciones básicas con conjuntos, como la unión, la intersección, y el complemento, son fundamentales para el análisis estadístico y probabilístico. La unión de conjuntos combina todos los elementos distintos de dos o más conjuntos, la intersección identifica los elementos comunes a dos o más conjuntos, y el complemento representa todos los elementos que no pertenecen a un conjunto en particular. Estas operaciones son esenciales para la formulación de hipótesis, el cálculo de probabilidades, y la toma de decisiones basada en datos.
Conjuntos disjuntos y conjuntos no disjuntos
En el contexto de la probabilidad y la estadística, los conjuntos disjuntos son aquellos que no comparten elementos en común, es decir, su intersección es un conjunto vacío. Por otro lado, los conjuntos no disjuntos tienen elementos en común y su intersección es un conjunto no vacío. La distinción entre conjuntos disjuntos y no disjuntos es crucial para comprender la relación entre eventos y la probabilidad de que ocurran en conjunto o de manera exclusiva.
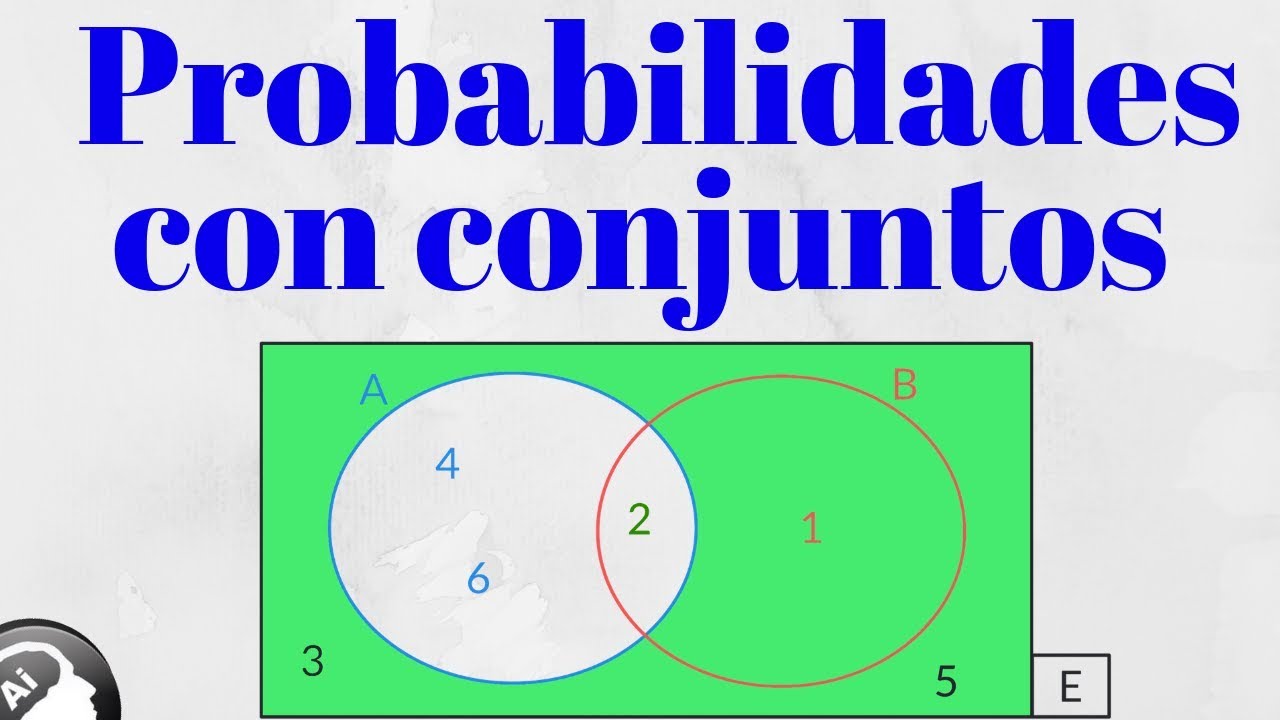
Diagramas de Venn en probabilidad y estadística
Los diagramas de Venn son herramientas visuales poderosas que representan conjuntos y sus relaciones de manera gráfica. En el contexto de la probabilidad y la estadística, los diagramas de Venn se utilizan para ilustrar la intersección, la unión, y la disyunción de conjuntos, lo que facilita la comprensión de la relación de eventos y la visualización de datos en términos de conjuntos y subconjuntos.
Clasificación de conjuntos en probabilidad y estadística
Los conjuntos en el ámbito de la probabilidad y la estadística pueden clasificarse de diversas maneras, como conjuntos finitos, conjuntos infinitos, conjuntos vacíos, conjuntos unitarios, etc. Esta clasificación es importante para organizar y analizar datos en diferentes contextos, desde muestras finitas hasta poblaciones infinitas, y desde eventos seguros hasta eventos imposibles.
Aplicaciones de conjuntos en la modelización estadística
Los conjuntos desempeñan un papel crucial en la modelización estadística de eventos aleatorios y variables. Al utilizar conjuntos para representar datos y eventos, los estadísticos pueden desarrollar modelos matemáticos que describen la variabilidad y las relaciones entre diferentes entidades. Estos modelos son fundamentales para la predicción, la inferencia, y la toma de decisiones basadas en datos en una amplia gama de campos, desde la medicina hasta la ingeniería.
Conjuntos en la teoría de la probabilidad
En la teoría de la probabilidad, los conjuntos desempeñan un papel central en la formulación de espacio muestral, eventos, y variables aleatorias. Al representar eventos como conjuntos, los teóricos de la probabilidad pueden calcular probabilidades, estimar distribuciones, y realizar pruebas de hipótesis con un enfoque riguroso y coherente. Comprender cómo se relacionan los conjuntos con la teoría de la probabilidad es fundamental para interpretar de manera precisa y significativa la incertidumbre y la variabilidad en diversos contextos.
Conjuntos y pruebas estadísticas
En el contexto de las pruebas estadísticas, los conjuntos se utilizan para representar hipótesis nulas, hipótesis alternativas, y regiones críticas. La capacidad de manejar conjuntos de manera efectiva es fundamental para diseñar y ejecutar pruebas de significancia, pruebas de bondad de ajuste, y otras pruebas estadísticas que requieren comparación y evaluación de conjuntos de datos y resultados observados.
Uso de conjuntos en la minería de datos
En el campo de la minería de datos, los conjuntos son fundamentales para la identificación de patrones, la segmentación de datos, y la exploración de relaciones entre variables. Al representar conjuntos de datos de manera adecuada, los profesionales de la minería de datos pueden descubrir información valiosa que impulsa la toma de decisiones empresariales, la personalización de productos y servicios, y la optimización de procesos.
En resumen, los conjuntos desempeñan un papel fundamental en la probabilidad y la estadística al proporcionar una forma clara y coherente de organizar y manipular datos y eventos. Comprender la definición y el concepto de conjunto, así como sus aplicaciones en diversos contextos estadísticos y probabilísticos, es esencial para aplicar métodos analíticos de manera efectiva y tomar decisiones informadas basadas en datos.