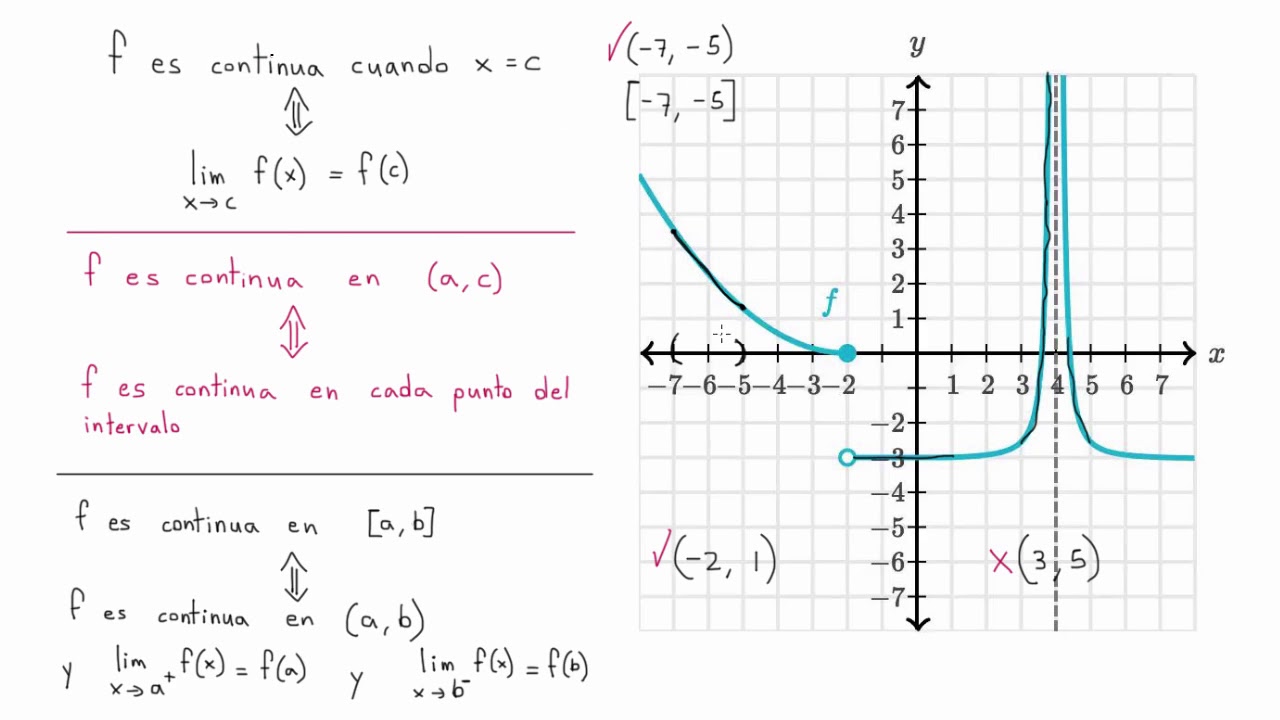
Definición de continuidad
La continuidad es un concepto fundamental en matemáticas que se utiliza para describir la suavidad y fluidez de una función. En la teoría de límites, una función se considera continua en un punto si no hay saltos ni discontinuidades en su gráfico.
Para que una función sea continua, debe cumplir con tres condiciones: la función debe estar definida en el punto en cuestión, el límite de la función debe existir en ese punto y ambos límites (desde la izquierda y desde la derecha) deben ser iguales al valor de la función en ese punto.
La continuidad es importante en muchos aspectos de las matemáticas, especialmente en el cálculo y el análisis matemático. Permite estudiar el comportamiento de una función en un intervalo y facilita la resolución de problemas relacionados con derivadas e integrales.
En resumen, la continuidad de una función nos indica si la función fluye suavemente sin saltos o quiebres en su gráfico. Es un concepto fundamental para comprender y resolver problemas matemáticos relacionados con el cálculo y el análisis.
Criterio de continuidad en un intervalo abierto
El criterio de continuidad en un intervalo abierto se refiere a una condición que debe cumplir una función para ser considerada continua en dicho intervalo.
Para que una función sea continua en un intervalo abierto (a, b), se deben cumplir tres condiciones:
- La función debe estar definida en el intervalo (a, b).
- La función no debe tener saltos ni discontinuidades en ningún punto del intervalo (a, b).
- Para cualquier punto x en el intervalo (a, b), el límite de la función cuando x se acerca a ese punto debe existir y ser igual al valor de la función en ese punto.
Estas condiciones aseguran que la función presenta un comportamiento suave y continuo en el intervalo abierto.
En términos matemáticos, podemos expresar el criterio de continuidad en un intervalo abierto de la siguiente manera:
Una función f(x) es continua en un intervalo abierto (a, b) si y solo si:
- La función está definida en (a, b): f(x) está definida para todo x en (a, b).
- La función no tiene discontinuidades en ningún punto del intervalo (a, b).
- Para todo x0 en (a, b), el límite de f(x) cuando x tiende a x0 existe y es igual al valor de f(x0).
El criterio de continuidad en un intervalo abierto es fundamental en el estudio del análisis matemático, ya que permite determinar si una función es continua en un intervalo dado. Esto, a su vez, tiene implicaciones en otros conceptos y teoremas, como el teorema del valor intermedio y el teorema del valor extremo.
Teorema del Valor Intermedio
El Teorema del Valor Intermedio es un concepto fundamental en el cálculo diferencial que establece una relación entre la continuidad de una función y la existencia de un valor entre dos puntos donde la función toma cualquier valor intermedio.
Este teorema establece que si una función f(x) es continua en el intervalo cerrado [a, b] y M es un valor entre f(a) y f(b), entonces existe al menos un número c en el intervalo (a, b) tal que f(c) = M.
En otras palabras, si tenemos una función continua que va de un punto A a un punto B, de manera que en A la función toma un valor f(a) y en B toma un valor f(b), se puede asegurar que en algún punto intermedio existe un valor igual a cualquier valor que esté entre f(a) y f(b).
Este teorema es de vital importancia en muchas áreas de la matemática y la física, ya que permite garantizar la existencia de soluciones a ecuaciones y problemas de optimización. Además, es utilizado para demostrar otros teoremas y conceptos clave en el cálculo diferencial, como el teorema del valor medio y el teorema fundamental del cálculo.
Una forma común de visualizar este teorema es mediante la interpretación geométrica de la función. Si imaginamos una curva continua que va desde el punto A hasta el punto B, y trazamos una línea horizontal que atraviesa cualquier valor intermedio M, el teorema del valor intermedio nos asegura que en algún punto de la curva, esta línea horizontal se intersectará con la función.
En resumen, el Teorema del Valor Intermedio establece que una función continua en un intervalo cerrado toma todos los valores intermedios entre dos puntos. Este concepto es fundamental en el cálculo diferencial y tiene implicaciones importantes en diversas áreas de las matemáticas y la física.
Teorema de los valores extremos
El teorema de los valores extremos es un principio fundamental en análisis matemático que establece que una función continua en un intervalo cerrado siempre alcanza su valor máximo y mínimo en dicho intervalo.
En otras palabras, si tenemos una función f(x) definida en un intervalo [a, b], donde a y b son los extremos del intervalo, entonces existen puntos c y d en ese intervalo tales que f(c) es el valor máximo de la función y f(d) es el valor mínimo de la función.
Este teorema es muy útil en diversos campos, como la optimización de problemas en economía, física, ingeniería y muchas otras áreas donde se busca encontrar los valores máximos o mínimos de una función.
Un ejemplo sencillo para comprender este teorema sería considerar una función f(x) = x^2 en el intervalo [-2, 2]. Se puede observar que el valor máximo de esta función es f(2) = 4, cuando x = 2, y el valor mínimo es f(-2) = 4, cuando x = -2. Por lo tanto, se cumple el teorema de los valores extremos en este caso.
En resumen, el teorema de los valores extremos establece que una función continua en un intervalo cerrado siempre alcanza su valor máximo y mínimo en ese intervalo. Es un principio fundamental utilizado en diversas áreas de la matemática aplicada.
Ejemplos de funciones continuas en un intervalo abierto
Una función continua es aquella que no presenta saltos, quiebres o discontinuidades en su gráfico. Es decir, su gráfico se puede trazar sin levantar el lápiz. En el caso de un intervalo abierto, estamos hablando de un intervalo en el cual los extremos no están incluidos.
Ejemplo 1: Función lineal
Una función lineal es continua en todo su dominio. Por lo tanto, si consideramos una función lineal en un intervalo abierto, como por ejemplo la función f(x) = 2x + 1 en el intervalo (0, 2), esta función será continua en ese intervalo.
Ejemplo 2: Función exponencial
Una función exponencial del tipo f(x) = a^x, donde «a» es una constante positiva, es continua en todo su dominio. Por lo tanto, si consideramos una función exponencial en un intervalo abierto, como por ejemplo la función f(x) = e^x en el intervalo (−1, 3), esta función será continua en ese intervalo.
Ejemplo 3: Función trigonométrica
Las funciones trigonométricas como el seno, el coseno y la tangente son funciones continuas en todos sus intervalos. Por ejemplo, la función seno f(x) = sin(x) en el intervalo (−π/2, π/2) o la función coseno f(x) = cos(x) en el intervalo (0, π) serían funciones continuas en esos intervalos.
Ejemplo 4: Función logarítmica
Una función logarítmica del tipo f(x) = log(x) es continua en su dominio, siempre y cuando el argumento del logaritmo sea positivo. Por lo tanto, si consideramos una función logarítmica en un intervalo abierto, como por ejemplo la función f(x) = log(x) en el intervalo (1, 5), esta función será continua en ese intervalo.
Estos son solo algunos ejemplos de funciones continuas en un intervalo abierto. Existen muchas otras funciones que cumplen con esta propiedad en diferentes intervalos. Es importante tener en cuenta que la continuidad de una función puede variar dependiendo del intervalo considerado.