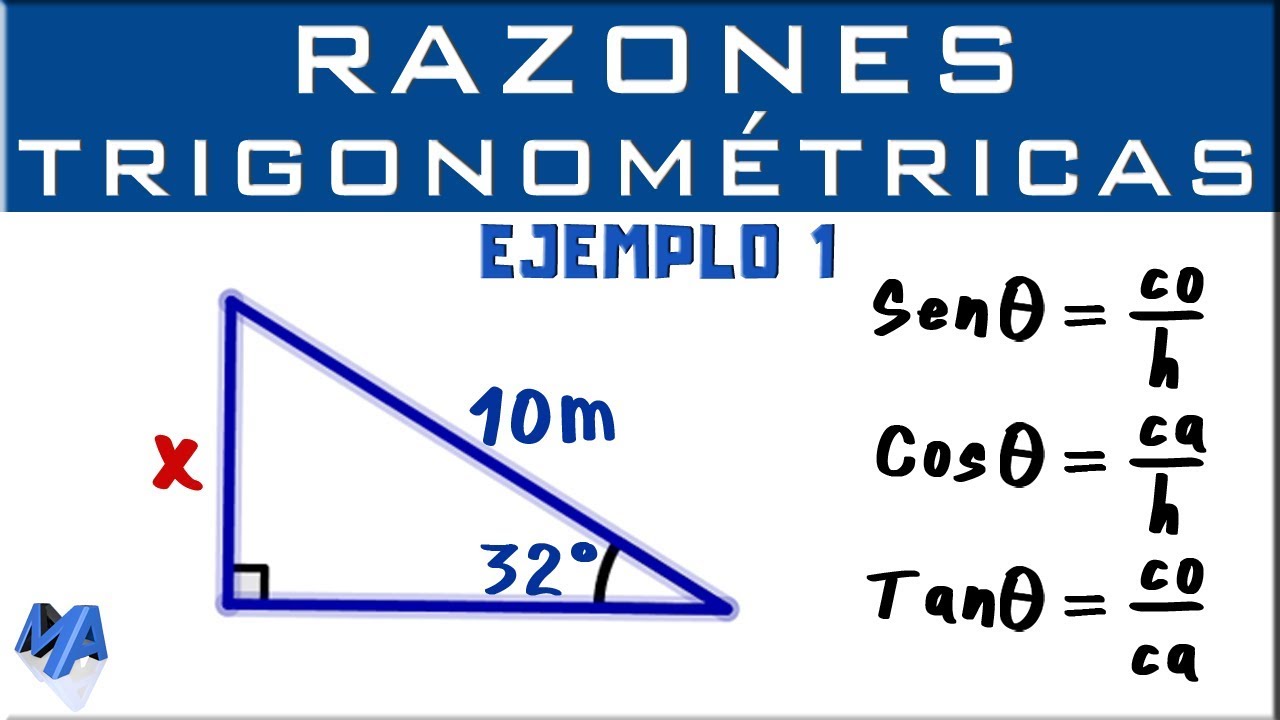
Conceptos básicos de trigonometría
La trigonometría es una rama de las matemáticas que se concentra en las relaciones entre los ángulos y los lados de los triángulos. Una de las funciones trigonométricas fundamentales es el cociente del cateto opuesto dividido por la hipotenusa, también conocido como la definición de la función trigonométrica. Esta función es central para comprender los conceptos trigonométricos y su aplicación en varios campos, desde la física hasta la ingeniería.
Orígenes históricos de la trigonometría
La trigonometría tiene antecedentes que se remontan a las antiguas civilizaciones, como los babilonios y los egipcios, que utilizaban conceptos geométricos para resolver problemas prácticos relacionados con la medición de tierras y la construcción de estructuras. Con el tiempo, la trigonometría se desarrolló y se formalizó, convirtiéndose en una parte esencial de las matemáticas.
La función trigonométrica y su definición
La función trigonométrica es una herramienta clave en el estudio de los triángulos y las relaciones angulares. Su definición, el cociente del cateto opuesto dividido por la hipotenusa, es fundamental para comprender cómo los ángulos y las longitudes de los lados de un triángulo están relacionados. Esta definición es la base de las funciones seno, coseno y tangente, que son fundamentales en la trigonometría.
Relación con el teorema de Pitágoras
La definición de la función trigonométrica está estrechamente relacionada con el famoso teorema de Pitágoras, que establece la relación entre los lados de un triángulo rectángulo. De hecho, el cociente del cateto opuesto dividido por la hipotenusa es una extensión de este teorema y proporciona una forma de analizar la relación entre los ángulos y las longitudes de los lados de un triángulo.
Aplicaciones en la vida cotidiana
Aunque la función trigonométrica puede parecer abstracta, tiene numerosas aplicaciones en la vida cotidiana. Desde la navegación marítima hasta la acústica, la trigonometría es esencial para comprender y resolver una variedad de problemas prácticos. Por ejemplo, los motores de búsqueda utilizan algoritmos trigonométricos para clasificar y presentar información de manera efectiva.
Influencia en la arquitectura y la ingeniería
En el campo de la arquitectura y la ingeniería, la función trigonométrica y su definición son vitales para el diseño de estructuras, la planificación de carreteras y la construcción de edificios. Los profesionales de estos campos utilizan conceptos trigonométricos para calcular ángulos, distancias y cargas, lo que permite la creación de estructuras seguras y eficientes.
Relación con otras funciones trigonométricas
La definición del cociente del cateto opuesto dividido por la hipotenusa establece la base para otras funciones trigonométricas, como el seno, el coseno y la tangente. Estas funciones están interrelacionadas y se utilizan para modelar una variedad de fenómenos naturales y físicos, desde el movimiento de las olas hasta el comportamiento de las ondas sonoras.
Desarrollo de series trigonométricas
La función trigonométrica y su definición han sido fundamentales en el desarrollo de series trigonométricas, que son expansiones matemáticas que representan funciones periódicas en términos de funciones trigonométricas. Estas series tienen aplicaciones en campos como la física teórica, la ingeniería de señales y el procesamiento de imágenes.
Conexiones con el cálculo y la geometría analítica
La función trigonométrica y su definición están intrínsecamente relacionadas con el cálculo y la geometría analítica. En el cálculo, las funciones trigonométricas desempeñan un papel crucial en la modelización de fenómenos periódicos y oscilatorios. En la geometría analítica, las funciones trigonométricas se emplean para describir curvas y graficar puntos en el plano cartesiano.
Aplicaciones en el análisis de movimiento y cambio
En el contexto del cálculo, la función trigonométrica y su definición se utilizan para analizar el movimiento y el cambio. Por ejemplo, la representación de funciones sinusoidales desempeña un papel fundamental en la modelización de fenómenos oscilatorios, como el movimiento armónico simple, que es fundamental en la física y la ingeniería.
Uso en sistemas de coordenadas y transformaciones
Las funciones trigonométricas son esenciales en la representación de puntos y vectores en sistemas de coordenadas polares y en la realización de transformaciones entre sistemas de referencia. Estos conceptos son relevantes en campos como la navegación, la robótica y la física de partículas.
Aplicaciones en la tecnología moderna
En el contexto de la tecnología moderna, la función trigonométrica y su definición son fundamentales en el desarrollo de algoritmos de procesamiento de señales, gráficos por computadora, y la programación de videojuegos. Estos avances tecnológicos dependen en gran medida de las representaciones y manipulaciones de las funciones trigonométricas.
Importancia en la comprensión de ondas y fenómenos periódicos
La función trigonométrica y su definición son esenciales para comprender los conceptos de ondas y fenómenos periódicos en campos como la física, la acústica, la óptica y la electrónica. Las funciones sinusoidales modeladas por la función trigonométrica son la base para comprender la propagación de ondas y la naturaleza cíclica de varios procesos naturales.
Aplicaciones en la música y el sonido
La función trigonométrica y sus aplicaciones se pueden observar claramente en el campo de la música y el sonido. Las ondas sonoras, que se pueden modelar con funciones trigonométricas, son fundamentales para comprender la producción y la percepción del sonido. Los principios trigonométricos también son cruciales en la producción y el diseño de equipos de audio.
Desarrollos contemporáneos en la teoría de números
La función trigonométrica y sus propiedades también desempeñan un papel importante en la teoría de números y en el estudio de las funciones especiales. Los desarrollos contemporáneos en este campo han revelado conexiones profundas entre funciones trigonométricas, la teoría de grupos y la teoría de los números primos.
Aplicaciones en la criptografía y la seguridad informática
La teoría de números y las funciones trigonométricas juegan un papel crucial en el diseño de algoritmos de criptografía y en la seguridad informática. Las propiedades matemáticas de las funciones trigonométricas son fundamentales para el desarrollo de sistemas de encriptación y la protección de datos en la era digital.
En resumen, la función trigonométrica y su definición como el cociente del cateto opuesto dividido por la hipotenusa son fundamentales en las matemáticas y tienen una amplia gama de aplicaciones en diversos campos, desde la física y la ingeniería hasta la música y la seguridad informática. Comprender la función trigonométrica es esencial para abordar problemas complejos y para desarrollar soluciones innovadoras en el mundo moderno.