Entendiendo la diferencia fundamental
Al estudiar física, es crucial comprender la distinción entre magnitud escalar y vectorial. A menudo, los estudiantes luchan por diferenciar entre estas dos cantidades, lo que puede llevar a confusiones durante la resolución de problemas y la interpretación de conceptos. En este artículo, exploraremos en detalle las características distintivas de las magnitudes escalares y vectoriales, proporcionando ejemplos concretos y una explicación detallada para una comprensión más clara.
Diferencias conceptuales
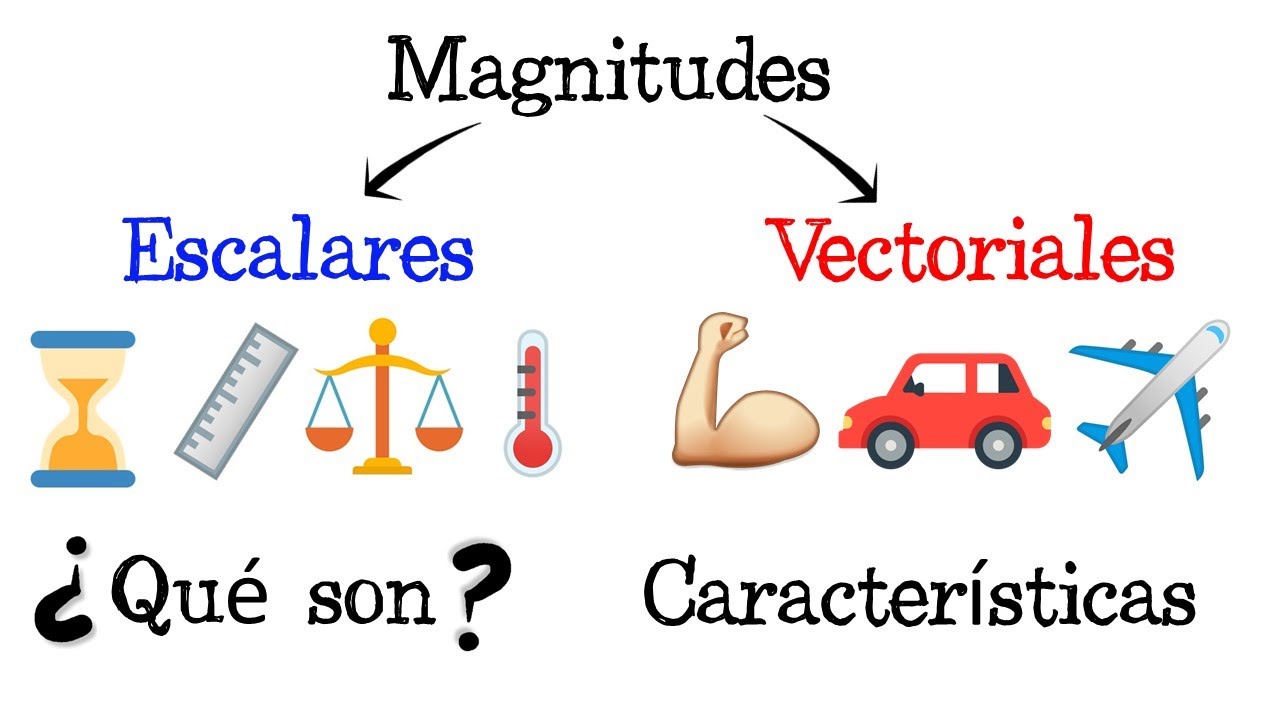
Las magnitudes escalares y vectoriales representan conceptos fundamentales en la física, cada uno con propiedades características que los distinguen claramente entre sí. Una magnitud escalar se caracteriza únicamente por su valor numérico, sin incluir dirección ni sentido. Por otro lado, una magnitud vectorial no solo posee un valor numérico, sino que también tiene dirección y sentido. Esta distinción conceptual es esencial para comprender cómo estas cantidades se aplican en el mundo real y en la resolución de problemas físicos.
Ejemplos de magnitudes escalares
Las magnitudes escalares incluyen conceptos como la temperatura, la masa, la energía, la velocidad y el tiempo. Estas cantidades solo requieren un número y una unidad de medida para ser completamente especificadas. Por ejemplo, la temperatura de un objeto puede ser 25 grados Celsius, la masa de un objeto puede ser 10 kilogramos, o la energía de un sistema puede ser 100 julios. En todos estos casos, la magnitud es completamente descrita por un número y una unidad, sin la necesidad de indicar dirección o sentido.
Aplicaciones cotidianas
Las magnitudes escalares son comunes en la vida diaria, ya que representan cantidades que no requieren dirección para ser completamente significativas. Por ejemplo, al informar la temperatura exterior, estamos proporcionando una magnitud escalar que indica simplemente la cantidad de calor presente en el ambiente. Del mismo modo, al describir la masa de un objeto, estamos comunicando una cantidad que no está relacionada con la dirección o el sentido del objeto en cuestión.
Ejemplos de magnitudes vectoriales
En contraste, las magnitudes vectoriales incluyen conceptos como la velocidad, la aceleración, la fuerza y el desplazamiento. Estas cantidades requieren tanto un valor numérico como una dirección específica para ser completamente definidas. Por ejemplo, una velocidad de 50 kilómetros por hora hacia el norte o una fuerza de 100 newtons hacia abajo representan magnitudes vectoriales, ya que incluyen tanto la cantidad como la dirección en la que actúan.
Importancia en la física
Las magnitudes vectoriales son fundamentales en la descripción del movimiento y las interacciones físicas. La dirección y el sentido de una magnitud vectorial son críticos para comprender cómo actúan las fuerzas, cómo se mueven los objetos y cómo interactúan entre sí. Sin la consideración de la dirección y el sentido, no sería posible comprender completamente el comportamiento de sistemas físicos complejos.
Operaciones matemáticas
Cuando se trabaja con magnitudes vectoriales, es necesario realizar operaciones específicas que tengan en cuenta tanto la cantidad como la dirección. La suma de vectores, la resta de vectores y la descomposición de vectores son operaciones matemáticas que permiten manipular cantidades vectoriales de manera efectiva. Estas operaciones son fundamentales para resolver problemas de física que involucran movimientos, fuerzas y desplazamientos en diversas direcciones.
Combinación de magnitudes
En muchas situaciones físicas, es necesario combinar tanto magnitudes escalares como vectoriales para obtener una comprensión completa de un fenómeno o un sistema. Por ejemplo, al describir el movimiento de un objeto, es esencial considerar tanto la velocidad (magnitud vectorial) como el tiempo transcurrido (magnitud escalar) para calcular la distancia recorrida. Esta combinación de cantidades proporciona un enfoque holístico para abordar problemas físicos complejos.
Visualización en el espacio
Las magnitudes vectoriales son especialmente útiles para representar cantidades que tienen una orientación espacial específica. Por ejemplo, al representar la fuerza ejercida sobre un objeto en un sistema tridimensional, la dirección y el sentido de la fuerza se vuelven crucial para comprender su efecto total sobre el objeto. Esta capacidad de representar información espacialmente es esencial en la modelización y resolución de problemas físicos y de ingeniería.
Importancia en la ingeniería
En disciplinas como la ingeniería civil, mecánica y aeroespacial, el uso de magnitudes vectoriales es fundamental para el diseño y la comprensión de sistemas complejos. La capacidad de definir fuerzas, movimientos y desplazamientos con precisión direccional es crucial para garantizar la seguridad y eficacia de las soluciones ingenieriles en diferentes contextos.
Relación con la geometría
Las magnitudes vectoriales tienen una estrecha relación con las nociones geométricas, ya que representan cantidades que tienen una dirección y sentido específico en el espacio. La representación gráfica de cantidades vectoriales a menudo utiliza sistemas de coordenadas y vectores posicionales para visualizar claramente la dirección y magnitud de una cantidad determinada. Esta conexión con la geometría amplía el alcance de las magnitudes vectoriales más allá de la física, abarcando conceptos matemáticos y geométricos esenciales.
En campos como la navegación marítima y aérea, las magnitudes vectoriales son esenciales para calcular rutas, velocidades y empujes necesarios para el movimiento preciso de vehículos. La consideración de la dirección y el sentido en la planificación de trayectorias y la corrección de desviaciones es crucial para garantizar la seguridad y eficiencia en la navegación en entornos complejos.
En resumen, la distinción entre magnitudes escalares y vectoriales es fundamental para comprender una amplia gama de fenómenos físicos y matemáticos. Las magnitudes escalares representan cantidades puramente numéricas, mientras que las magnitudes vectoriales incluyen dirección y sentido. Esta distinción es crucial en campos que van desde la física y la ingeniería hasta la navegación y la geometría. Al comprender las características y aplicaciones de estas magnitudes, los estudiantes y profesionales pueden desarrollar una comprensión más profunda de cómo se representan y utilizan las cantidades en diversos contextos.