Conceptos fundamentales de geometría
La geometría es una rama de las matemáticas que se concentra en el estudio de las formas, tamaños, y posiciones de los objetos. En la geometría elemental, es esencial comprender conceptos básicos como la recta, la semirrecta y el segmento. Estos conceptos son fundamentales para comprender las propiedades y relaciones espaciales entre puntos, líneas y figuras en el plano.
La recta, la semirrecta y el segmento son términos comunes en geometría, pero a menudo generan confusión. ¿Cuáles son las diferencias clave entre ellos? Vamos a explorar en detalle cada uno de estos conceptos para comprender mejor su distinción.
La recta: una dimensión infinita
Una recta es, quizás, uno de los conceptos más primitivos e elementales en geometría. Se define como una sucesión infinita de puntos que se extiende en ambas direcciones sin fin. Visualmente, se puede imaginar como una línea recta que se prolonga indefinidamente en ambas direcciones. Una recta no tiene principio ni fin, lo que significa que no tiene puntos extremos.
Características de una recta
Una recta se representa con una letra minúscula, como «r,» «s,» o «t,» y se denota con dos puntos en sus extremos, por ejemplo, «r →», para indicar que la recta «r» se extiende infinitamente en ambas direcciones. Una recta, por lo tanto, está compuesta por infinitos puntos que yacen sobre ella sin ninguna separación, lo que la diferencia claramente del concepto de un segmento o semirrecta.
La semirrecta: una extensión finita desde un punto
Una semirrecta es un tipo de línea que comparte algunas similitudes con la recta, pero posee una diferencia crucial. A diferencia de una recta, una semirrecta tiene un principio (o punto de origen) pero se extiende infinitamente en una sola dirección. Visualmente, se puede pensar en ella como una línea que comienza en un punto y se prolonga indefinidamente en una sola dirección.
Representación de una semirrecta
Una semirrecta se denota utilizando un solo punto y una flecha para indicar la dirección en la que se extiende. Por ejemplo, «→ AB» denota la semirrecta que comienza en el punto A y se extiende indefinidamente en la dirección de B. Esta distinción de tener un punto de origen y extenderse en una sola dirección la diferencia notablemente de una recta o un segmento.
El segmento: una porción finita de una línea
El segmento es también una forma de línea, pero en lugar de extenderse infinitamente, tiene un principio y un fin claramente definidos. En otras palabras, un segmento es una porción finita de una recta que une dos puntos especificados.
Características distintivas de un segmento
Un segmento se denota utilizando una línea sobre las letras que representan los puntos del segmento. Por ejemplo, «AB» representa el segmento que conecta los puntos A y B. Es importante notar la longitud finita del segmento y que tiene puntos extremos claramente definidos, lo que lo diferencia tanto de una recta como de una semirrecta.
Comparación visual entre recta, semirrecta y segmento
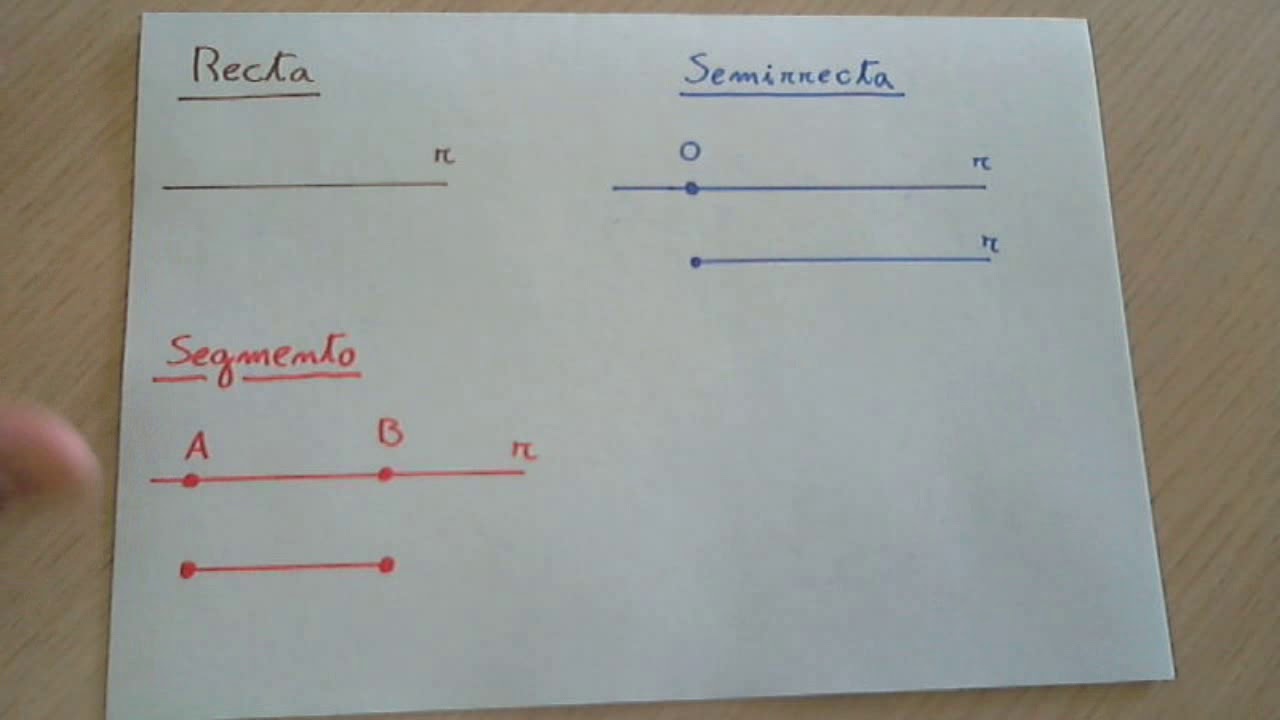
Para comprender mejor la distinción entre estos conceptos, es útil visualizar cada uno de ellos en un plano cartesiano. Imagina una línea horizontal que compartimenta el espacio de extensión infinita en ambas direcciones; eso representa una recta. En contraste, una semirrecta es como una línea que irradia en una sola dirección desde un punto de origen. Por último, un segmento se asemeja a una línea finita que conecta dos puntos específicos en el plano.
Fácil posesión visual de las diferencias
Al comprender estas definiciones y visualizar representaciones gráficas de cada concepto, se vuelve más sencillo apreciar sus distintas propiedades y comprender cómo se relacionan entre sí en el plano geométrico.
Usos y aplicaciones en la vida cotidiana
A pesar de ser conceptos abstractos en el ámbito matemático, las rectas, semirrectas y segmentos tienen aplicaciones prácticas en la vida cotidiana. Por ejemplo, al trazar una línea recta para cortar un trozo de papel, estamos utilizando el concepto de una recta. Del mismo modo, al dibujar una línea desde un punto de origen en una dirección específica, estamos haciendo uso de una semirrecta. La utilización de segmentos es evidente cuando marcamos la distancia entre dos puntos en un mapa o medimos un trozo de madera para cortarlo a una longitud precisa.
Relevancia en diversas disciplinas
Más allá de la geometría pura, estos conceptos son fundamentales en campos como la arquitectura, la ingeniería y la cartografía. La comprensión de las propiedades y distinciones entre rectas, semirrectas y segmentos es crucial para el diseño preciso de estructuras, la elaboración de planos y mapas, así como en múltiples aplicaciones prácticas en el desarrollo de productos y dispositivos tecnológicos.
Resolución de problemas matemáticos
En la resolución de problemas matemáticos, comprender la diferencia entre rectas, semirrectas y segmentos es esencial para manipular y operar con líneas y figuras en el plano. La habilidad para identificar y distinguir entre estos conceptos es fundamental al resolver ecuaciones lineales, calcular distancias y trabajar con vectores y direcciones en el espacio tridimensional.
Importancia en la educación matemática
En el contexto educativo, la enseñanza y comprensión de estos conceptos desde una etapa temprana sienta las bases para la comprensión más avanzada de la geometría y el álgebra. Las diferencias entre rectas, semirrectas y segmentos proporcionan una estructura conceptual crucial para el desarrollo del pensamiento lógico y la resolución de problemas matemáticos más complejos en niveles posteriores de educación.
Aplicaciones en el campo de la física
Además de las matemáticas, los conceptos de rectas, semirrectas y segmentos tienen aplicaciones relevantes en la física. En el estudio de la cinemática, por ejemplo, se utilizan rectas para representar trayectorias de partículas en el espacio. Las leyes del movimiento de objetos en línea recta son fundamentales en la mecánica clásica y tienen implicaciones en el diseño y análisis de sistemas mecánicos y estructurales.
Modelado de trayectorias y movimientos
Al modelar el movimiento de partículas, cuerpo rígidos, o sistemas mecánicos, la representación precisa de trayectorias y segmentos de movimiento es esencial. La conceptualización clara de la diferencia entre rectas, semirrectas y segmentos permite una modelización precisa en el análisis de sistemas físicos en el espacio y el tiempo.
En resumen, la distinción entre rectas, semirrectas y segmentos es esencial para comprender las propiedades fundamentales de las líneas y las figuras en el plano. Estos conceptos no solo son fundamentales en la geometría matemática, sino que tienen aplicaciones prácticas en diversos campos, desde la arquitectura y la ingeniería hasta la física y la cartografía. La capacidad para distinguir y utilizar estos conceptos con precisión es crucial para el desarrollo del pensamiento lógico, la resolución de problemas matemáticos y la modelización precisa en el estudio de fenómenos físicos.