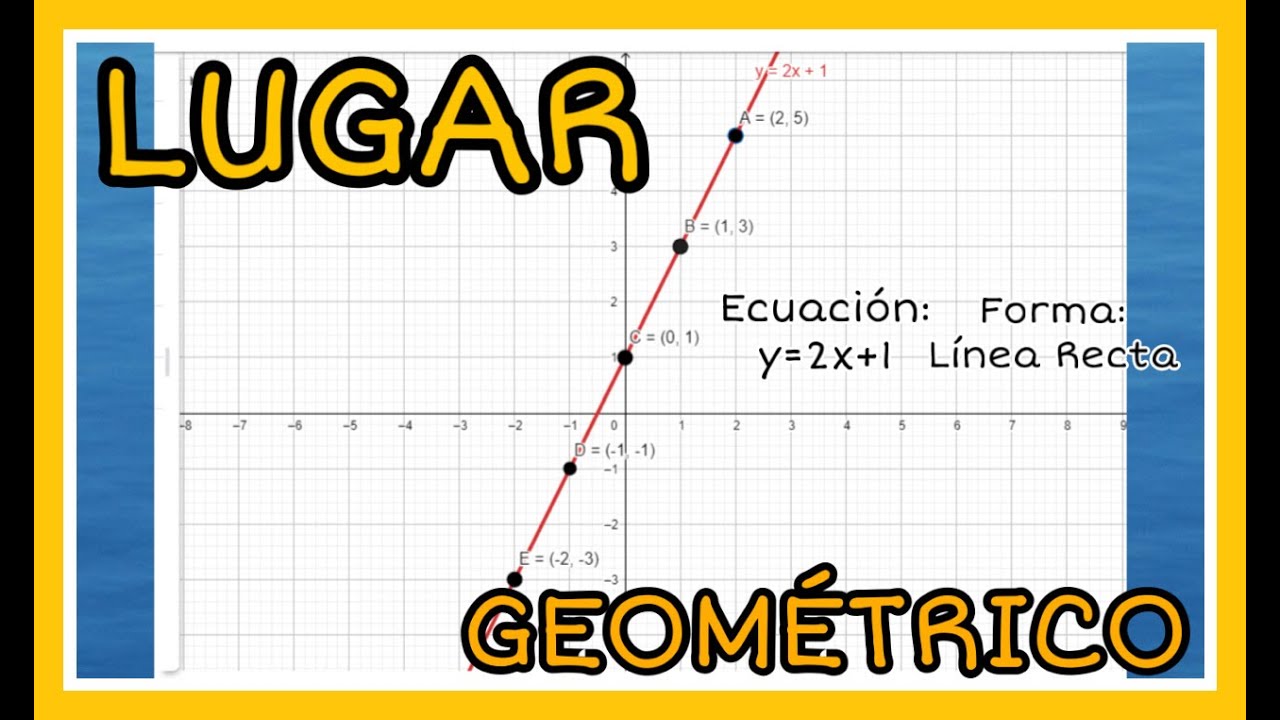
Comenzando la exploración
La geometría analítica es una rama de las matemáticas que combina la geometría con conceptos del álgebra. Una de las principales ideas de la geometría analítica es el estudio de la recta como un «lugar geométrico», es decir, el conjunto de puntos que satisfacen ciertas condiciones. En este artículo, nos sumergiremos en el fascinante concepto de la recta en geometría analítica, explorando sus propiedades, ecuaciones y aplicaciones, con el fin de comprender en profundidad su significado y relevancia en el campo matemático.
Las bases de la recta en geometría
Para comprender la recta en geometría analítica, es fundamental tener claros algunos conceptos básicos. La recta puede ser definida como el conjunto de puntos que satisface una ecuación lineal de la forma (Ax + By = C), donde (A), (B) y (C) son constantes reales, con (A) y (B) no ambos iguales a cero. Esta ecuación representa una representación general de la recta en el plano cartesiano, donde (x) e (y) son las coordenadas de un punto en el sistema de ejes coordenados.
La ecuación general de la recta
La ecuación general de la recta, (Ax + By = C), presenta un aspecto fundamental en la comprensión de la recta en geometría analítica. Esta ecuación nos proporciona información crucial sobre la pendiente y la intersección con los ejes coordenados. La pendiente, denotada como (m), se calcula como (-frac{A}{B}), y la intersección en el eje (y), denotada como (b), es (frac{C}{B}) cuando (B neq 0). Además, esta ecuación nos permite determinar si la recta es paralela a alguno de los ejes coordenados.
La ecuación punto-pendiente
Otra forma común de representar una recta es mediante la ecuación punto-pendiente, (y – y_1 = m(x – x_1)), donde (m) es la pendiente de la recta y ((x_1, y_1)) es un punto en la recta. Esta forma de la ecuación nos ofrece una comprensión más intuitiva de cómo la pendiente y un punto determinado definen de manera única una recta en el plano cartesiano.
La ecuación pendiente-intercepto
Además de la ecuación general y la ecuación punto-pendiente, existe la forma conocida como la ecuación pendiente-intercepto, (y = mx + b), donde (m) representa la pendiente y (b) es la intersección en el eje (y). Esta forma es especialmente útil para visualizar gráficamente la recta y comprender su pendiente y su intersección con el eje (y).
Propiedades y características
Las rectas en geometría analítica poseen diversas propiedades y características que las hacen objetos matemáticos fascinantes de estudiar. Estas propiedades incluyen la pendiente, la perpendicularidad, la paralelismo, la intersección de rectas, entre otras. Explorar estas propiedades nos permite comprender mejor cómo las rectas se comportan en el plano cartesiano y cómo interactúan entre sí.
La pendiente de una recta
La pendiente de una recta es un concepto fundamental que define su inclinación. Una pendiente positiva indica una inclinación hacia arriba, mientras que una pendiente negativa indica una inclinación hacia abajo. Una pendiente nula representa una recta horizontal, y una pendiente infinita corresponde a una recta vertical. Comprender la pendiente es crucial para interpretar el comportamiento y la dirección de una recta en el plano.
Intersección de rectas
Cuando se trabaja con varias rectas en el plano cartesiano, es importante comprender cómo estas interactúan entre sí. La intersección de dos rectas puede ocurrir en un punto, lo que indica que las rectas se cruzan, o pueden ser paralelas o coincidentes. Estudiar estos casos nos permite entender las relaciones espaciales entre distintas rectas y cómo se relacionan en el contexto del sistema de coordenadas.
Aplicaciones en geometría y física
El concepto de la recta en geometría analítica tiene numerosas aplicaciones en diversas áreas, desde problemas de localización en geometría hasta la modelización de fenómenos físicos en el mundo real. En geometría, las rectas proporcionan la base para la construcción y la visualización de figuras, mientras que en física, las ecuaciones de las rectas pueden representar trayectorias y movimientos de objetos.
La recta como modelo de fenómenos físicos
En el ámbito de la física, las ecuaciones de las rectas se utilizan para modelar diversos fenómenos, como el movimiento rectilíneo uniforme o la propagación de ondas. La capacidad de representar gráficamente estas ecuaciones nos brinda una comprensión intuitiva de los conceptos físicos subyacentes y nos permite realizar predicciones sobre el comportamiento de los sistemas en estudio.
Resolución de problemas de intersección y posición
En geometría, el uso de ecuaciones de rectas nos permite resolver problemas relacionados con la posición relativa de puntos, rectas y figuras en el plano. La capacidad de determinar la intersección de rectas o la posición de un punto respecto a una recta es crucial para la resolución de diversos problemas geométricos, como la ubicación de puntos de intersección o la determinación de ángulos.
La recta en sistemas de coordenadas tridimensionales
Si bien hemos explorado el concepto de la recta en el plano bidimensional, es importante destacar que la geometría analítica se extiende al espacio tridimensional. En sistemas de coordenadas tridimensionales, las rectas se definen mediante ecuaciones de la forma (Ax + By + Cz = D), lo que nos permite estudiar líneas rectas en el espacio y comprender su intersección y orientación en un contexto tridimensional.
Usos avanzados en álgebra lineal y cálculo
El estudio de las rectas en geometría analítica sienta las bases para conceptos más avanzados en matemáticas, como el álgebra lineal y el cálculo. En álgebra lineal, las rectas se generalizan como subespacios vectoriales, mientras que en cálculo, las ecuaciones de las rectas se utilizan para comprender conceptos de derivadas e integrales en un contexto geométrico.
En resumen, la exploración del concepto de la recta en geometría analítica nos ha permitido comprender su significado como un «lugar geométrico» que puede ser representado de múltiples formas y que tiene aplicaciones en diversos campos de las matemáticas y la física. Las propiedades, ecuaciones y aplicaciones de las rectas nos brindan herramientas poderosas para comprender y modelar fenómenos geométricos y físicos en el mundo real. La recta no solo es un concepto central en el estudio de la geometría analítica, sino que también es un pilar fundamental para el desarrollo de conceptos matemáticos más avanzados.