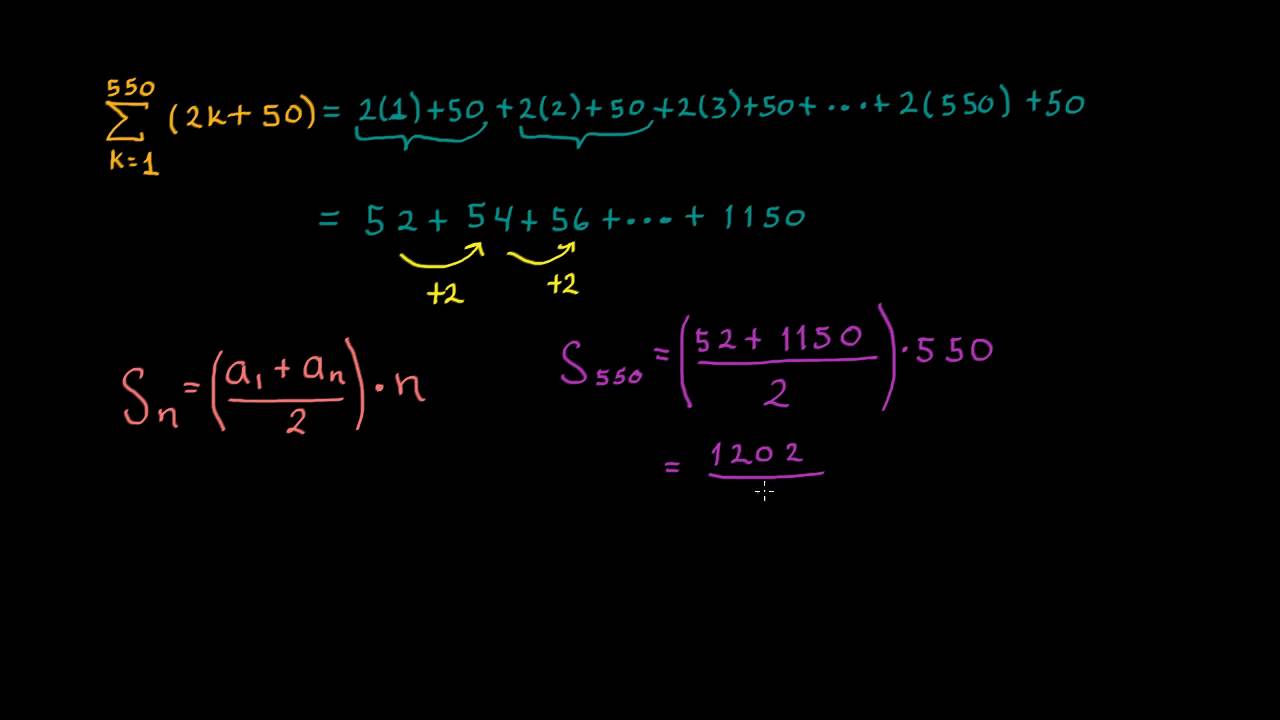¿Qué son las series finitas y las series infinitas?
Las series finitas son sumas de un número limitado de términos, es decir, tienen un inicio y un final definidos. Por ejemplo, la serie finita 1 + 2 + 3 + 4 + 5.
Por otro lado, las series infinitas son sumas de un número infinito de términos, es decir, no tienen un final definido. Estas series pueden converger hacia un valor finito o diverger, es decir, no tener un valor final determinado. Un ejemplo de serie infinita es la serie armónica 1 + 1/2 + 1/3 + 1/4 + 1/5 + …
En las series finitas, la suma de todos los términos resulta en un valor finito. En cambio, en las series infinitas, la suma puede ser finita o infinita, dependiendo de si converge o diverge.
Propiedades y comportamiento de las series finitas
En matemáticas, una serie finita es una secuencia de números o términos que tienen un inicio y un final con una cantidad determinada de elementos. Estas series tienen algunas propiedades y comportamientos interesantes que vale la pena analizar.
Propiedades de las series finitas:
- Inicio y fin determinados: A diferencia de las series infinitas, las series finitas tienen un punto de inicio y un punto de final claramente definidos. Esto significa que se puede contar el número exacto de términos en la serie.
- Suma finita: Al ser una serie con un número limitado de términos, la suma de todos los elementos de la serie también es finita. Esto facilita el cálculo y la comprensión de la serie.
- Orden de los términos: En una serie finita, el orden de los términos es relevante. Cambiar el orden puede resultar en una serie con una suma totalmente diferente.
Comportamiento de las series finitas:
Las series finitas se comportan de manera diferente a las series infinitas debido a su naturaleza limitada. Algunos de los comportamientos más comunes son los siguientes:
- Convergencia: Una serie finita siempre converge, es decir, su suma tiene un valor finito. Esto contrasta con las series infinitas que pueden converger o diverger.
- Tendencia a la estabilidad: Dado que las series finitas tienen un número finito de términos, tienden a ser más estables y predecibles en términos de su suma y comportamiento general.
- Posibilidad de operaciones algebraicas: Las series finitas permiten la realización de operaciones algebraicas y aritméticas más fácilmente en comparación con las series infinitas. Esto se debe a que todos los términos y la suma son finitos.
En conclusión, las series finitas son secuencias de términos con un inicio y un fin determinados. Tienen propiedades como la suma finita y el orden relevante, y se comportan de manera distinta a las series infinitas, siendo más estables y permitiendo operaciones algebraicas más sencillas.
Propiedades y comportamiento de las series infinitas
En matemáticas, una serie infinita es la sucesión de sumas de los términos de una sucesión. La teoría de las series infinitas es una parte importante del análisis matemático y tiene diversas aplicaciones en varias ramas de la ciencia y la ingeniería.
Existen diferentes tipos de series infinitas, pero todas comparten algunas propiedades destacadas. Una de estas propiedades es la convergencia o divergencia de la serie. Una serie convergente es aquella cuya suma tiende a un límite finito a medida que se suman más y más términos. Por otro lado, una serie divergente es aquella cuya suma no tiene un límite finito, es decir, se aleja hacia infinito o se oscila entre diferentes valores.
La convergencia o divergencia de una serie se puede determinar mediante diferentes criterios. Uno de los criterios más conocidos es el criterio de convergencia de Cauchy, que establece que una serie converge si y solo si para cualquier número positivo ε, existe un número natural N tal que, para todo n y m mayores que N, la suma de los términos desde n hasta m es menor que ε.
Otro criterio comúnmente utilizado es el criterio de la razón, que establece que si el límite del valor absoluto de la razón entre dos términos consecutivos de la serie es menor que 1, entonces la serie converge.
Las series infinitas también tienen comportamientos interesantes, como la posibilidad de manipular los términos de la serie para obtener nuevas series. Por ejemplo, la suma de dos series convergentes también es una serie convergente. Además, se pueden aplicar operaciones como la multiplicación o la división de una serie por una constante para obtener una nueva serie.
En resumen, las series infinitas son una herramienta fundamental en matemáticas y tienen propiedades y comportamientos que permiten su estudio y aplicación en diversas áreas. El conocimiento de estos conceptos es fundamental para entender y resolver problemas que involucren series infinitas.
Comparación entre series finitas e infinitas
A lo largo de la matemática, las series han desempeñado un papel fundamental en diversos campos, como el cálculo y la teoría de números. Hay dos tipos principales de series: finitas e infinitas.
Series finitas
Una serie finita es aquella que tiene un número limitado de términos. Por ejemplo, la serie 1 + 2 + 3 + 4 + 5 es finita, ya que tiene un total de cinco términos.
Las series finitas son más fáciles de trabajar y evaluar, ya que podemos sumar todos los términos fácilmente. Además, podemos aplicar diferentes operaciones matemáticas, como restar, multiplicar o dividir, a las series finitas sin problemas.
Series infinitas
Una serie infinita es aquella que tiene un número ilimitado de términos. Por ejemplo, la serie 1 + 1/2 + 1/4 + 1/8 + … es infinita, ya que los términos continúan hasta el infinito.
Las series infinitas son más complejas de trabajar y evaluar, ya que no podemos sumar todos los términos de manera directa. En su lugar, utilizamos conceptos como la convergencia y la divergencia para estudiar el comportamiento de las series infinitas.
En las series infinitas, es importante tener en cuenta el límite de la serie, es decir, hacia dónde tiende la suma de todos los términos. Algunas series infinitas pueden converger hacia un valor finito, mientras que otras pueden divergir hacia el infinito o no tener un valor límite definido.
Las series infinitas tienen aplicaciones prácticas en muchas áreas, como la física y la ingeniería. Por ejemplo, la serie infinita 1/n^2 se utiliza en la teoría de la probabilidad para calcular la suma de las probabilidades de todos los eventos posibles.
Comparación
En resumen, las series finitas tienen un número limitado de términos y son más fáciles de trabajar y evaluar. Por otro lado, las series infinitas tienen un número ilimitado de términos y requieren conceptos más avanzados, como la convergencia y la divergencia, para ser estudiadas.
En conclusión, tanto las series finitas como las series infinitas son importantes en matemáticas y tienen diferentes propiedades y aplicaciones. Ambas tienen su lugar y son fundamentales para el desarrollo de diferentes áreas de estudio y aplicación de la matemática.
En este artículo hemos analizado los principales elementos de etiquetas HTML que se pueden utilizar para resaltar frases importantes en un texto.
Una de las etiquetas que más impacto visual tiene es strong. Esta etiqueta se utiliza para enfatizar una palabra o frase y se muestra en negrita. Es ideal para resaltar información crucial o frases clave en un texto.
Otra opción para resaltar frases importantes es el uso de la etiqueta h3. Esta etiqueta se utiliza para crear un encabezado de tercer nivel y, al ser un título, resalta automáticamente la información que sigue a continuación. Es una buena opción si se desea categorizar y jerarquizar la información en un texto.
Para resaltar una lista de frases importantes, se puede utilizar la etiqueta ul en combinación con la etiqueta li. La etiqueta ul crea una lista desordenada y cada ítem de la lista se define con la etiqueta li. Es una forma efectiva de organizar y resaltar una serie de frases que se desean destacar.
Además de las etiquetas mencionadas, también se puede utilizar la etiqueta b para poner en negrita las frases importantes. Sin embargo, cabe destacar que esta etiqueta no tiene un impacto visual tan fuerte como las etiquetas strong o h3, por lo que se recomienda utilizarlas en su lugar.
En conclusión, disponemos de varias opciones en HTML para resaltar frases importantes en un texto. Se puede utilizar la etiqueta strong, h3, listas en HTML o la etiqueta b. La elección dependerá del nivel de énfasis y visibilidad que se desee dar a la información destacada. Al utilizar estas etiquetas correctamente, se logrará captar la atención del lector y transmitir de manera efectiva el mensaje clave del texto.