Las funciones trigonométricas son fundamentales en las matemáticas y desempeñan un papel crucial en una amplia gama de aplicaciones científicas y tecnológicas. En este artículo, exploraremos las características y la representación gráfica de las funciones trigonométricas más comunes, como el seno, el coseno y la tangente. Comprender estas funciones es esencial para estudiantes de matemáticas y física, así como para profesionales que trabajan en campos como la ingeniería, la astronomía y la arquitectura.
Importancia de las funciones trigonométricas
Las funciones trigonométricas modelan fenómenos periódicos y oscilatorios, como el movimiento de un péndulo, las ondas sonoras y la luz, así como el comportamiento de las señales eléctricas en circuitos. Además, las funciones trigonométricas permiten analizar y predecir patrones en datos, lo que las hace vitales en disciplinas que van desde la estadística hasta la astronomía.
Características de las funciones trigonométricas
Las funciones trigonométricas clave incluyen el seno, el coseno y la tangente, cada una con sus propias propiedades distintivas. Estas funciones exhiben patrones periódicos y recurrentes, lo que les otorga cualidades únicas que las diferencian de otras funciones matemáticas.
Seno (sin)
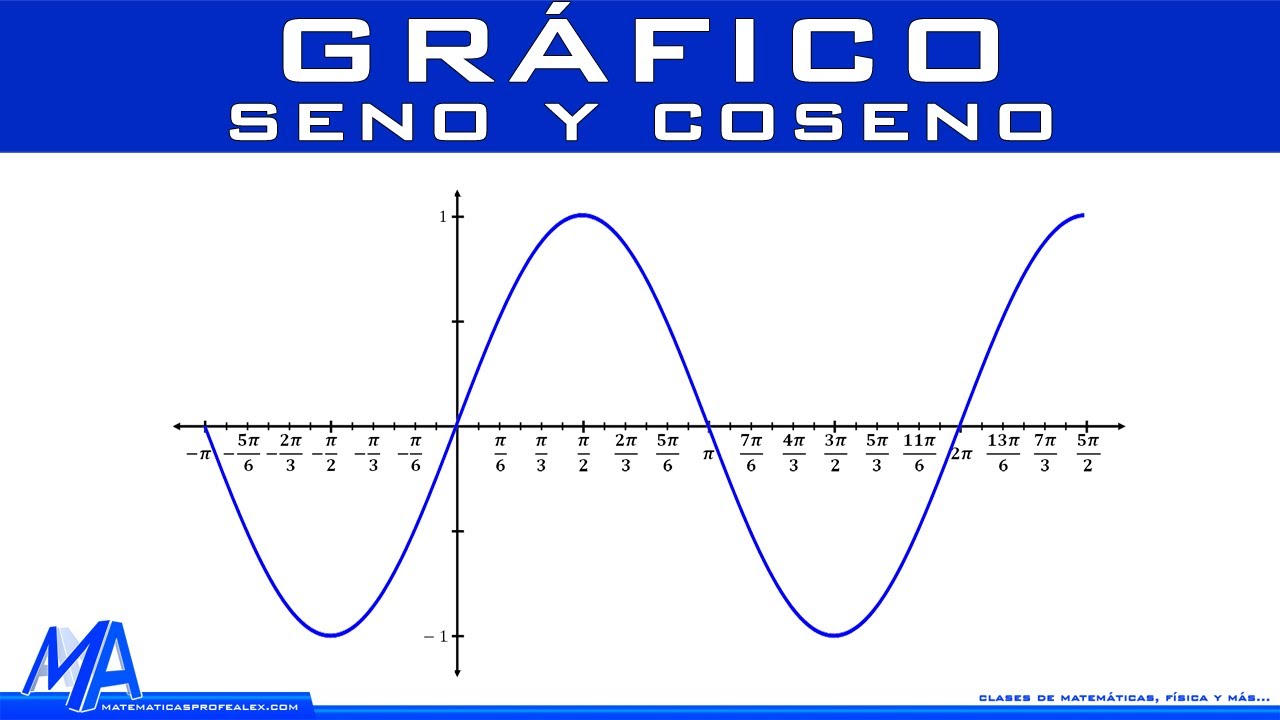
El seno de un ángulo en un triángulo rectángulo es la relación entre la longitud del cateto opuesto y la hipotenusa. En un sentido más general, el seno es una función periódica que oscila entre -1 y 1, con un período de 2π. Su gráfica forma una onda sinusoidal, lo que la hace especialmente útil en el análisis de fenómenos armónicos.
Coseno (cos)
El coseno, al igual que el seno, es una función periódica que oscila entre -1 y 1 con un período de 2π. Sin embargo, su gráfica representa una onda desfasada en π/2 con respecto a la del seno. El coseno es fundamental en el estudio de oscilaciones, fases y desfases en sistemas físicos y mecánicos.
Tangente (tan)
La tangente de un ángulo es la relación entre el seno y el coseno de ese ángulo. La gráfica de la tangente tiene asíntotas en los puntos donde el coseno se anula, lo que la hace especialmente relevante en el análisis de fenómenos que implican divisiones entre estas dos funciones trigonométricas.
Representación gráfica de funciones trigonométricas
Visualizar las funciones trigonométricas mediante representaciones gráficas es esencial para comprender su comportamiento y propiedades. Las gráficas revelan patrones, simetrías, desfases y periodos, entre otras características, que ayudan a interpretar y aplicar estas funciones en contextos reales.
Gráfica del seno
La gráfica del seno es una onda sinusoidal que oscila entre -1 y 1 a medida que varía el ángulo. Esta representación visualiza la periodicidad de la función, así como sus puntos máximos, mínimos, intersecciones con el eje x y su comportamiento asintótico.
Gráfica del coseno
Al igual que la gráfica del seno, la del coseno es una onda sinusoidal. Sin embargo, está desfasada en π/2 con respecto a la del seno, lo que la hace útil para analizar fenómenos con diferentes fases y oscilaciones.
Gráfica de la tangente
La gráfica de la tangente exhibe discontinuidades en los puntos donde el coseno se anula, lo que se refleja en sus asíntotas verticales. Estas características son fundamentales para comprender el comportamiento de la tangente en contextos físicos y matemáticos.
Usos de las funciones trigonométricas en la vida cotidiana
Las funciones trigonométricas se encuentran en numerosas aplicaciones cotidianas, desde el diseño de puentes hasta la creación de efectos visuales en el cine y los videojuegos. Comprender las propiedades y la representación gráfica de estas funciones permite abordar problemas del mundo real con herramientas matemáticas poderosas y elegantes.
Ingeniería y arquitectura
En el diseño y la construcción de estructuras como puentes, rascacielos y edificios, las funciones trigonométricas son esenciales para calcular ángulos, pendientes y dimensiones geométricas. Los ingenieros y arquitectos utilizan estas funciones para modelar el comportamiento de las fuerzas y analizar la estabilidad estructural.
La navegación marítima y la astronomía dependen de las funciones trigonométricas para determinar la posición de estrellas, planetas y otros cuerpos celestes. Los cálculos de coordenadas, distancias y ángulos se basan en conceptos trigonométricos fundamentales.
Computación gráfica y animación
En la industria del entretenimiento, las funciones trigonométricas se utilizan para crear efectos visuales, animaciones y simulaciones realistas. Desde el movimiento de personajes hasta la generación de entornos virtuales, estas funciones son imprescindibles en la creación de contenido digital atractivo y convincente.
Las funciones trigonométricas desempeñan un papel vital en las matemáticas y en numerosos campos de la ciencia y la ingeniería. Su representación gráfica y sus propiedades distintivas las convierten en herramientas poderosas para analizar y modelar fenómenos periódicos y oscilatorios en el mundo real. Comprender y dominar estas funciones es clave para desarrollar habilidades analíticas y aplicadas que son fundamentales en la resolución de problemas complejos en diversos ámbitos.