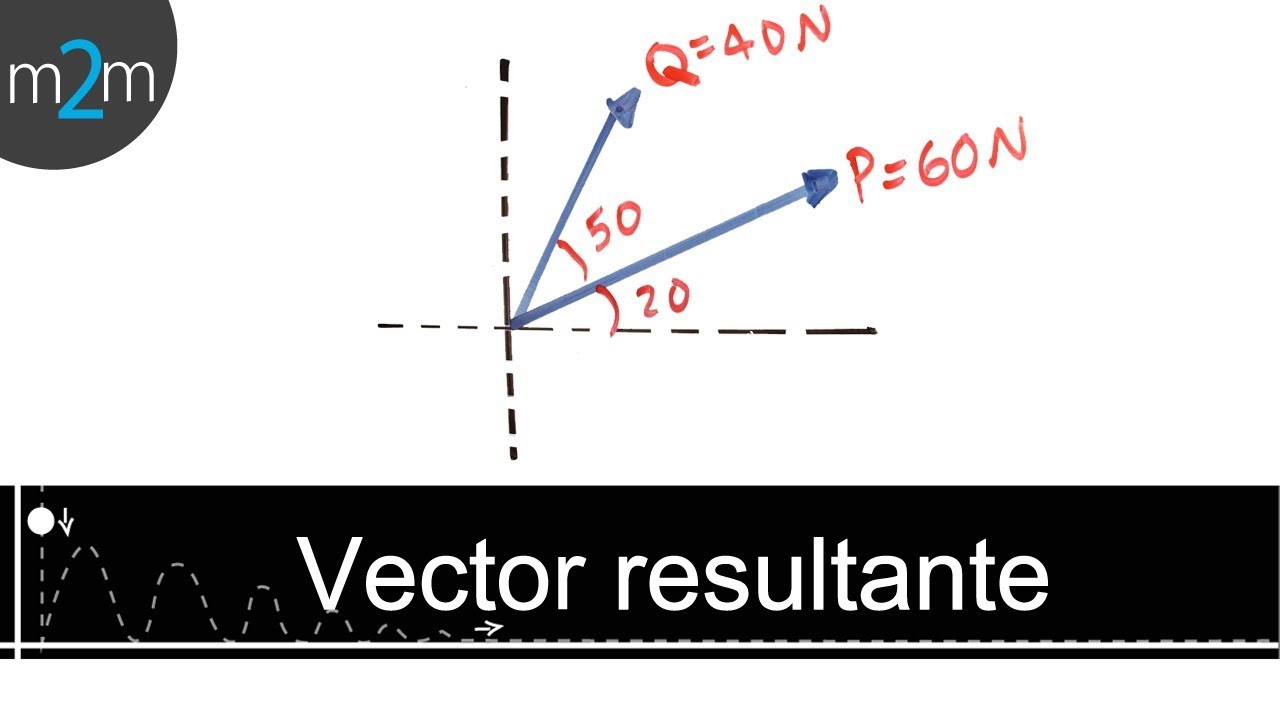
El concepto de resultante de un vector es fundamental en matemáticas y física, ya que nos permite comprender el efecto combinado de múltiples fuerzas o desplazamientos. En este artículo, exploraremos en detalle qué es la resultante de un vector, cómo se calcula y su importancia en diferentes campos de la ciencia y la ingeniería.
¿Qué es un vector?
Antes de adentrarnos en la definición de la resultante de un vector, es crucial tener claridad sobre qué es un vector. En términos simples, un vector es una cantidad que tiene magnitud y dirección. Esto significa que, aparte de indicarnos cuánto (magnitud), también nos dice hacia dónde (dirección). Los vectores se representan gráficamente como flechas, donde la longitud de la flecha representa la magnitud y la dirección de la flecha indica la dirección del vector.
Definición de la resultante de un vector
Cuando tenemos dos o más vectores actuando simultáneamente, la resultante es el vector que representa el efecto total de todos los vectores combinados. En otras palabras, la resultante es el vector que produce el mismo efecto que todos los vectores originales juntos. Este concepto es esencial para comprender cómo actúan diferentes fuerzas o desplazamientos en un sistema.
Adición de vectores
La resultante de dos vectores puede calcularse mediante la adición de los vectores individualmente. Para sumar vectores, podemos utilizar el método del triángulo o el método del paralelogramo. Ambos métodos nos permiten encontrar la resultante de manera precisa, teniendo en cuenta tanto la magnitud como la dirección de los vectores originales.
Componentes rectangulares
En muchos casos, los vectores se presentan en forma de componentes rectangulares, es decir, con cantidades separadas en direcciones perpendiculares (por ejemplo, horizontal y vertical). Para calcular la resultante en estas situaciones, podemos usar las componentes individuales de cada vector para obtener la resultante final. Este enfoque es especialmente útil en problemas de física y ingeniería.
Importancia en la física
La noción de la resultante de un vector es fundamental en la resolución de problemas de mecánica y dinámica. Por ejemplo, al analizar el movimiento de un objeto sometido a múltiples fuerzas, es crucial calcular la resultante de todas las fuerzas para comprender su efecto combinado sobre el objeto. La resultante también se utiliza en el análisis de fuerzas concurrentes y sistemas de fuerzas distribuidas.
Equilibrio de fuerzas
En el contexto de la física, la resultante de un conjunto de fuerzas también nos permite determinar si un objeto está en equilibrio. Si la resultante de todas las fuerzas es cero, el sistema se encuentra en equilibrio, tanto en términos de la translación como de la rotación. Este concepto es fundamental para comprender el comportamiento estático de objetos bajo la influencia de fuerzas exteriores.
Aplicaciones en ingeniería
En el ámbito de la ingeniería, la resultante de un vector es crucial en el diseño y análisis de estructuras, sistemas mecánicos y circuitos eléctricos. Al comprender cómo las fuerzas se combinan para producir efectos resultantes, los ingenieros pueden diseñar soluciones eficientes y seguras para una amplia variedad de aplicaciones.
Análisis de estructuras
En el diseño y la evaluación de estructuras como puentes, edificios y maquinaria, la determinación de las resultantes de fuerzas internas es esencial. Esto permite garantizar que la estructura pueda soportar las cargas esperadas sin exceder sus límites de resistencia. Además, el análisis de las resultantes de fuerzas ayuda a identificar posibles puntos de tensión y optimizar la distribución de materiales.
Optimización de sistemas mecánicos
En el desarrollo de sistemas mecánicos, desde motores hasta sistemas de transporte, comprender la resultante de las fuerzas aplicadas es crucial para garantizar un rendimiento óptimo y una vida útil prolongada. El diseño de dispositivos que minimicen las fuerzas resultantes puede conducir a una mayor eficiencia y durabilidad en una amplia gama de aplicaciones.
En resumen, la resultante de un vector es una herramienta poderosa que nos ayuda a comprender cómo múltiples vectores interactúan para producir un efecto combinado. Tanto en la física como en la ingeniería, la capacidad de calcular la resultante de manera precisa es fundamental para comprender el comportamiento de sistemas complejos y diseñar soluciones efectivas. Al dominar los conceptos relacionados con la resultante de un vector, los profesionales en ciencia e ingeniería pueden abordar desafíos con mayor claridad y precisión.