«`html
Un triángulo rectángulo es una figura geométrica que tiene un ángulo recto, es decir, un ángulo de 90 grados. En este tipo de triángulo, la relación entre la hipotenusa y el cateto opuesto es fundamental para comprender diversas aplicaciones en matemáticas y ciencias. En este artículo, exploraremos en detalle esta relación y su importancia en diferentes contextos.
«`
«`html
Comprendiendo la relación trigonométrica
«`
«`html
La relación entre la hipotenusa y el cateto opuesto en un triángulo rectángulo se basa en los conceptos de trigonometría, que es la rama de las matemáticas que estudia las relaciones entre los ángulos y los lados de un triángulo. En particular, nos enfocaremos en la función trigonométrica seno, que es fundamental para comprender esta relación.
«`
«`html
Para comenzar, consideremos un triángulo rectángulo con un ángulo agudo θ. La hipotenusa es el lado opuesto al ángulo recto, y los otros dos lados son el cateto opuesto (lado que forma el ángulo θ) y el cateto adyacente (lado que forma el ángulo θ con la hipotenusa).
«`
«`html
Definición del seno
«`
«`html
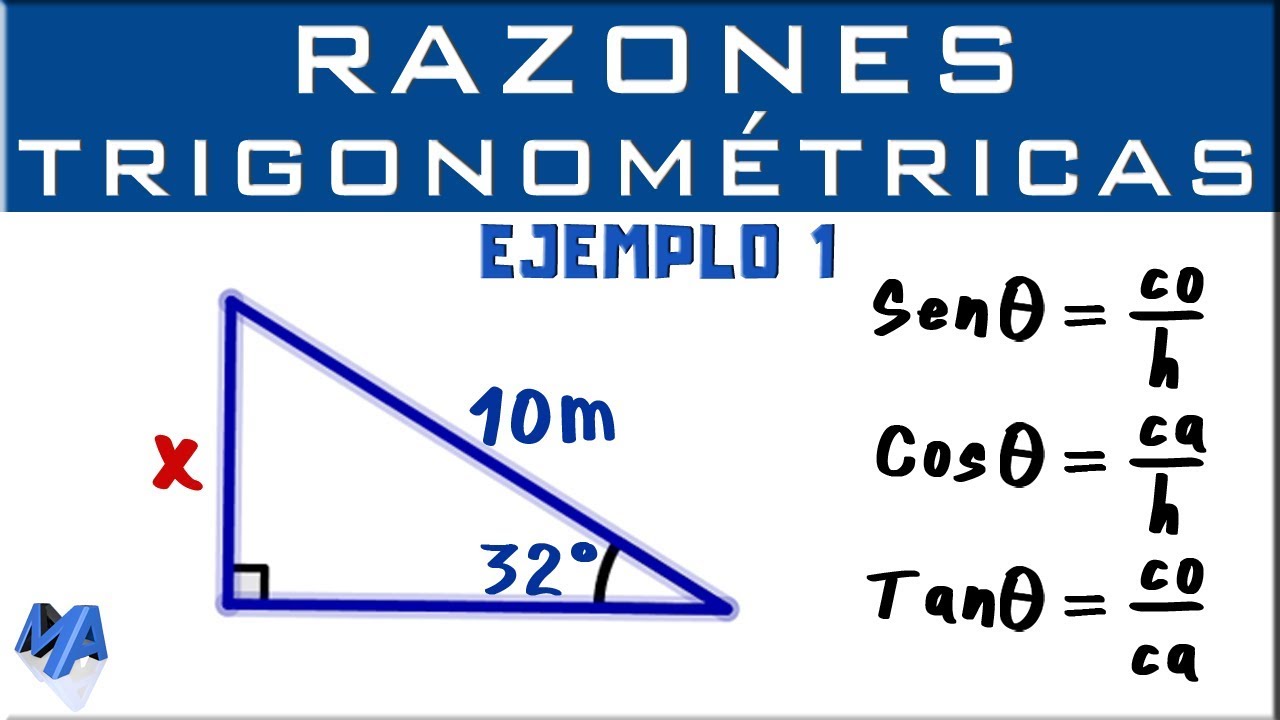
El seno de un ángulo se define como la razón entre el cateto opuesto y la hipotenusa. Matemáticamente, podemos expresar esta relación de la siguiente manera:
«`
«`html
sen(θ) = cateto opuesto / hipotenusa
«`
«`html
Esta definición nos proporciona una base sólida para comprender la relación entre la hipotenusa y el cateto opuesto en un triángulo rectángulo. El seno de un ángulo nos indica cómo varía la longitud del cateto opuesto en relación con la longitud de la hipotenusa a medida que cambia el ángulo.
«`
«`html
Para visualizar esta relación, consideremos un ejemplo simple. Si tenemos un triángulo rectángulo con una hipotenusa de longitud 5 unidades y un cateto opuesto de longitud 3 unidades, podemos calcular el seno del ángulo agudo utilizando la fórmula mencionada anteriormente.
«`
«`html
Aplicaciones en la vida cotidiana
«`
«`html
La comprensión de la relación entre la hipotenusa y el cateto opuesto en un triángulo rectángulo tiene aplicaciones prácticas en diversas áreas. Por ejemplo, en la arquitectura y la construcción, los ingenieros utilizan estos conceptos para calcular la inclinación de techos, la altura de estructuras y la longitud de pendientes. También son fundamentales en campos como la navegación, la ingeniería civil y la física.
«`
«`html
Además, la trigonometría es esencial en la resolución de problemas relacionados con la medición de distancias inaccesibles, como determinar la altura de un árbol o la longitud de un río desde un punto de observación específico. Estos ejemplos ilustran la relevancia práctica de la relación entre la hipotenusa y el cateto opuesto en un triángulo rectángulo en numerosos escenarios del mundo real.
«`
«`html
Relación con otras funciones trigonométricas
«`
«`html
Además del seno, existen otras funciones trigonométricas, como el coseno y la tangente, que también se relacionan con los lados de un triángulo rectángulo. El coseno se define como la razón entre el cateto adyacente y la hipotenusa, mientras que la tangente se define como la razón entre el cateto opuesto y el cateto adyacente.
«`
«`html
Estas funciones trigonométricas son fundamentales para resolver problemas que involucran triángulos rectángulos y tienen diversas aplicaciones en campos como la ingeniería, la astronomía y la geometría computacional. Comprender cómo estas funciones se relacionan con los lados de un triángulo rectángulo amplía nuestras capacidades para resolver problemas complejos en el mundo físico y teórico.
«`
«`html
Desafíos y ejercicios prácticos
«`
«`html
Para fortalecer la comprensión de la relación entre la hipotenusa y el cateto opuesto en un triángulo rectángulo, es beneficioso abordar desafíos y ejercicios prácticos. Resolver problemas que requieran aplicar conceptos trigonométricos en situaciones reales o abstractas ayuda a internalizar y afianzar el conocimiento adquirido.
«`
«`html
Por ejemplo, resolver problemas de medición de alturas, distancias y ángulos utilizando las funciones trigonométricas puede ser una forma efectiva de mejorar las habilidades matemáticas y desarrollar un enfoque analítico para resolver situaciones desafiantes. Además, la resolución de problemas prácticos fomenta la creatividad y el pensamiento crítico.
«`
«`html
Conclusión
«`
«`html
En resumen, la relación entre la hipotenusa y el cateto opuesto en un triángulo rectángulo es un concepto fundamental en trigonometría con amplias aplicaciones en diversos campos. Al comprender esta relación y su significado, los estudiantes y profesionales pueden adquirir habilidades analíticas y prácticas que les permiten abordar desafíos matemáticos y situaciones del mundo real con confianza y precisión.
«`
«`html
Además, la conexión entre la teoría matemática y su aplicación práctica resalta la importancia de la trigonometría en la resolución de problemas reales, desde la construcción de estructuras hasta la exploración espacial. Continuar explorando y ampliando nuestra comprensión de estos conceptos es esencial para el avance y la innovación en numerosos campos científicos y tecnológicos.
«`