Las fracciones son una parte fundamental de las matemáticas, y comprender su representación numérica en términos generales es esencial para desarrollar habilidades matemáticas sólidas. En este artículo, exploraremos detalladamente cómo se representan las fracciones en términos numéricos, brindando una comprensión clara y concisa para aquellos que deseen fortalecer su base en matemáticas.
Fracciones: Una mirada más cercana
Las fracciones son representaciones numéricas de partes de un todo. Se componen de dos números: el numerador, que representa la cantidad de partes consideradas, y el denominador, que representa el número total de partes que componen el todo. Como ejemplo, consideremos la fracción 3/4. Aquí, el numerador es 3, lo que indica que estamos considerando 3 partes de un todo, mientras que el denominador es 4, que representa el total de partes que componen el todo. Ahora, profundicemos en cómo se representan numéricamente las fracciones en términos generales.
Representación Decimal de las Fracciones
Una de las formas más comunes de representar numéricamente una fracción es a través de su equivalente decimal. Para lograr esto, se divide el numerador entre el denominador. Por ejemplo, para la fracción 3/4, dividiríamos 3 entre 4 para obtener 0.75 como resultado. Este proceso nos da una representación decimal de la fracción, lo que facilita su comparación con otros números decimales y su uso en cálculos matemáticos cotidianos.
Importancia de la Representación Decimal
La representación decimal de las fracciones es fundamental en diversas áreas, como la economía, la ingeniería y la ciencia. Al convertir una fracción a su forma decimal, se permite una mayor facilidad en la comparación y el cálculo con otros números decimales. Esta representación numérica es crucial para el análisis de datos y la resolución de problemas en contextos prácticos.
Representación en la Recta Numérica
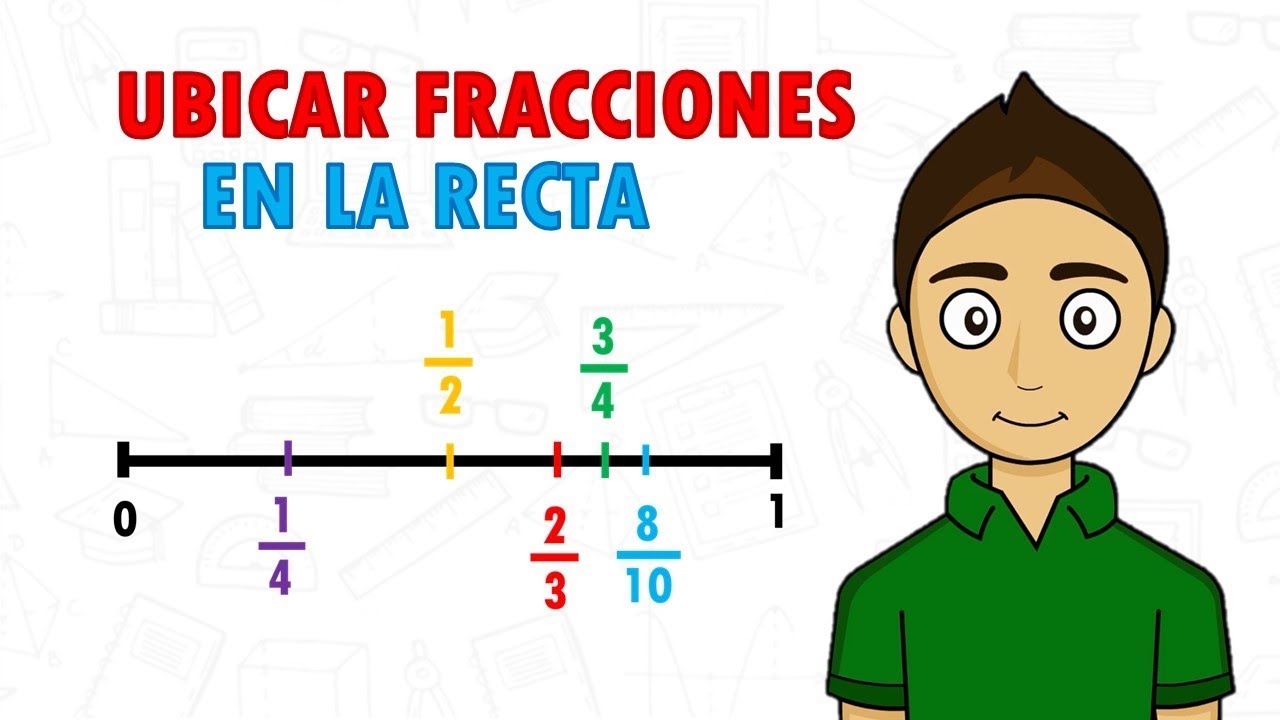
Otra forma visualmente impactante de representar las fracciones en términos generales es a través de la recta numérica. Al trazar una fracción en la recta numérica, se puede visualizar claramente su posición relativa en comparación con otros números. Por ejemplo, la fracción 3/4 estaría ubicada entre el 0 y el 1 en la recta numérica, mostrando claramente su relación con los números enteros y otras fracciones.
Utilidad de la Recta Numérica
La representación de fracciones en la recta numérica es una herramienta invaluable en la comprensión de la relación entre las fracciones y los números enteros. Esta representación gráfica permite a los estudiantes visualizar y comprender mejor cómo se sitúan las fracciones en el contexto de los demás números, lo que contribuye a un entendimiento más profundo de su valor numérico y su utilidad en situaciones cotidianas.
Fracciones Impropias y Mixtas
Además de las fracciones en su forma común, es importante comprender la representación numérica de las fracciones impropias y mixtas. Las fracciones impropias tienen un numerador mayor que su denominador, lo que las hace mayores que 1. Por otro lado, las fracciones mixtas consisten en un número entero junto con una fracción propia. La representación numérica de estas fracciones requiere un enfoque específico para comprender su valor en relación con los números enteros y otras fracciones.
Comparación entre Fracciones Impropias y Mixtas
La representación numérica de fracciones impropias y mixtas presenta desafíos únicos en su comprensión y uso. Es crucial entender cómo estas fracciones se relacionan con los números enteros y cómo se pueden convertir entre sí para facilitar su manipulación en cálculos matemáticos y su interpretación en situaciones prácticas.
Operaciones con Fracciones: Suma y Resta
Una parte fundamental de comprender la representación numérica de las fracciones en términos generales es la habilidad para realizar operaciones matemáticas con ellas. La suma y resta de fracciones requiere un enfoque meticuloso para garantizar resultados precisos y comprender el valor numérico resultante de estas operaciones.
Estrategias para Sumar y Restar Fracciones
Existen diversas estrategias para sumar y restar fracciones, como encontrar un denominador común, convertir fracciones a equivalentes con el mismo denominador y operar con los numeradores. Comprender estas estrategias es crucial para realizar operaciones con fracciones de manera eficiente y precisa, lo que es fundamental en el desarrollo de habilidades matemáticas sólidas.
Operaciones con Fracciones: Multiplicación y División
Además de la suma y resta, la multiplicación y división de fracciones también son áreas clave en su representación numérica en términos generales. Estas operaciones requieren un enfoque específico y la comprensión de cómo afectan el valor numérico de las fracciones involucradas.
Propiedades de la Multiplicación y División de Fracciones
Conocer las propiedades de la multiplicación y división de fracciones es fundamental para comprender cómo estas operaciones afectan el valor numérico de las fracciones. Por ejemplo, al multiplicar fracciones, se multiplican los numeradores entre sí y los denominadores entre sí, lo que puede simplificar la fracción resultante. Del mismo modo, al dividir fracciones, se multiplica la primera fracción por la inversa de la segunda, lo que conduce a una comprensión más profunda de cómo operar con fracciones de manera efectiva.
Aplicaciones Prácticas de las Fracciones
Finalmente, es fundamental comprender cómo se aplican las fracciones en situaciones prácticas, desde la cocina hasta la ingeniería. La representación numérica de las fracciones en términos generales cobra vida en contextos cotidianos, lo que subraya su importancia en el desarrollo de habilidades matemáticas en el mundo real.
Uso de Fracciones en la Vida Diaria
Las fracciones se utilizan ampliamente en la vida diaria, desde medir cantidades en la cocina hasta calcular proporciones en la construcción. Comprender cómo representar numéricamente las fracciones en términos generales es esencial para su aplicación práctica, lo que destaca la relevancia y utilidad de estas habilidades matemáticas en el mundo real.
En conclusión, la representación numérica de las fracciones en términos generales es fundamental para el desarrollo de habilidades matemáticas sólidas. Comprender cómo representar las fracciones en sus equivalentes decimales, en la recta numérica, así como en operaciones matemáticas, y su aplicación en la vida cotidiana, enriquece la comprensión numérica y promueve la capacidad de resolver problemas de manera efectiva. Al dominar la representación numérica de las fracciones, se establece una base sólida para el éxito en matemáticas y su aplicación en diversos ámbitos de la vida.