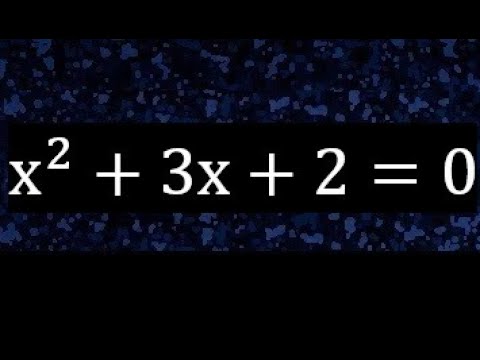Bienvenidos a otro artículo de resolución de ecuaciones. En este post, nos enfocaremos en resolver la ecuación cuadrática x2 – 3x + 2 = 0 paso a paso. Si alguna vez te has sentido confundido por las ecuaciones cuadráticas, ¡no te preocupes! Vamos a desglosar cada paso para que puedas comprender completamente el proceso de resolución.
Desglosando la ecuación
Antes de sumergirnos en la resolución de la ecuación, es crucial comprender cómo está estructurada. La ecuación x2 – 3x + 2 = 0 es una ecuación cuadrática, lo que significa que tiene un término cuadrático (x2), un término lineal (-3x) y una constante (2). Este tipo de ecuaciones puede resolverse utilizando diferentes métodos, y aquí te guiaremos a través de uno de los enfoques más comunes.
Factorización de la ecuación cuadrática
Para resolver la ecuación x2 – 3x + 2 = 0, usaremos el método de factorización. La factorización nos permite descomponer la ecuación en sus factores para encontrar las soluciones para x. El primer paso en el proceso de factorización es identificar dos números que, cuando se suman, den el coeficiente del término lineal (-3) y cuando se multiplican, den el producto del término cuadrático y el término constante (x2*2 = 2).
Encontrando los factores
Para encontrar estos dos números, buscamos un par de factores de la constante (2) que sumen el coeficiente del término lineal (-3). En este caso, los números son -2 y -1, ya que su suma es -3 y su producto es 2. Ahora que hemos encontrado estos factores, los utilizaremos para descomponer el término lineal.
Descomposición de la ecuación
La descomposición de la ecuación implica reescribir el término lineal utilizando los factores que identificamos previamente. Entonces, la ecuación x2 – 3x + 2 = 0 puede expresarse como (x – 2)(x – 1) = 0. Esta forma factoreda nos permite encontrar las soluciones para x al igualar cada factor a cero y resolver para x.
Encontrando las soluciones
Una vez que hemos factorizado la ecuación, podemos proceder a encontrar las soluciones para x. Esto lo logramos igualando cada factor a cero y resolviendo la ecuación resultante para x.
Solución para x = 2
Al igualar el primer factor, x – 2, a cero, obtenemos la ecuación x – 2 = 0. Al resolver para x, encontramos que x = 2. Por lo tanto, 2 es una de las soluciones para nuestra ecuación cuadrática.
Solución para x = 1
Del mismo modo, al igualar el segundo factor, x – 1, a cero, obtenemos la ecuación x – 1 = 0. Resolviendo para x, encontramos que x = 1. Por lo tanto, 1 es la otra solución para nuestra ecuación cuadrática.
Verificación de las soluciones
Es vital verificar nuestras soluciones para asegurarnos de que satisfacen la ecuación original. Podemos hacer esto reemplazando cada solución de x en la ecuación cuadrática x2 – 3x + 2 = 0 y comprobando si obtenemos una igualdad.
Verificando x = 2
Reemplazando x = 2 en la ecuación, obtenemos 22 – 3*2 + 2 = 4 – 6 + 2 = 0. Como el resultado es 0, la solución es válida.
Verificando x = 1
Al reemplazar x = 1 en la ecuación, obtenemos 12 – 3*1 + 2 = 1 – 3 + 2 = 0. Nuevamente, el resultado es 0, lo que confirma que 1 es una solución válida para la ecuación cuadrática.
En conclusión, hemos logrado resolver la ecuación cuadrática x2 – 3x + 2 = 0 utilizando el método de factorización. Al seguir cada paso cuidadosamente, encontramos que las soluciones para x son 2 y 1, las cuales fueron verificadas para satisfacer la ecuación original. Esperamos que este artículo te haya brindado una comprensión clara del proceso de resolución de ecuaciones cuadráticas y te haya ayudado a sentirte más seguro en abordar problemas de este tipo en el futuro.