El cálculo del área bajo la curva es una tarea fundamental en el análisis matemático y la aproximación de esta área es de gran importancia en diversos campos. En este artículo, exploraremos el método de aproximación del área bajo la curva mediante extremos derechos e izquierdos, que es una técnica comúnmente utilizada en cálculo numérico y análisis de datos. Comenzaremos por entender los conceptos fundamentales y luego nos sumergiremos en el proceso paso a paso para aplicar este método de aproximación de manera efectiva.
Conceptos fundamentales del cálculo de área bajo la curva
Antes de adentrarnos en el método de aproximación mediante extremos derechos e izquierdos, es crucial comprender algunos conceptos fundamentales. El cálculo del área bajo la curva implica encontrar el área comprendida entre la curva de una función y el eje x en un intervalo dado. Esta área puede representar la acumulación de cierta magnitud a lo largo de un período de tiempo, el volumen bajo una curva tridimensional, o incluso la probabilidad en el contexto de la teoría de la probabilidad.
Funciones continuas y la aproximación de áreas
En el contexto del método de aproximación mediante extremos derechos e izquierdos, es crucial trabajar con funciones continuas. Una función se considera continua en un intervalo si su gráfico no contiene «saltos» o «huecos». La aproximación del área bajo una curva implica dividir el intervalo dado en subintervalos más pequeños y utilizar métodos específicos para estimar el área en cada subintervalo. Esta aproximación se vuelve más precisa a medida que se incrementa el número de subintervalos.
¿Qué son los extremos derechos e izquierdos?
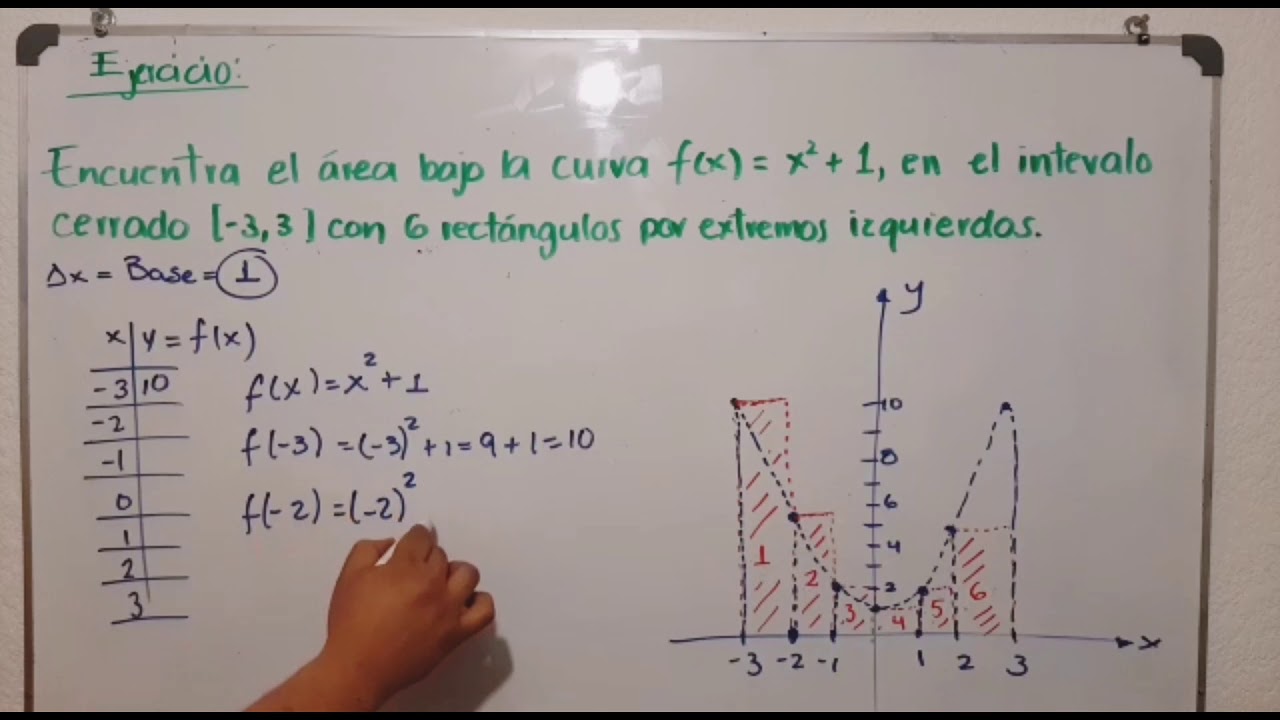
Los extremos derechos e izquierdos son puntos específicos en cada subintervalo que se utilizan para calcular la aproximación del área bajo la curva. En un subintervalo [a, b] dado, el extremo derecho se encuentra en el punto b, mientras que el extremo izquierdo se encuentra en el punto a. Estos extremos se utilizan como referencias para establecer las alturas de los rectángulos que se utilizarán para aproximar el área bajo la curva.
Paso a paso del método de aproximación
División del intervalo
El primer paso en la aplicación del método de aproximación mediante extremos derechos e izquierdos es dividir el intervalo dado en subintervalos más pequeños. Cuanto más pequeños sean los subintervalos, mayor será la precisión de la aproximación. La división del intervalo puede realizarse de manera uniforme o con tamaños de subintervalo variables, dependiendo de la naturaleza de la función y la precisión requerida.
Cálculo de la altura de los rectángulos
Una vez que el intervalo se ha dividido en subintervalos, el siguiente paso implica calcular la altura de los rectángulos que se utilizarán para aproximar el área bajo la curva. Para el extremo derecho de cada subintervalo, la altura del rectángulo corresponde al valor de la función en el extremo derecho, mientras que para el extremo izquierdo, la altura del rectángulo se calcula en base al valor de la función en el extremo izquierdo. Esta altura representa la contribución de cada subintervalo a la aproximación del área.
Suma de las áreas de los rectángulos
Una vez que se han calculado las alturas de los rectángulos en cada subintervalo, el siguiente paso es sumar las áreas de los rectángulos para obtener la aproximación del área bajo la curva en el intervalo dado. Esta suma suele realizarse mediante el método de suma de Riemann, que es una forma efectiva de estimar el área utilizando rectángulos.
Consideraciones adicionales
Precisión y número de subintervalos
La precisión de la aproximación del área bajo la curva mediante extremos derechos e izquierdos está estrechamente relacionada con el número de subintervalos utilizados en el cálculo. A medida que se incrementa el número de subintervalos, la aproximación se vuelve más precisa. Sin embargo, es importante equilibrar esta precisión con la eficiencia computacional, especialmente en situaciones donde se requiere un gran número de cálculos.
Aplicaciones en el análisis numérico
El método de aproximación mediante extremos derechos e izquierdos tiene numerosas aplicaciones en el análisis numérico, especialmente en la resolución de ecuaciones diferenciales y la interpolación de datos. Al utilizar este método, es posible aproximarse a áreas bajo curvas de funciones complejas, lo que facilita el análisis y la interpretación de fenómenos físicos, económicos y sociales.
En resumen, el método de aproximación del área bajo la curva mediante extremos derechos e izquierdos es una herramienta valiosa en el cálculo numérico y el análisis de datos. Al comprender los conceptos fundamentales y seguir el proceso paso a paso, es posible utilizar este método para aproximarse a áreas bajo curvas de manera efectiva. Con su amplia gama de aplicaciones, este método continúa siendo una herramienta relevante en diversos campos de la ciencia y la ingeniería.