Calcular las coordenadas del punto medio de un segmento es una habilidad fundamental en matemáticas. Conocer cómo determinar este punto es crucial para resolver numerosos problemas en geometría y álgebra. En este artículo, aprenderás paso a paso cómo calcular con precisión las coordenadas del punto medio de un segmento, lo que te brindará una base sólida para abordar problemas más complejos y aplicaciones en el mundo real.
Antes de sumergirnos en los detalles del cálculo del punto medio de un segmento, es importante entender la importancia de esta noción en diversas áreas de las matemáticas. El punto medio de un segmento no solo es crucial en geometría, sino que también tiene aplicaciones importantes en física, ingeniería y otras disciplinas científicas.
**
Entendiendo el concepto de punto medio
**
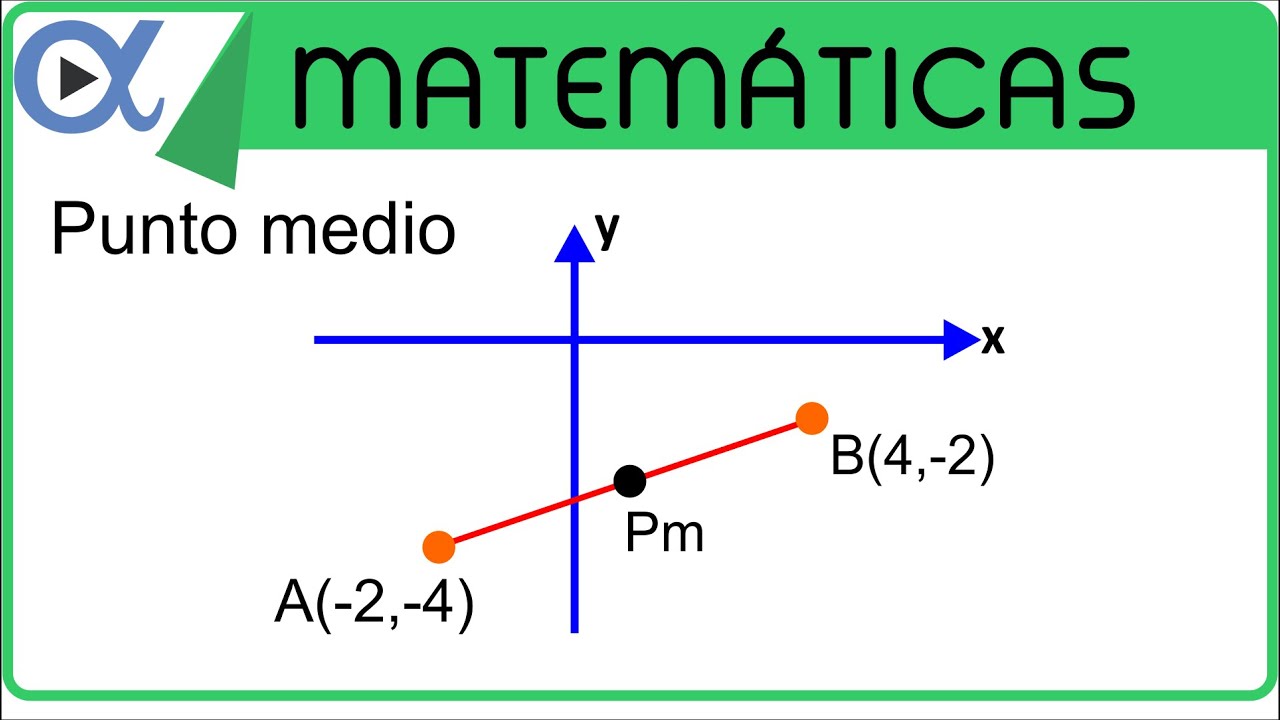
El punto medio de un segmento es simplemente el punto que está exactamente a mitad de camino entre los extremos del segmento. En otras palabras, si tienes un segmento de línea que va desde el punto A al punto B, el punto medio de ese segmento es el punto que se encuentra equidistante de A y B.
**
Fórmula para calcular el punto medio de un segmento
**
Para calcular las coordenadas del punto medio de un segmento, podemos utilizar una fórmula sencilla que nos permitirá encontrar este punto de manera eficiente. La fórmula es la siguiente: ( (x1 + x2) / 2 , (y1 + y2) / 2 ), donde (x1, y1) y (x2, y2) son las coordenadas de los extremos del segmento.
**
Primer paso: Identificar las coordenadas de los extremos del segmento
**
El primer paso para calcular el punto medio de un segmento es identificar las coordenadas de los extremos del segmento. Si tenemos un segmento con los extremos A(x1, y1) y B(x2, y2), estas son las coordenadas que necesitaremos para aplicar la fórmula del punto medio.
**
Segundo paso: Aplicar la fórmula del punto medio
**
Una vez que tenemos las coordenadas de los extremos del segmento, podemos aplicar la fórmula del punto medio para calcular las coordenadas del punto medio. Simplemente sustituimos las coordenadas de los extremos en la fórmula ( (x1 + x2) / 2 , (y1 + y2) / 2 ) y realizamos las operaciones necesarias.
**
Ejemplo práctico
**
Para comprender mejor cómo se aplica la fórmula del punto medio, consideremos el siguiente ejemplo. Tenemos un segmento con extremos A(2, 4) y B(6, 10). ¿Cuáles son las coordenadas del punto medio de este segmento?
**
Identificar las coordenadas de los extremos
**
En este caso, las coordenadas de los extremos del segmento son A(2, 4) y B(6, 10).
**
Aplicar la fórmula del punto medio
**
Aplicando la fórmula del punto medio: ( (2 + 6) / 2 , (4 + 10) / 2 ) = (4, 7). Por lo tanto, las coordenadas del punto medio de este segmento son (4, 7).
**
Propiedades del punto medio
**
El punto medio de un segmento tiene algunas propiedades interesantes que vale la pena mencionar. Por ejemplo, el punto medio es el centro de simetría del segmento, lo que significa que si trazamos una recta desde cualquier punto del segmento hasta el punto medio, esta recta será bisectada en el punto medio.
Además, el punto medio también divide el segmento en dos segmentos de igual longitud. Esto significa que la distancia desde el punto medio hasta cualquiera de los extremos del segmento es la mitad de la longitud del segmento completo.
**
Aplicaciones en la vida real
**
Aunque el cálculo del punto medio puede parecer un ejercicio puramente académico, tiene aplicaciones muy prácticas en la vida real. Por ejemplo, en física y geometría aplicada, el concepto de punto medio es fundamental para comprender la distribución de cargas, la estabilidad de estructuras y la geometría de objetos físicos.
En ingeniería, el cálculo del punto medio es esencial para diseñar sistemas de distribución de peso, diseño de puentes y estructuras, y en la planificación de rutas y redes de transporte.
**
Conclusiones
**
Calcular las coordenadas del punto medio de un segmento es una habilidad matemática fundamental con numerosas aplicaciones en diversos campos. Al comprender el concepto de punto medio y saber cómo aplicar la fórmula para calcularlo, podemos resolver problemas de geometría, física, ingeniería y otras disciplinas de manera efectiva y precisa.
Además, el punto medio tiene propiedades interesantes que lo hacen relevante en situaciones de simetría y equidistancia, lo que lo convierte en una herramienta poderosa para el análisis y la resolución de problemas prácticos. Con una comprensión sólida del cálculo del punto medio, estamos mejor equipados para enfrentar desafíos matemáticos y aplicaciones del mundo real.