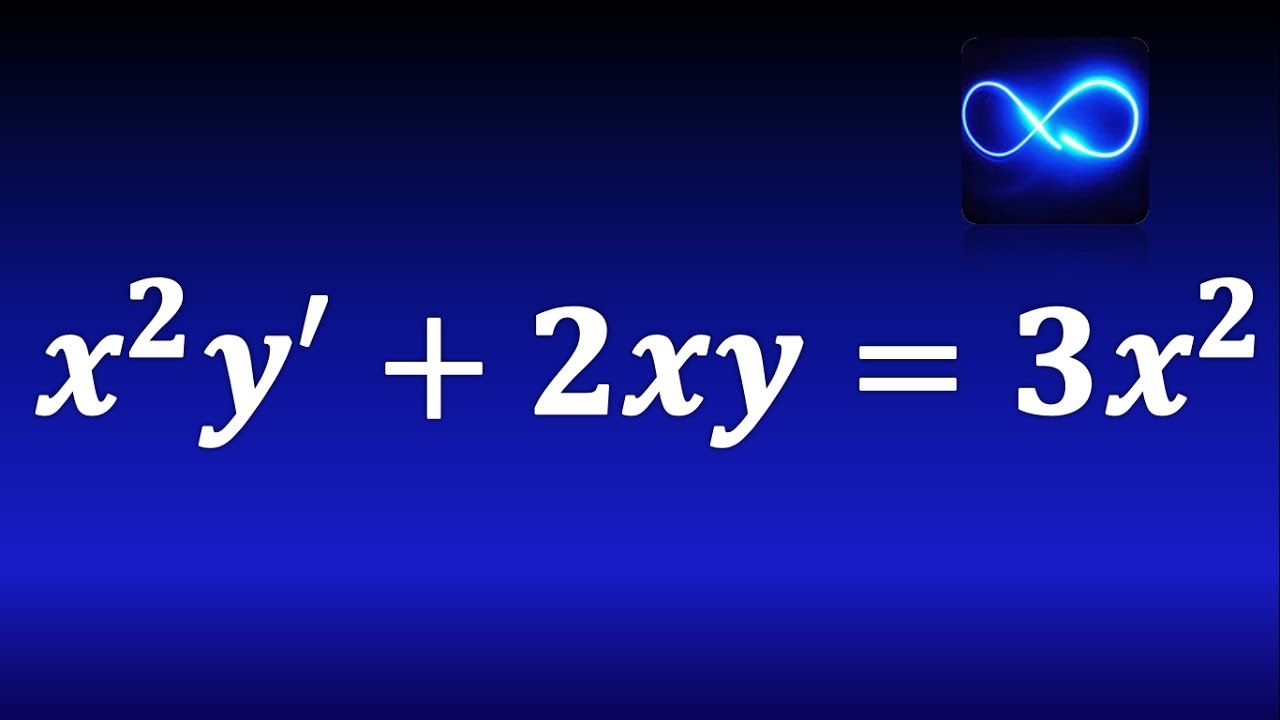Las ecuaciones diferenciales son fundamentales en el campo de las matemáticas y la física, ya que modelan fenómenos de cambio y variación en una amplia gama de situaciones. En este artículo, nos enfocaremos en las ecuaciones diferenciales lineales de primer orden con términos mixtos, explorando su naturaleza, resolviéndolas paso a paso y analizando su aplicación en problemas del mundo real.
Conceptos Básicos
Antes de sumergirnos en el mundo de las ecuaciones diferenciales lineales de primer orden con términos mixtos, es crucial comprender algunos conceptos fundamentales. En su forma más simple, una ecuación diferencial es una expresión que relaciona una función desconocida con sus derivadas. Las ecuaciones diferenciales lineales se caracterizan por ser aquellas en las que la función desconocida y sus derivadas aparecen en forma lineal, es decir, no se multiplican ni se dividen entre sí mismas. Por otro lado, las ecuaciones de primer orden involucran únicamente la primera derivada de la función desconocida.
Cómo Identificar una Ecuación Diferencial Lineal de Primer Orden con Términos Mixtos
Para abordar con éxito la resolución de este tipo particular de ecuaciones diferenciales, es esencial entender cómo identificarlas. Una ecuación diferencial lineal de primer orden con términos mixtos se puede reconocer por su forma general, que incluye la función desconocida, sus derivadas de diferentes órdenes y posiblemente términos no derivados. Estas ecuaciones pueden presentar una combinación de términos lineales y no lineales, lo que las hace desafiantes pero a la vez fascinantes de resolver.
Pasos para Resolver una Ecuación Diferencial Lineal de Primer Orden con Términos Mixtos
Resolver una ecuación diferencial de primer orden con términos mixtos requiere paciencia, atención al detalle y un enfoque metódico. A continuación, presentamos los pasos a seguir para abordar este tipo de ecuaciones de manera sistemática:
Paso 1: Identificar la Ecuación Diferencial
El primer paso consiste en identificar correctamente la ecuación diferencial en cuestión, asegurándose de que esté escrita en su forma estándar y que todos los términos estén claramente definidos. Este paso es fundamental para evitar confusiones más adelante en el proceso de resolución.
Paso 2: Clasificar la Ecuación
Una vez que la ecuación diferencial ha sido identificada, es importante clasificarla para determinar el enfoque de resolución apropiado. Las ecuaciones diferenciales lineales se clasifican según la naturaleza de sus coeficientes y términos, lo que proporciona pistas importantes sobre el método más efectivo a emplear.
Paso 3: Multiplicador Integrante (si es necesario)
En algunos casos, la ecuación diferencial puede requerir el uso de un multiplicador integrante para simplificar su forma y facilitar el proceso de resolución. Esta técnica es especialmente útil cuando se manejan términos mixtos que complican la integración directa.
Paso 4: Integración de la Ecuación
Una vez que la ecuación se ha simplificado en la medida de lo posible, el siguiente paso implica la integración de ambas partes de la ecuación para obtener la solución general. Este proceso puede implicar el uso de diferentes técnicas de integración dependiendo de la naturaleza de los términos presentes en la ecuación.
Paso 5: Aplicar Condiciones Iniciales (si es necesario)
En el caso de problemas con valores iniciales específicos, es crucial aplicar estas condiciones a la solución general obtenida para determinar las constantes de integración y obtener así la solución particular que cumple con las condiciones dadas.
Aplicaciones Prácticas
Aunque el proceso de resolver ecuaciones diferenciales lineales de primer orden con términos mixtos puede parecer abstracto, su aplicación se extiende a numerosas áreas del mundo real. Se utilizan para modelar sistemas dinámicos en física, biología, economía y muchas otras disciplinas, proporcionando una herramienta poderosa para comprender y predecir el comportamiento de fenómenos complejos.
En resumen, el estudio de las ecuaciones diferenciales lineales de primer orden con términos mixtos es fundamental para aquellos que buscan comprender el papel crucial que desempeñan en la descripción de procesos de cambio. Al seguir los pasos mencionados y comprender su aplicación en contextos prácticos, es posible dominar la resolución de estas ecuaciones y apreciar su versatilidad en la modelización de situaciones del mundo real.