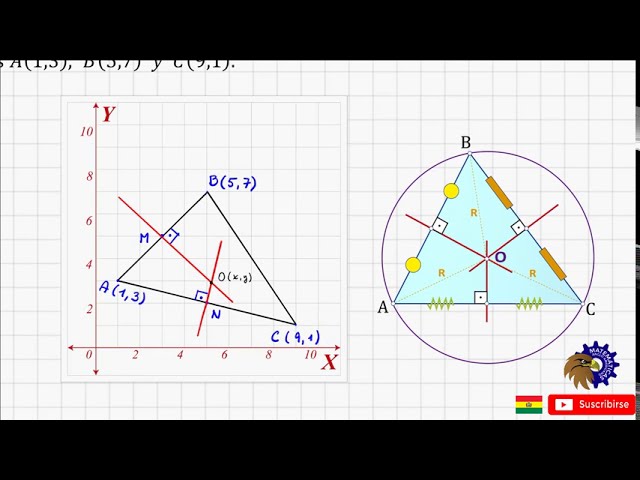
En geometría, el punto de intersección de las tres mediatrices de un triángulo es un concepto fundamental que tiene implicaciones importantes en la geometría euclidiana. Las mediatrices de un triángulo son segmentos de líneas que conectan cada vértice de un triángulo con el punto medio del lado opuesto, y el punto de intersección de estas mediatrices tiene propiedades únicas y significativas.
Propiedades del Punto de Intersección
El punto de intersección de las tres mediatrices de un triángulo, comúnmente conocido como el circuncentro, se encuentra equidistante de los tres vértices del triángulo. Esta propiedad es fundamental, ya que demuestra que el circuncentro es el centro de la circunferencia circunscrita al triángulo, lo que tiene importantes implicaciones en la resolución de problemas geométricos y en la construcción de figuras.
Construcción del Circuncentro
Para encontrar el circuncentro de un triángulo, se trazan las mediatrices de al menos dos lados del triángulo. La intersección de estas mediatrices es el circuncentro. Este proceso puede realizarse utilizando regla y compás, lo que demuestra la importancia histórica y práctica de este concepto en la geometría clásica.
Relación con el Circuncentro
El punto de intersección de las mediatrices también está estrechamente relacionado con el circuncentro en términos de su definición y propiedades. Ambos conceptos se refieren al mismo punto en un triángulo, lo que resalta la importancia y la multiplicidad de enfoques para comprender la geometría de las figuras triangulares.
Aplicaciones en Geometría Euclidiana
El punto de intersección de las mediatrices tiene aplicaciones significativas en geometría euclidiana, ya que proporciona una base para resolver problemas relacionados con la circunferencia circunscrita y la triangulación de puntos en un plano. Estas aplicaciones son fundamentales en diversos campos, desde la cartografía hasta la navegación marítima.
Teorema de la Existencia
El teorema de la existencia del punto de intersección de las mediatrices afirma que, para cualquier triángulo dado, existe un único punto que satisface las propiedades de ser equidistante a los vértices. Este teorema es fundamental en la demostración matemática y la formalización de la geometría de los triángulos.
Relación con el Centroide y Ortocentro
El punto de intersección de las mediatrices también está relacionado con el centroide y el ortocentro de un triángulo. Estos puntos notables tienen propiedades geométricas y métricas que se entrelazan de manera interesante, lo que demuestra la complejidad y belleza de la geometría de los triángulos.
Construcción Geométrica
La construcción geométrica del punto de intersección de las mediatrices es una actividad educativa poderosa que permite a los estudiantes comprender visualmente la relación entre los diferentes elementos de un triángulo. Esta construcción fomenta el pensamiento crítico y el razonamiento espacial en un entorno educativo.
Relación con el Teorema de la Bisectriz
La relación entre el punto de intersección de las mediatrices y el teorema de la bisectriz demuestra la conectividad de diversos conceptos en la geometría de los triángulos. Al explorar esta relación, los estudiantes pueden profundizar su comprensión de las propiedades fundamentales de los triángulos y sus aplicaciones en diversos contextos matemáticos.
Implicaciones en la Resolución de Problemas
El conocimiento del punto de intersección de las mediatrices es crucial para la resolución de problemas geométricos que involucran las relaciones métricas y angulares de un triángulo. Esta comprensión permite simplificar la resolución de problemas complejos y fomenta el desarrollo de habilidades matemáticas avanzadas.
Aplicaciones Prácticas en Ingeniería y Arquitectura
En la ingeniería y arquitectura, el punto de intersección de las mediatrices se utiliza en el diseño y la construcción de estructuras, ya que proporciona una base para el cálculo preciso de distancias y ángulos en la disposición de elementos triangulares. Esta aplicación demuestra la relevancia y utilidad práctica de la geometría euclidiana en campos técnicos y creativos.
Relación con la Teoría de Fractales
En la teoría de fractales, el punto de intersección de las mediatrices tiene conexiones interesantes con la geometría auto-similar y la estructura fractal de ciertos conjuntos geométricos. Estas conexiones muestran la profundidad y amplitud de las implicaciones matemáticas del punto de intersección de las mediatrices en múltiples disciplinas.
Conclusión
En conclusión, el punto de intersección de las tres mediatrices de un triángulo es un concepto crucial en la geometría euclidiana, con aplicaciones significativas en matemáticas, ciencia, y diversos campos de la ingeniería y la tecnología. Su papel en la construcción geométrica, resolución de problemas y aplicaciones prácticas demuestra la importancia de comprender este concepto en profundidad.