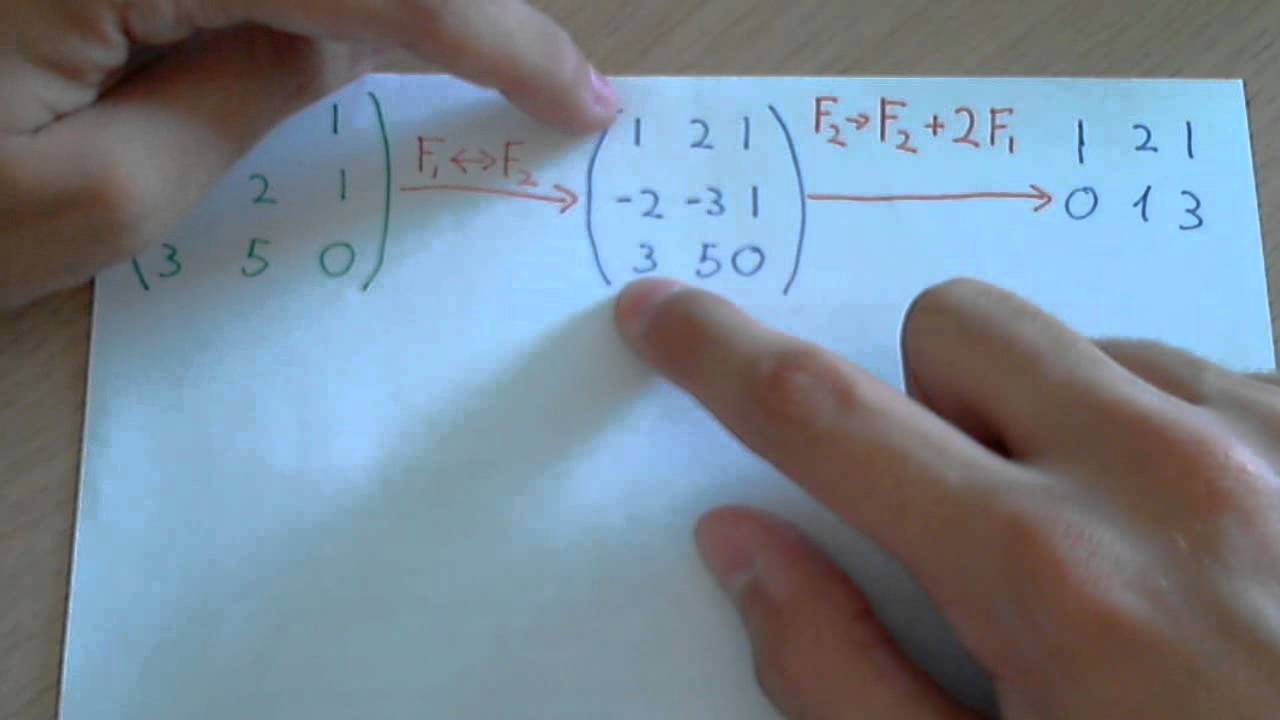Transformaciones elementales por renglón
Las transformaciones elementales por renglón son operaciones fundamentales en la teoría de matrices. Estas transformaciones permiten modificar una matriz mediante operaciones básicas que preservan las propiedades de la matriz original.
Ejemplos de transformaciones elementales por renglón:
- Intercambio de renglones: Consiste en intercambiar la posición de dos renglones de una matriz.
- Multiplicación de un renglón por una constante: Consiste en multiplicar cada elemento de un renglón de una matriz por una constante no nula.
- Suma de un múltiplo de un renglón a otro renglón: Consiste en sumar a un renglón de una matriz el producto de una constante no nula y otro renglón.
Estas transformaciones se utilizan en diversos contextos, como en la resolución de sistemas de ecuaciones lineales, diagonalización de matrices y en operaciones de reducción de matrices.
Es importante destacar que las transformaciones elementales por renglón no afectan al determinante de una matriz y conservan la equivalencia entre sistemas de ecuaciones lineales.
Escalonamiento de una matriz
El escalonamiento de una matriz es un procedimiento que se utiliza en el álgebra lineal para simplificar una matriz y facilitar su resolución. Consiste en aplicar una serie de operaciones elementales a las filas de la matriz hasta que esta adquiera una forma escalonada.
Para entender mejor este concepto, vamos a ver un ejemplo. Supongamos que tenemos la siguiente matriz:
1 2 1 3
2 3 -1 1
3 1 2 4
4 2 3 -1
El primer paso en el escalonamiento de esta matriz es asegurarnos de que el primer elemento de la primera fila sea diferente de cero (si no lo es, intercambiamos filas). En este caso, el primer elemento de la primera fila es 1, por lo que no es necesario hacer ningún intercambio.
A continuación, vamos a hacer cero los elementos debajo del primer elemento de la primera fila. Para lograr esto, multiplicamos la primera fila por los coeficientes necesarios y los restamos de las filas siguientes:
Paso 1:
1 2 1 3 0 -1 -3 -5 0 -5 -1 -5 0 -6 -2 -7
En este caso, multiplicamos la primera fila por -2 y la restamos de la segunda fila; luego, multiplicamos la primera fila por -3 y restamos el resultado de la tercera fila; por último, multiplicamos la primera fila por -4 y restamos el resultado de la cuarta fila.
Ahora, repetimos este proceso con la segunda fila. Primero, asegurándonos de que el segundo elemento de la segunda fila sea diferente de cero:
Paso 2:
1 2 1 3 0 -1 -3 -5 0 0 14 25 0 0 10 17
En este caso, multiplicamos la segunda fila por -7 y la restamos de la tercera fila; luego, multiplicamos la segunda fila por -5 y restamos el resultado de la cuarta fila.
Continuamos con el tercer paso, haciendo cero los elementos debajo del segundo elemento de la segunda fila:
Paso 3:
1 2 1 3 0 -1 -3 -5 0 0 14 25 0 0 0 27
Finalmente, hacemos cero los elementos debajo del tercer elemento de la tercera fila:
Paso 4:
1 2 1 3 0 -1 -3 -5 0 0 14 25 0 0 0 27
Obtenemos así una matriz escalonada, la cual facilita la resolución de sistemas de ecuaciones lineales y otros problemas matemáticos. Este método también es útil para determinar el rango de una matriz y encontrar sus espacios nulo y columna.
En resumen, el escalonamiento de una matriz es un procedimiento que simplifica la matriz y facilita su análisis y resolución. Consiste en aplicar una serie de operaciones elementales a las filas de la matriz hasta que esta adquiera una forma escalonada.
Núcleo de una matriz
El núcleo de una matriz es uno de los conceptos más importantes en el ámbito de las matrices. Se refiere al conjunto de vectores que están en el espacio nulo de la matriz, es decir, aquellos vectores que al multiplicarse por la matriz dan como resultado el vector cero.
Para encontrar el núcleo de una matriz, podemos utilizar técnicas de álgebra lineal y cálculo matricial. Generalmente, se busca un conjunto de vectores que cumpla con la condición de que al multiplicarse por la matriz, se obtenga el vector cero.
Para expresar de manera matemática el núcleo de una matriz A, podemos utilizar la notación N(A). Esto nos indica que estamos hablando del espacio nulo de la matriz A.
Es importante destacar que el núcleo de una matriz puede ser un conjunto vacío si la matriz es de rango completo, es decir, si no existen vectores que al multiplicarse por la matriz den como resultado el vector cero. En este caso, decimos que la matriz es de rango completo o de rango máximo.
En resumen, el núcleo de una matriz es el conjunto de vectores que al multiplicarse por la matriz dan como resultado el vector cero. Es un concepto fundamental en álgebra lineal y tiene diversas aplicaciones en áreas como la física, la ingeniería y la computación.
Rango de una matriz
El rango de una matriz es una medida de su dimensionalidad o grado de libertad. En términos sencillos, se refiere al número máximo de columnas o filas linealmente independientes que tiene la matriz.
Para calcular el rango de una matriz, se pueden utilizar diferentes métodos, como la eliminación gaussiana, la descomposición en valores singulares o la factorización QR. Estos métodos ayudan a reducir la matriz a una forma más simple y determinar su rango con mayor facilidad.
En la teoría de matrices, es común utilizar la terminología de «espacios de fila» y «espacios de columna» para describir el rango de una matriz. El espacio de fila se refiere al espacio vectorial generado por las filas de la matriz, mientras que el espacio de columna se refiere al espacio vectorial generado por las columnas.
El rango de una matriz se puede determinar contando el número de vectores linealmente independientes en el espacio de columna o de fila. Por ejemplo, si una matriz tiene tres vectores linealmente independientes en su espacio de columna, su rango será 3.
Es importante destacar que el rango de una matriz no puede ser mayor que el número de filas o columnas de la matriz. Si una matriz tiene más filas que columnas, su rango máximo será igual al número de columnas; si tiene más columnas que filas, su rango máximo será igual al número de filas.
El rango de una matriz es una propiedad importante que puede tener aplicaciones en diversas áreas, como la resolución de sistemas de ecuaciones lineales, la teoría de grafos, la compresión de datos y el análisis de redes.
En conclusión, el uso de etiquetas HTML es una herramienta efectiva para resaltar las frases más importantes de un texto.
Al utilizar la etiqueta , se le otorga énfasis visual a esas frases, lo que ayuda a captar la atención del lector y resaltar la información clave. Esto es especialmente útil en párrafos largos donde se desea destacar una idea relevante.
Además del uso de , también se pueden utilizar encabezados HTML
para separar secciones importantes del texto. Estos encabezados facilitan la navegación y facilitan la comprensión de la estructura general del contenido.
Por otro lado, las listas en HTML son una excelente manera de presentar información de manera organizada y concisa. Al combinar listas y , se puede resaltar aún más los puntos clave dentro de cada elemento de la lista.
En resumen, el uso de etiquetas HTML permite resaltar frases importantes, los encabezados HTML
ayudan a estructurar el contenido y las listas en HTML proporcionan una forma ordenada de presentar información. Estas técnicas son útiles para mejorar la legibilidad y comprensión del texto por parte del lector.