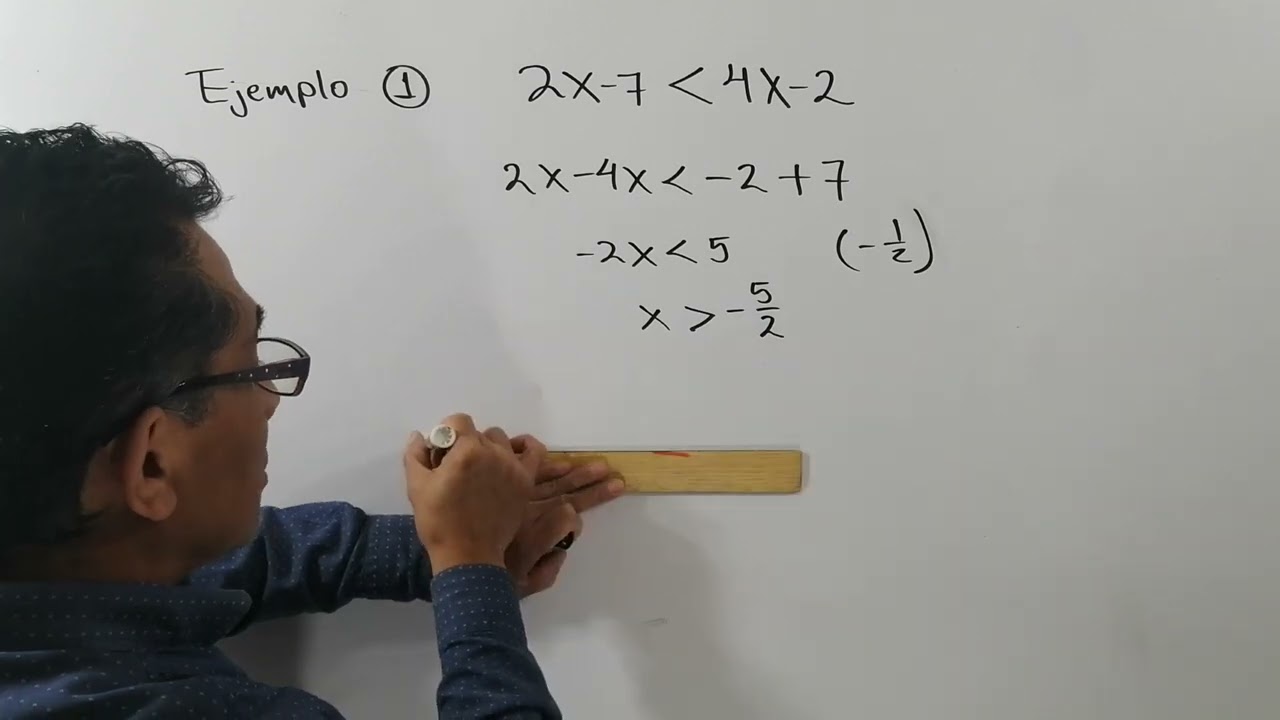¿Qué es la desigualdad en cálculo diferencial?
Una desigualdad en cálculo diferencial es una expresión matemática que establece una relación de comparación entre dos cantidades. A diferencia de una igualdad, donde ambas cantidades son exactamente iguales, en una desigualdad se establece que una cantidad es mayor, menor o diferente que la otra.
Existen diferentes tipos de desigualdades en cálculo diferencial, como las desigualdades estrictas donde se utiliza el símbolo «» para indicar que una cantidad es estrictamente mayor o menor que la otra. Por ejemplo:
5x + 3 > 2x – 1
Esta desigualdad indica que el valor de «x» que cumple con esta expresión debe ser mayor que -2.
También existen las desigualdades no estrictas, donde se utiliza el símbolo «=» para indicar que una cantidad es mayor o igual, o menor o igual que la otra. Por ejemplo:
2x + 4 <= x + 9
Esta desigualdad indica que el valor de «x» que cumple con esta expresión puede ser mayor o igual a 5.
En cálculo diferencial, las desigualdades son utilizadas para establecer los intervalos en los que una función es positiva, negativa, creciente o decreciente. Estas desigualdades son útiles para determinar el comportamiento de una función en un intervalo dado y para encontrar los puntos críticos, donde la función cambia de signo o alcanza sus máximos y mínimos.
En resumen, la desigualdad en cálculo diferencial es una herramienta matemática que permite establecer relaciones de comparación entre cantidades y se utiliza para delimitar los intervalos en los que una función cumple determinadas condiciones.
Características de las desigualdades en cálculo diferencial
En el cálculo diferencial, las desigualdades juegan un papel fundamental y presentan ciertas características importantes que debemos conocer. A continuación, mencionaremos algunas de ellas:
Intervalos
Las desigualdades en cálculo diferencial se representan mediante intervalos. Estos intervalos pueden ser abiertos, cerrados, semiabiertos o infinitos, y nos permiten describir conjuntos de valores que satisfacen una determinada desigualdad.
Manipulación de desigualdades
En cálculo diferencial, podemos manipular desigualdades de manera similar a las ecuaciones. Podemos sumar, restar, multiplicar o dividir ambos lados de la desigualdad por una constante o una función. Sin embargo, debemos tener cuidado al realizar estas operaciones, ya que algunas desigualdades pueden cambiar de sentido al multiplicar o dividir por números negativos.
Solución de desigualdades
Para resolver desigualdades en cálculo diferencial, debemos identificar los valores que satisfacen la desigualdad. Esto se puede hacer mediante el uso de gráficas, tablas de valores o técnicas algebraicas. Es importante recordar que la solución de una desigualdad puede ser un conjunto de valores, y no solo un número específico.
Propiedades de las desigualdades
Las desigualdades en cálculo diferencial también tienen propiedades importantes. Por ejemplo, podemos aplicar la propiedad transitiva para comparar desigualdades y determinar si una es mayor, menor o igual a otra. También podemos aplicar la propiedad de la suma o multiplicación para simplificar desigualdades y encontrar intervalos de solución.
En resumen, las desigualdades en cálculo diferencial son representadas mediante intervalos y pueden ser manipuladas y resueltas de manera similar a las ecuaciones. Es importante tener en cuenta las propiedades de las desigualdades al realizar operaciones y determinar la solución de una desigualdad.
Uso de desigualdades en problemas de optimización
En problemas de optimización, el uso de desigualdades es fundamental para encontrar la mejor solución. Las desigualdades nos permiten establecer restricciones que deben cumplirse para obtener el máximo o mínimo valor de una función objetivo.
Por ejemplo, si estamos buscando maximizar la producción de una fábrica, podríamos establecer una desigualdad que indique que la cantidad producida debe ser mayor o igual a un valor mínimo. De esta manera, restringimos las posibles soluciones a aquellas que cumplan con dicha condición.
Además, las desigualdades nos brindan la posibilidad de modelar diferentes situaciones y tomar decisiones óptimas en base a las restricciones establecidas. Por ejemplo, si estamos planeando la distribución de recursos en una empresa, podemos utilizar desigualdades para limitar la cantidad de recursos asignados a cada departamento.
En la resolución de problemas de optimización, es común utilizar técnicas como la programación lineal, donde las desigualdades se representan mediante restricciones lineales. Estas restricciones se pueden expresar en forma de ecuaciones y desigualdades, y luego se busca la combinación óptima que maximice o minimice la función objetivo.
En resumen, el uso de desigualdades en problemas de optimización nos permite establecer restricciones y modelar diferentes situaciones. Estas restricciones nos ayudan a encontrar la mejor solución en base a las condiciones establecidas. La programación lineal es una técnica comúnmente utilizada para resolver este tipo de problemas.
Propiedades de las desigualdades en cálculo diferencial
En cálculo diferencial, las desigualdades son una herramienta fundamental para comparar y analizar funciones. A continuación, se presentan algunas propiedades importantes de las desigualdades en este contexto:
Propiedad de adición
Si en una desigualdad se suma o resta el mismo número a ambos lados, el sentido de la desigualdad no cambia. Por ejemplo, si a < b es una desigualdad, entonces a + c < b + c y a – c < b – c también lo son.
Propiedad de multiplicación
Si en una desigualdad se multiplica o divide ambos lados por un número positivo, el sentido de la desigualdad no cambia. Por ejemplo, si a < b es una desigualdad y c es un número positivo, entonces ac < bc y a/c < b/c también lo son.
Propiedad de multiplicación por un número negativo
Si en una desigualdad se multiplica o divide ambos lados por un número negativo, el sentido de la desigualdad cambia. Por ejemplo, si a < b es una desigualdad y c es un número negativo, entonces ac > bc y a/c > b/c también lo son.
Propiedad de transposición
Si en una desigualdad se intercambian los lados, el sentido de la desigualdad cambia. Por ejemplo, si a < b es una desigualdad, entonces b > a también lo es.
Propiedad de reflexividad
Toda expresión relacionada consigo misma es verdadera. Por ejemplo, a > a y b < b siempre son ciertas.
Estas propiedades son fundamentales para manipular y resolver desigualdades en cálculo diferencial. Además, es importante tener en cuenta las restricciones y el dominio de las variables involucradas para garantizar la validez de las desigualdades.
Ejemplos de desigualdades en cálculo diferencial
En el cálculo diferencial, existen diversas desigualdades que son fundamentales para el estudio de las funciones y sus propiedades. A continuación, presentamos cinco ejemplos de desigualdades comunes en este campo:
Ejemplo 1: Desigualdad del valor absoluto
La desigualdad del valor absoluto establece que para cualquier número real a, se cumple que |a| > 0, excepto cuando a = 0. Esto implica que el valor absoluto de un número siempre es positivo, excepto cuando el número es cero.
Ejemplo 2: Desigualdad de la media aritmética y la media armónica
Para cualquier conjunto de números reales positivos x1, x2, …, xn, se cumple que (x1 + x2 + … + xn)/n ≥ n/(1/x1 + 1/x2 + … + 1/xn). Esta desigualdad establece que la media aritmética de un conjunto de números es siempre mayor o igual que la media armónica correspondiente.
Ejemplo 3: Desigualdad de Cauchy-Schwarz
La desigualdad de Cauchy-Schwarz establece que para cualquier par de vectores a = (a1, a2, …, an) y b = (b1, b2, …, bn) en un espacio euclidiano, se cumple que |a · b| ≤ ||a|| ||b||, donde a · b es el producto escalar entre los vectores y ||a|| y ||b|| son las normas de los vectores, respectivamente.
Ejemplo 4: Desigualdad de Bernoulli
La desigualdad de Bernoulli establece que para cualquier número real x ≥ -1 y cualquier número natural n, se cumple que (1 + x)n ≥ 1 + nx. Esta desigualdad es útil en el estudio de crecimiento de funciones y aproximaciones numéricas.
Ejemplo 5: Desigualdad de la media geométrica y la media aritmética
Para cualquier conjunto de números reales positivos x1, x2, …, xn, se cumple que (x1 x2 … xn)1/n ≥ (x1 + x2 + … + xn)/n. Esta desigualdad establece que la media geométrica de un conjunto de números es siempre mayor o igual que la media aritmética correspondiente.
Estos ejemplos de desigualdades en cálculo diferencial son solo una muestra de la importancia que tienen en el análisis matemático y en múltiples aplicaciones en diversas áreas científicas y tecnológicas.