¿Qué es la distancia focal de una elipse?
La distancia focal de una elipse es un concepto fundamental en la geometría de las elipses. Una elipse es una curva cerrada que se forma cuando se corta un cono oblicuamente. Tiene dos ejes principales, el eje mayor y el eje menor. El eje mayor es la distancia más larga entre los extremos de la elipse, mientras que el eje menor es la distancia más corta.
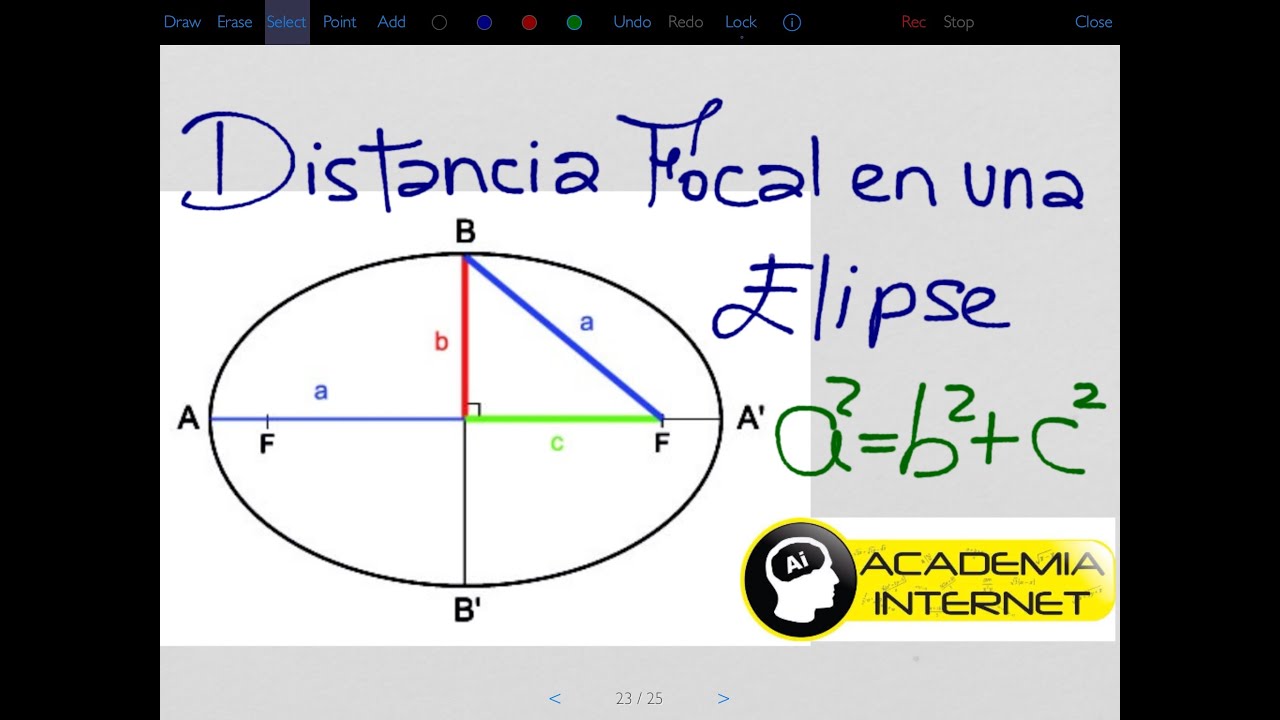
La distancia focal de una elipse se define como la distancia entre el centro de la elipse y uno de los dos focos. Un foco es un punto en la elipse donde la suma de las distancias a cualquier punto de la curva es constante. En otras palabras, cualquier rayo que se refleje en la elipse pasará por uno de los dos focos.
La relación entre los ejes principales y la distancia focal de una elipse está determinada por una fórmula matemática. La fórmula establece que la suma de las distancias desde cualquier punto de la elipse a los dos focos es constante y igual a la longitud del eje mayor.
La distancia focal es importante en muchos campos, como la óptica y la astronomía. En óptica, la distancia focal se utiliza para describir las propiedades de las lentes y los espejos. En astronomía, la distancia focal de un telescopio determina su capacidad para enfocar objetos distantes.
Cálculo de la distancia focal de una elipse
En este artículo, vamos a hablar sobre cómo calcular la distancia focal de una elipse. La distancia focal es un concepto importante en la geometría de las elipses, ya que determina la posición de los focos de la elipse.
Para calcular la distancia focal de una elipse, primero necesitamos conocer la longitud de los ejes mayor y menor de la elipse. Estos valores se denotan como «a» y «b», respectivamente.
Una vez que tenemos los valores de «a» y «b», podemos calcular la distancia focal utilizando la siguiente fórmula:
c = √(a² – b²)
Donde «c» representa la distancia focal.
Por ejemplo, si tenemos una elipse con un eje mayor de longitud 6 y un eje menor de longitud 4, podemos calcular la distancia focal de la siguiente manera:
c = √(6² – 4²) = √(36 – 16) = √20 ≈ 4.47
Entonces, la distancia focal de esta elipse es de aproximadamente 4.47 unidades.
Es importante tener en cuenta que la distancia focal siempre es menor que el eje mayor de la elipse. Además, los puntos focales se encuentran a lo largo del eje mayor y están equidistantes del centro de la elipse.
En resumen, la distancia focal de una elipse se puede calcular utilizando la fórmula c = √(a² – b²), donde «c» representa la distancia focal, y «a» y «b» representan los ejes mayor y menor de la elipse, respectivamente. La distancia focal siempre es menor que el eje mayor de la elipse y los puntos focales se encuentran a lo largo del eje mayor y están equidistantes del centro de la elipse.
Propiedades de la distancia focal en el estudio de las elipses
En el estudio de las elipses, la distancia focal juega un papel fundamental. Es una medida que nos ayuda a entender la forma y características de estas curvas geométricas.
La distancia focal se define como la distancia entre el centro de la elipse y uno de los focos. Se representa con la letra «c». En una elipse, siempre existen dos focos, ubicados en el eje mayor de la figura.
Una de las propiedades más importantes de la distancia focal es que determina la excentricidad de la elipse. La excentricidad es una medida de cuán alargada está la elipse. Cuanto mayor sea la distancia focal en comparación con la longitud del eje mayor, más alargada será la elipse.
En este sentido, podemos decir que la distancia focal y la excentricidad están directamente relacionadas. A medida que la distancia focal aumenta, la elipse se vuelve cada vez más alargada. Por el contrario, si la distancia focal disminuye, la elipse será más cercana a un círculo perfecto, con una excentricidad cercana a cero.
Otra propiedad relevante de la distancia focal es su relación con las órbitas planetarias. En el ámbito astronómico, las órbitas de los planetas alrededor del Sol se describen como elipses. En este contexto, la distancia focal representa la distancia media entre el planeta y el Sol. Esta propiedad es fundamental en la comprensión de las leyes de Kepler y en la predicción del movimiento de los planetas.
En resumen, la distancia focal en el estudio de las elipses es una medida importante que nos ayuda a comprender la forma, excentricidad y características de estas curvas geométricas. Además, tiene una relevancia significativa en el ámbito astronómico, especialmente en el estudio de las órbitas planetarias.
Ejemplos prácticos de cálculo de distancia focal en elipses
En este artículo vamos a ver algunos ejemplos prácticos para calcular la distancia focal en elipses. La distancia focal es un parámetro importante en la geometría de las elipses y nos permite determinar la ubicación del punto focal, que es de donde se origina la radiación de los rayos que inciden en la elipse.
Ejemplo 1: Supongamos que tenemos una elipse con semieje mayor de longitud a=6 y semieje menor de longitud b=4. Para calcular la distancia focal, utilizamos la fórmula c = √(a² – b²), donde c es la distancia focal. Sustituyendo los valores, obtenemos c = √(36 – 16) = √20 = 4.47.
Ejemplo 2: Ahora consideremos una elipse con semieje mayor de longitud a=8 y semieje menor de longitud b=3. Utilizando la misma fórmula c = √(a² – b²), obtenemos c = √(64 – 9) = √55 = 7.42.
Ejemplo 3: Para nuestro último ejemplo, supongamos una elipse con semieje mayor de longitud a=10 y semieje menor de longitud b=6. Aplicando la fórmula c = √(a² – b²), encontramos c = √(100 – 36) = √64 = 8.
Estos ejemplos nos muestran cómo calcular la distancia focal en elipses utilizando la fórmula c = √(a² – b²). Recuerda que la distancia focal es un parámetro fundamental para comprender la geometría de las elipses y su aplicabilidad en diferentes contextos.
Aplicaciones de la distancia focal de una elipse en la vida cotidiana
La elipse es una figura geométrica que tiene múltiples aplicaciones en la vida cotidiana. Una de las propiedades más interesantes de la elipse es su distancia focal, que se define como la distancia entre uno de los focos de la elipse y cualquier punto de la curva.
1. Óptica: La distancia focal de una elipse es utilizada en la óptica para construir lentes de tipo elíptico. Estos lentes se utilizan en telescopios, microscopios y cámaras fotográficas, entre otros dispositivos, para enfocar la luz y formar imágenes nítidas.
2. Acústica: En el campo de la acústica, la distancia focal de una elipse se utiliza para diseñar sistemas de sonido que enfocan el sonido en una dirección específica. Esto es especialmente útil en espacios grandes como teatros o estadios, donde se desea que el sonido llegue a una audiencia específica sin dispersarse demasiado.
3. Comunicaciones: La distancia focal de una elipse también se utiliza en las antenas parabólicas utilizadas para transmisiones de radio y televisión. Estas antenas concentran las ondas electromagnéticas para mejorar la calidad de la señal y reducir las interferencias.
4. Arquitectura: La distancia focal de una elipse es utilizada en la arquitectura para diseñar diseños de edificios con formas curvas, como cúpulas elípticas. Estas estructuras son estéticamente atractivas y también pueden ofrecer beneficios estructurales, como una mayor resistencia al viento.
5. Astronomía: En astronomía, la distancia focal de una elipse se utiliza para calcular la órbita de los planetas y otros objetos celestes. El estudio de las elipses y sus distancias focales es fundamental para comprender el movimiento de los cuerpos celestes en el espacio.
En conclusión, la distancia focal de una elipse tiene muchas aplicaciones prácticas en diferentes campos de la vida cotidiana. Desde la óptica y la acústica hasta la arquitectura y la astronomía, comprender y aprovechar las propiedades de la elipse puede llevar a avances significativos en estas áreas.