El plano cartesiano es una herramienta fundamental en matemáticas para representar gráficamente las relaciones entre variables. En este artículo, te guiaré paso a paso sobre cómo obtener las coordenadas de un plano cartesiano, desde entender los ejes hasta graficar puntos. ¡Sigue leyendo para dominar esta habilidad esencial!
Entendiendo el plano cartesiano
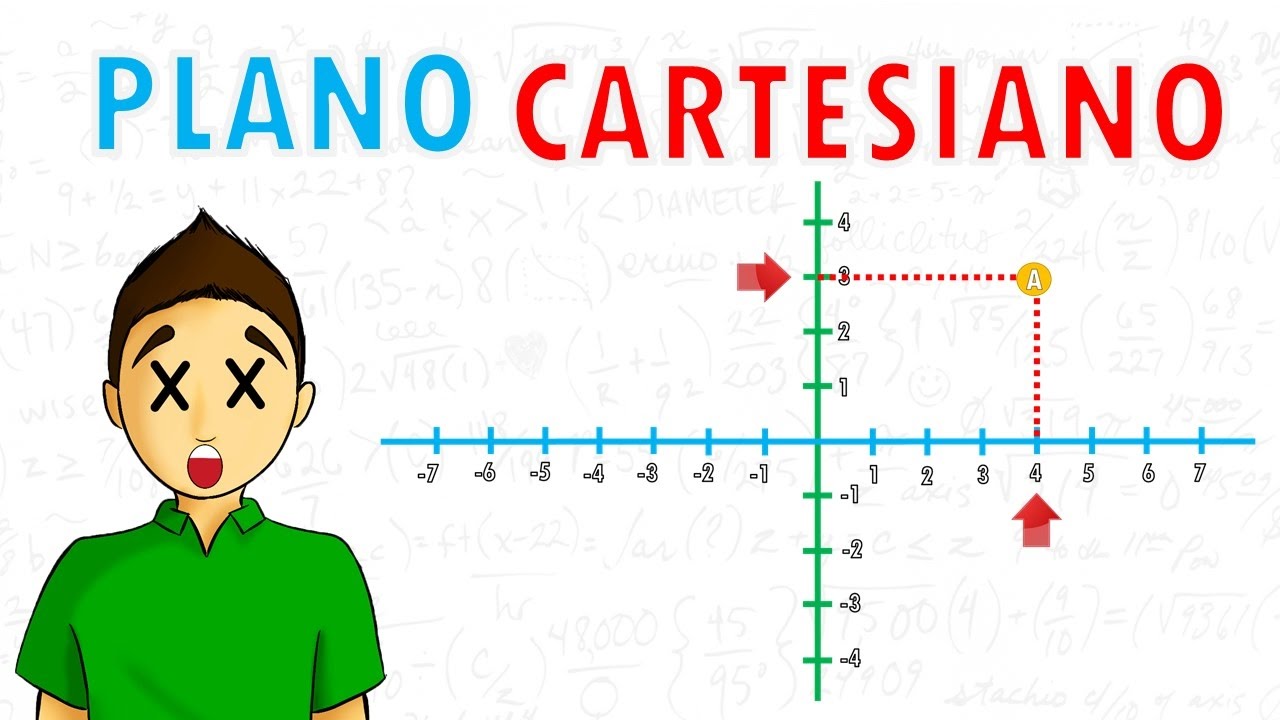
El plano cartesiano consta de dos ejes perpendiculares: el eje x, que se extiende horizontalmente, y el eje y, que se extiende verticalmente. Estos ejes se intersecan en el punto (0,0), conocido como el origen. Las coordenadas de un punto en el plano cartesiano se representan como (x, y), donde x es la distancia horizontal desde el eje y, y y es la distancia vertical desde el eje x.
Localizando el origen
Antes de graficar cualquier punto en el plano cartesiano, es crucial entender la ubicación del origen. El punto (0,0) es el cruce de los dos ejes y sirve como punto de referencia para todas las demás coordenadas. Asegúrate de visualizar este punto como el punto de partida antes de continuar.
Identificando los ejes
El eje x se extiende horizontalmente a lo largo del plano, mientras que el eje y se extiende verticalmente. Es importante comprender la dirección y la orientación de cada eje para poder interpretar correctamente las coordenadas de cualquier punto en el plano cartesiano. Visualiza mentalmente cómo se extienden estos ejes para una mejor comprensión.
Graficando puntos
Una vez que tienes claro el origen y la orientación de los ejes, puedes graficar puntos en el plano cartesiano. Por ejemplo, el punto (2,3) se ubicaría 2 unidades a la derecha del origen en el eje x, y luego 3 unidades hacia arriba en el eje y. Practica graficar varios puntos para familiarizarte con este proceso.
Identificando cuadrantes
El plano cartesiano está dividido en cuatro cuadrantes. El primer cuadrante se encuentra en la parte superior derecha, el segundo cuadrante en la parte superior izquierda, el tercer cuadrante en la parte inferior izquierda y el cuarto cuadrante en la parte inferior derecha. Identificar en qué cuadrante se encuentra un punto es esencial para comprender su posición relativa en el plano.
Calculando la pendiente
La pendiente es una medida de la inclinación de una línea en el plano cartesiano. Se calcula como el cambio en y dividido por el cambio en x entre dos puntos en la línea. Dominar el cálculo de la pendiente te permitirá comprender la relación entre diferentes puntos en el plano cartesiano.
Dibujando líneas
Una vez que comprendes cómo graficar puntos y calcular la pendiente, puedes dibujar líneas rectas entre diferentes puntos en el plano cartesiano. Este proceso te ayudará a visualizar la relación entre diferentes variables representadas por las coordenadas de los puntos.
Entendiendo la intersección de líneas
La intersección de dos líneas en el plano cartesiano puede proporcionar información valiosa sobre la relación entre dos variables. Al comprender cómo identificar y analizar la intersección de líneas, podrás interpretar gráficos con mayor precisión.
Explorando la simetría
La simetría es una propiedad importante en el plano cartesiano. Puedes identificar la simetría respecto al eje x, al eje y o al origen. Comprender la simetría te ayudará a visualizar patrones y relaciones entre diferentes puntos y líneas en el plano.
Graficando funciones
Las funciones matemáticas se representan comúnmente en el plano cartesiano. Aprende a graficar estas funciones al comprender cómo traducir una expresión matemática en un gráfico en el plano cartesiano. Esto te permitirá visualizar y analizar el comportamiento de diferentes funciones.
Identificando puntos especiales
En el plano cartesiano, existen puntos especiales que poseen propiedades distintivas, como el punto medio entre dos puntos o el punto donde una función corta el eje x o y. Identificar y comprender la importancia de estos puntos te permitirá realizar análisis más detallados de los gráficos.
Explorando coordenadas tridimensionales
Aunque el plano cartesiano tradicional es bidimensional, es posible expandir su concepto para trabajar con coordenadas tridimensionales. Explora cómo representar puntos y líneas en un sistema de coordenadas tridimensional para comprender visualmente relaciones espaciales más complejas.
Comprendiendo la representación vectorial
El concepto de vectores es fundamental en matemáticas y física. Aprende cómo representar vectores en el plano cartesiano utilizando coordenadas y cómo realizar operaciones vectoriales básicas, como la suma y la resta de vectores.
Resolviendo problemas del mundo real
Finalmente, aplica tus habilidades en la interpretación del plano cartesiano para resolver problemas del mundo real. Desde analizar datos hasta comprender fenómenos físicos, la capacidad de trabajar con coordenadas en el plano cartesiano es invaluable en una amplia gama de contextos.