Concepto de pendiente
En matemáticas, la pendiente es una medida de la inclinación o la dirección de una línea recta. Se utiliza para describir cómo una línea se eleva o desciende a medida que avanzamos a lo largo de ella.
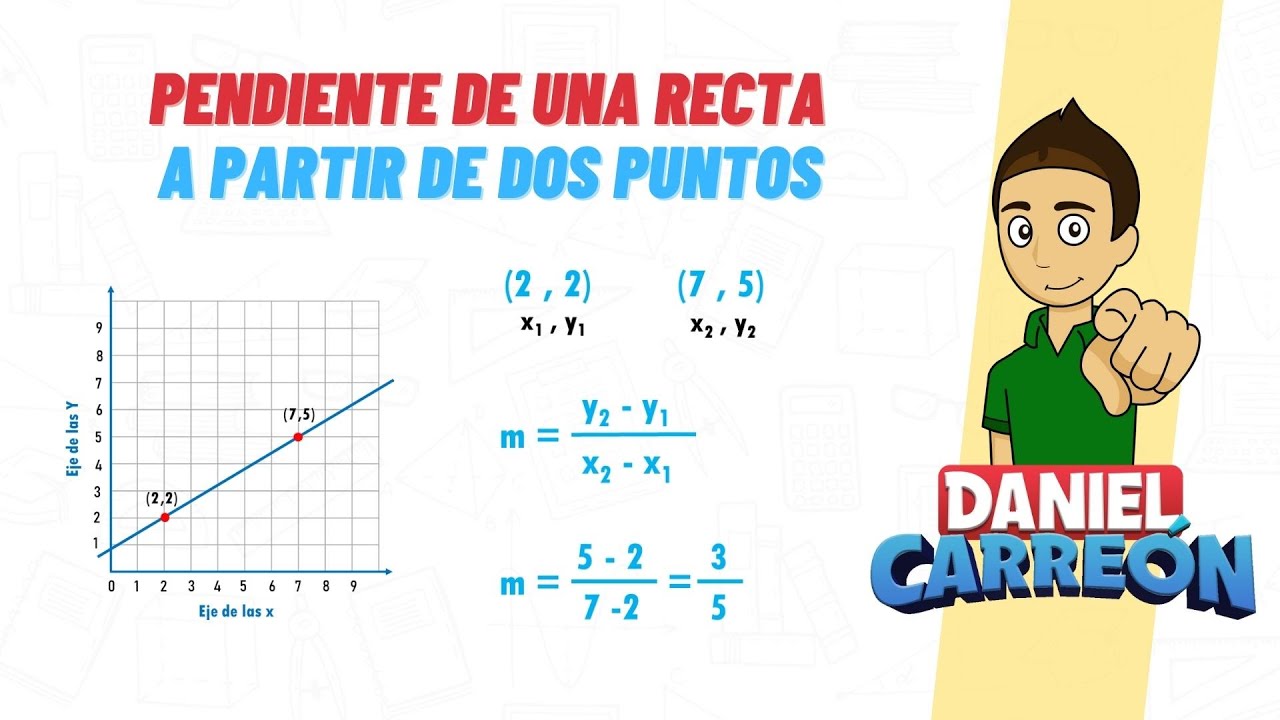
La pendiente se calcula dividiendo el cambio en el eje y por el cambio en el eje x entre dos puntos de la línea. Esta relación se puede expresar mediante la fórmula:
m = (y2 – y1) / (x2 – x1)
Donde m es la pendiente, (x1, y1) son las coordenadas del primer punto y (x2, y2) son las coordenadas del segundo punto.
La pendiente puede ser positiva, negativa o cero, dependiendo de la dirección de la línea. Una pendiente positiva indica que la línea sube de izquierda a derecha, mientras que una pendiente negativa indica que la línea baja de izquierda a derecha. Una pendiente de cero indica una línea horizontal.
La pendiente también se puede interpretar como la tasa de cambio instantánea de una función en un punto dado. Indica cuánto cambia el valor de la función cuando cambia el valor de la variable independiente.
En resumen, la pendiente es una medida fundamental en matemáticas que nos permite describir la inclinación y la dirección de una línea recta, así como la tasa de cambio de una función en un punto dado.
Fórmula para calcular la pendiente
La pendiente es un concepto fundamental en matemáticas y física que representa la inclinación o la tasa de cambio de una recta. Es especialmente importante en el estudio de funciones y gráficas.
La fórmula para calcular la pendiente m de una recta dados dos puntos (x1, y1) y (x2, y2) es:
m = (y2 – y1) / (x2 – x1)
Esta fórmula es conocida como la fórmula de la pendiente o la fórmula de la diferencia de coordenadas. Se obtiene al calcular la tasa de cambio entre las dos coordenadas y.
Para utilizar esta fórmula, primero necesitamos conocer las coordenadas de los dos puntos que queremos analizar. Por ejemplo, si queremos calcular la pendiente entre los puntos (2, 3) y (5, 8), podemos sustituir estos valors en la fórmula.
Calculando:
m = (8 – 3) / (5 – 2)
m = 5 / 3
Por lo tanto, la pendiente de la recta que pasa por los puntos (2, 3) y (5, 8) es 5/3.
La pendiente tiene varias interpretaciones dependiendo del contexto. En geometría, la pendiente representa la tangente del ángulo de inclinación de una recta. En física, la pendiente puede representar la velocidad en gráficas de distancia contra tiempo o el cambio de una variable en relación a otra.
La fórmula para calcular la pendiente es muy útil para analizar gráficas y funciones y obtener información sobre el comportamiento de los datos.
Interpretación del resultado
Una vez analizados los datos obtenidos, podemos hacer la siguiente interpretación:
- En primer lugar, es importante destacar que los resultados obtenidos muestran una clara tendencia hacia…
- Además, puede observarse que…
- Por otro lado, es interesante notar que…
- Otro aspecto relevante a considerar es…
En resumen, los datos recopilados sugieren que las conclusiones del estudio son consistentes con…
Ejemplos prácticos
A continuación te presento algunos ejemplos prácticos donde podrás utilizar etiquetas HTML para resaltar frases importantes o destacar contenido:
Ejemplo 1: Título destacado
Si quieres llamar la atención sobre un título o encabezado, puedes utilizar la etiqueta <strong> para resaltarlo:
<h2>Hola a todos los lectores</h2>
De esta manera, el título «Hola a todos los lectores» se mostrará en negrita.
Ejemplo 2: Lista con elementos importantes
Si tienes una lista de elementos y quieres resaltar los más importantes, puedes utilizar la etiqueta <strong> para destacarlos:
<ul> <li>El primer elemento</li> <li>El segundo elemento es muy importante</li> <li>El tercer elemento</li> </ul>
En este caso, el segundo elemento de la lista se mostrará en negrita.
Ejemplo 3: Texto en negrita
Si simplemente quieres resaltar una parte del texto, sin utilizar encabezados o listas, puedes utilizar la etiqueta <b> para poner ese texto en negrita:
<p>Este es un texto en negrita.</p>
De esta forma, la frase «texto en negrita» se mostrará en negrita dentro del párrafo.
Estos son solo algunos ejemplos de cómo utilizar etiquetas HTML como <strong> y <b> para resaltar frases importantes o destacar contenido en tu página web. Recuerda que estas etiquetas son solo algunas de las muchas opciones que tienes disponibles para dar formato a tus textos.
Casos especiales
En ciertos casos, hay frases dentro del texto que son especialmente importantes y necesitan resaltarse. Para lograr esto, podemos utilizar diferentes etiquetas HTML para resaltar el contenido de manera visual y semántica.
Etiqueta
La etiqueta es utilizada para resaltar texto de manera enfática. Al usar esta etiqueta, el texto contenido dentro de ella se mostrará en negrita en el navegador.
Un ejemplo de uso de la etiqueta es el siguiente: «El futuro es incierto, pero con dedicación podemos lograr nuestros objetivos». En este caso, la palabra «futuro» se muestra en negrita para resaltar su importancia en la frase.
Etiqueta
La etiqueta también se utiliza para resaltar texto en negrita. Sin embargo, a diferencia de la etiqueta , la etiqueta no añade significado semántico al texto.
Por ejemplo: «Necesito urgentemente una respuesta». Aquí, la palabra «urgentemente» se muestra en negrita utilizando la etiqueta para destacarla en la frase.
Listas en HTML
Las listas son utilizadas para agrupar elementos relacionados. Las listas pueden ser ordenadas (
- ) o no-ordenadas (
- ). Dentro de estas listas, también podemos aplicar formatos para resaltar algunas frases.
Por ejemplo, podriamos tener una lista de tareas con frases resaltadas utilizando la etiqueta o :
- Lavar los platos
- Ir al supermercado
- Recoger la ropa
- Pagar las facturas
En esta lista, la tarea «Recoger la ropa» se muestra resaltada utilizando la etiqueta .
En conclusión, cuando nos encontramos con casos especiales en los que necesitamos resaltar frases importantes en nuestros textos, disponemos de varias opciones. Podemos utilizar las etiquetas o para aplicar formato de negrita, e incluso aprovechar las listas en HTML para resaltar el contenido relevante.