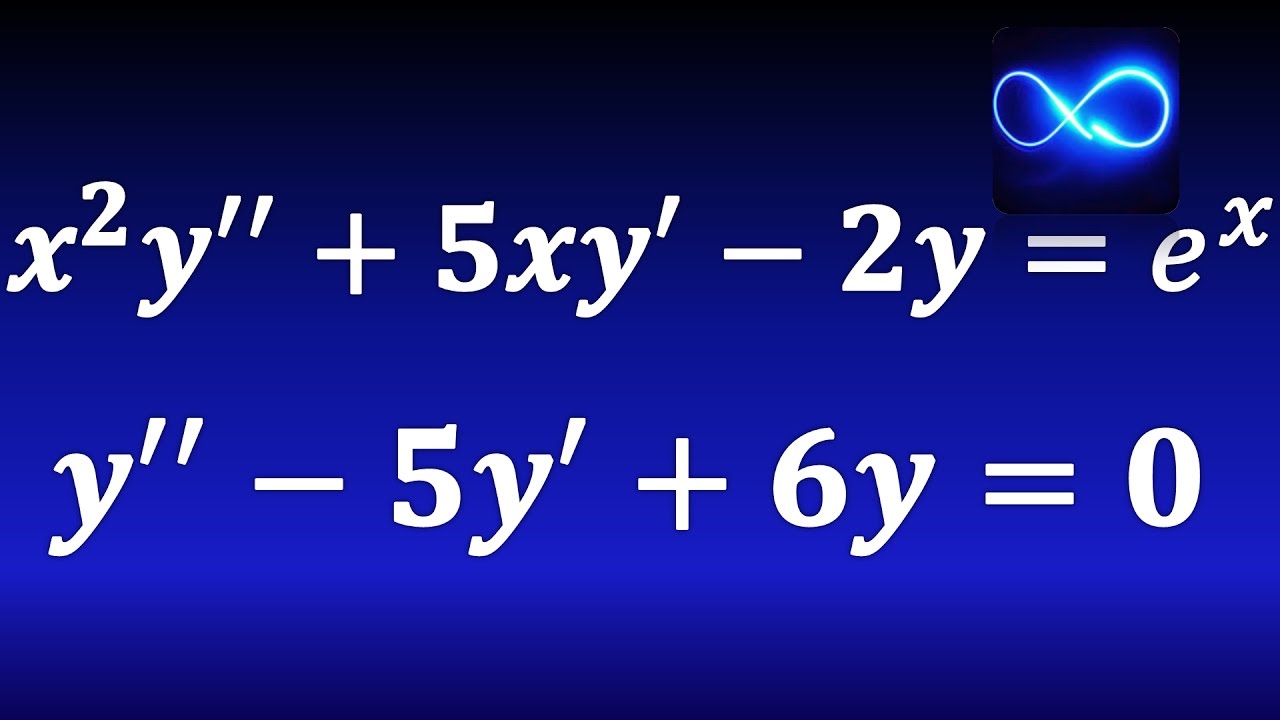Ecuación diferencial de segundo orden con función seno y coeficiente lineal

Ecuaciones diferenciales de segundo orden

Las ecuaciones diferenciales de segundo orden son un tipo de ecuaciones que involucran una función desconocida y sus derivadas hasta segundo orden. Estas ecuaciones son ampliamente utilizadas en diversas áreas de la física y la ingeniería.

Una ecuación diferencial de segundo orden se puede representar de la siguiente manera:

d²y/dx² + P(x)dy/dx + Q(x)y = R(x)

Donde y = y(x) representa la función desconocida, P(x), Q(x) y R(x) son funciones conocidas y x es la variable independiente.

Tipos de ecuaciones diferenciales de segundo orden

Existen diferentes tipos de ecuaciones diferenciales de segundo orden, entre los más comunes se encuentran:

• Las ecuaciones diferenciales lineales homogéneas, que se caracterizan por tener P(x) = Q(x) = R(x) = 0.
• Las ecuaciones diferenciales lineales no homogéneas, que se caracterizan por tener P(x), Q(x) y/o R(x) diferentes de cero.
• Las ecuaciones diferenciales no lineales, que pueden involucrar términos no lineales de la función desconocida y/o sus derivadas.

Para resolver una ecuación diferencial de segundo orden, es necesario encontrar una solución particular que satisfaga la ecuación. Esto se puede lograr mediante diferentes métodos, como por ejemplo el método de coeficientes indeterminados, el método de variación de parámetros o el método de coeficientes constantes.

En conclusión, las ecuaciones diferenciales de segundo orden son una herramienta fundamental en el estudio de fenómenos físicos y naturales, y su resolución puede brindar información valiosa para comprender el comportamiento de diversos sistemas.

Funciones seno en ecuaciones diferenciales de segundo orden

Introducción:

Las funciones seno desempeñan un papel crucial en el estudio de las ecuaciones diferenciales de segundo orden. Estas ecuaciones son de gran interés en matemáticas y física debido a su amplia variedad de aplicaciones. En este artículo exploraremos cómo las funciones seno pueden ser utilizadas en la resolución de este tipo de ecuaciones.

Ecuaciones diferenciales de segundo orden:

Una ecuación diferencial de segundo orden es una ecuación que relaciona una función desconocida y sus derivadas de segundo orden. Generalmente, estas ecuaciones se expresan de la forma:

Texto explicativo:

1. Forma general: y” + p(x)y’ + q(x)y = f(x)
2. Función seno como solución: Cuando la función f(x) en la ecuación anterior es igual a cero, es posible encontrar soluciones mediante la función seno. Si consideramos la solución y(x) = A sin(wx), donde A y w son constantes, podemos sustituir en la ecuación y sus derivadas y encontrar el valor de p(x) y q(x) que lo hacen una solución válida.
3. Valores límite: Es importante tener en cuenta que la función seno es una solución para valores límite específicos. El valor de w está determinado por las condiciones iniciales o de contorno del problema en cuestión.
4. Aplicaciones: Las ecuaciones diferenciales de segundo orden con funciones seno como solución encuentran aplicaciones en diversos campos, como la mecánica, la física de ondas y la teoría de circuitos.

Conclusiones:

En resumen, las funciones seno desempeñan un papel fundamental en la resolución de ecuaciones diferenciales de segundo orden. Esto se debe a sus propiedades características y su amplia aplicabilidad en diferentes campos de la ciencia y la ingeniería. La capacidad de utilizar funciones seno como solución proporciona herramientas poderosas para resolver problemas complejos en estos ámbitos.

Coeficiente lineal en ecuaciones diferenciales de segundo orden

En las ecuaciones diferenciales de segundo orden, el coeficiente lineal es uno de los elementos clave que determina el comportamiento de la solución.

En una ecuación diferencial de segundo orden, la forma general es:
a(x)y” + b(x)y’ + c(x)y = f(x)

Donde:
– a(x) es el coeficiente principal, que multiplica la segunda derivada de la función y(x).
– b(x) es el coeficiente lineal, que multiplica la primera derivada de la función y(x).
– c(x) es el coeficiente constante, que multiplica la función y(x).
– f(x) es una función conocida.

El coeficiente lineal b(x) es lo que determina la proporcionalidad entre la tasa de cambio de y(x) y la función en sí misma. Si b(x) es positivo, significa que la función y(x) tiene una tendencia a aumentar a medida que x aumenta. Por otro lado, si b(x) es negativo, la función y(x) tendrá una tendencia a disminuir a medida que x aumenta.

Es importante tener en cuenta que el coeficiente lineal b(x) también puede estar presente en términos no lineales. En este caso, la interpretación del coeficiente lineal puede variar dependiendo de la naturaleza de la ecuación diferencial.

En resumen, el coeficiente lineal en ecuaciones diferenciales de segundo orden es fundamental para comprender el comportamiento y la dirección de la solución de la ecuación. Su signo determina si la función y(x) tiende a aumentar o disminuir a medida que x aumenta.

Resolviendo la ecuación diferencial de segundo orden con función seno y coeficiente lineal

En matemáticas, una ecuación diferencial de segundo orden es una ecuación que involucra una función desconocida y sus derivadas de segundo orden. Resolver este tipo de ecuaciones puede ser un desafío, pero al aplicar los métodos adecuados, es posible llegar a una solución.

En este artículo, nos vamos a enfocar en la resolución de una ecuación diferencial de segundo orden que involucra una función seno y un coeficiente lineal. La ecuación tiene la siguiente forma:

d²y/dx² + a*(dy/dx) + b*sin(x) = 0

Paso 1: Identificar los coeficientes

Lo primero que debemos hacer es identificar los coeficientes en la ecuación diferencial. En este caso, tenemos el coeficiente lineal a y el coeficiente de la función seno b.

Paso 2: Resolver la ecuación homogénea asociada

El siguiente paso es resolver la ecuación homogénea asociada, que se obtiene al igualar la ecuación diferencial a cero. Esto nos dará las soluciones de la forma y_h(x) = C₁*f₁(x) + C₂*f₂(x), donde C₁ y C₂ son constantes y f₁(x) y f₂(x) son funciones linealmente independientes.

En nuestro caso, la ecuación homogénea asociada es:

d²y/dx² + a*(dy/dx) + b*sin(x) = 0

Paso 3: Encontrar una solución particular

Una vez que hemos resuelto la ecuación homogénea asociada, debemos encontrar una solución particular de la ecuación diferencial. Esta solución tendrá la forma general y_p(x).

En este caso, podemos suponer que y_p(x) = A*cos(x) + B*sin(x) es una solución particular, donde A y B son constantes.

Sustituyendo esta solución en la ecuación diferencial, obtendremos los valores de A y B.

Paso 4: Sumar la solución general

Una vez que hemos encontrado la solución particular, podemos sumarla a la solución homogénea para obtener la solución general de la ecuación diferencial de segundo orden.

La solución general será de la forma y(x) = y_h(x) + y_p(x), donde y_h(x) es la solución homogénea y y_p(x) es la solución particular.

En resumen, resolver una ecuación diferencial de segundo orden con función seno y coeficiente lineal puede involucrar varios pasos, como identificar los coeficientes, resolver la ecuación homogénea asociada, encontrar una solución particular y sumarla a la solución homogénea para obtener la solución general. Con el conocimiento adecuado y la aplicación de los métodos correctos, es posible resolver este tipo de ecuaciones de manera efectiva.

Ejemplos prácticos de ecuaciones diferenciales de segundo orden con función seno y coeficiente lineal

Las ecuaciones diferenciales son herramientas fundamentales en el estudio de fenómenos naturales y científicos. En particular, las ecuaciones diferenciales de segundo orden son aquellas en las que aparecen derivadas de segundo orden. Estas ecuaciones se pueden encontrar en muchas áreas de la física y la ingeniería, y se caracterizan por tener una función seno y un coeficiente lineal.

Ejemplo 1:

Consideremos la siguiente ecuación diferencial de segundo orden:

y” + 2y’ + y = sin(x)

Donde y representa una función desconocida, y’ es la derivada de y con respecto a x, y” es la derivada segunda de y con respecto a x, y sin(x) es una función seno.

Esta ecuación es lineal, ya que no hay productos o potencias de y o sus derivadas. Además, el coeficiente lineal es 2. Podemos utilizar técnicas como la transformada de Laplace o el método de variación de parámetros para encontrar la solución de esta ecuación diferencial.

Ejemplo 2:

Ahora consideremos otra ecuación diferencial de segundo orden:

y” + 3y’ + 2y = sen(2x)

En este caso, la función seno tiene un coeficiente delante de ella (2x en lugar de x). Esto indica que la función seno se repite con una frecuencia doble en comparación con el ejemplo anterior. Al igual que en el primer ejemplo, podemos aplicar diferentes métodos para resolver esta ecuación diferencial.

Estos son solo dos ejemplos prácticos de ecuaciones diferenciales de segundo orden con función seno y coeficiente lineal. Existen múltiples aplicaciones en la física y la ingeniería donde estas ecuaciones son de gran importancia y requieren técnicas especializadas para su resolución.