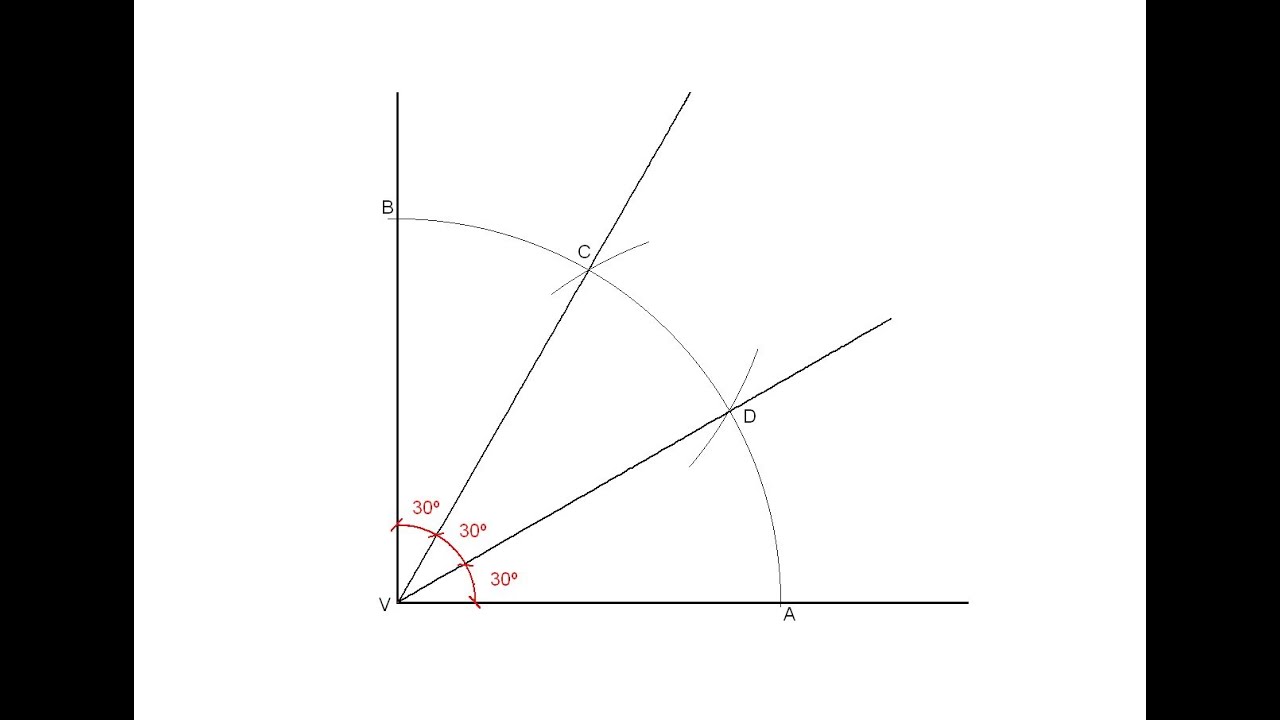
¿Qué significa dividir un ángulo interior en dos ángulos iguales mediante una recta?
Dividir un ángulo interior en dos ángulos iguales mediante una recta significa trazar una línea recta desde un punto dentro del ángulo hasta uno de sus lados, de modo que los dos ángulos resultantes tengan la misma medida.
Esta técnica se conoce como «bisectar» el ángulo interior, y se utiliza en geometría para obtener dos ángulos iguales que comparten un mismo vértice.
La bisectriz de un ángulo divide al ángulo en dos partes iguales, creando dos ángulos que tienen la misma medida y que suman la medida original del ángulo.
La bisectriz también se utiliza en la resolución de problemas geométricos y en la construcción de figuras simétricas.
En resumen, dividir un ángulo interior en dos ángulos iguales mediante una recta significa obtener dos ángulos con la misma medida a partir de un ángulo original, utilizando una línea recta llamada bisectriz. Esta técnica es fundamental en geometría y tiene diversas aplicaciones en problemas y construcciones geométricas.
¿Por qué es importante dividir un ángulo interior en dos ángulos iguales mediante una recta?
La división de un ángulo interior en dos ángulos iguales mediante una recta es un concepto importante en geometría. Esto se conoce como la bisectriz del ángulo y tiene varias aplicaciones y beneficios.
Propiedad de los ángulos iguales
Dividir un ángulo interior en dos ángulos iguales es útil porque permite hacer afirmaciones y trabajar con propiedades geométricas relacionadas con los ángulos. Cuando una recta bisecta un ángulo, los dos ángulos resultantes son siempre iguales, independientemente del tamaño del ángulo original. Esto facilita la resolución de problemas geométricos y la demostración de teoremas.
Construcción de triángulos
La división de un ángulo interior en dos ángulos iguales mediante una recta también es importante en la construcción de triángulos. Al bisectar uno de los ángulos del triángulo, es posible encontrar el punto medio de uno de los lados y construir un triángulo equilátero o isósceles, que puede ser necesario en determinadas situaciones o diseños.
La construcción de triángulos es una habilidad esencial en geometría y es utilizada en distintas aplicaciones prácticas, como la arquitectura, la ingeniería y la cartografía.
Resolución de problemas de simetría
La bisectriz de un ángulo es también relevante en la resolución de problemas relacionados con la simetría. Si se quiere encontrar el punto de simetría en relación a una figura, es necesario encontrar la bisectriz de un ángulo dado para asegurarse de que los puntos están equidistantes de la línea.
Relación con otros conceptos geométricos
La división de un ángulo en dos ángulos iguales mediante una recta también está relacionada con otros conceptos geométricos, como las líneas paralelas y perpendiculares, así como la suma de ángulos y las relaciones trigonométricas. Comprender cómo dividir un ángulo y trabajar con ángulos iguales es fundamental para el estudio y la aplicación de la geometría en diferentes campos.
En conclusión, la división de un ángulo interior en dos ángulos iguales mediante una recta es importante debido a las propiedades y aplicaciones geométricas que implica. Esta habilidad facilita la resolución de problemas, la construcción de triángulos, la comprensión de la simetría y la relación con otros conceptos geométricos. Es una herramienta fundamental para desarrollar un pensamiento geométrico sólido.
¿Cuál es el método para dividir un ángulo interior en dos ángulos iguales mediante una recta?
Para dividir un ángulo interior en dos ángulos iguales mediante una recta, se utiliza el método de la bisectriz.
La bisectriz de un ángulo es la recta que divide el ángulo en dos ángulos iguales.
El procedimiento para trazar la bisectriz de un ángulo es el siguiente:
- Dibujar el ángulo dado con los puntos de origen y extremo claramente marcados.
- Tomar un compás y trazar un arco desde el vértice del ángulo.
- Marcar dos puntos en el arco, a una distancia razonablemente constante del vértice.
- Desde cada uno de los puntos marcados en el arco, trazar otro arco que corte al primer arco en un par de puntos diferentes.
- Unir los puntos de intersección del segundo arco con la recta que define el ángulo.
- La recta trazada a través del vértice del ángulo y los puntos de intersección es la bisectriz del ángulo, dividiéndolo en dos ángulos iguales.
Este método se aplica tanto para ángulos agudos como para ángulos obtusos.
¡Recuerda siempre marcar bien los pasos y tener paciencia al trazar las bisectrices!
Ejemplo práctico de división de un ángulo
En matemáticas, la división de un ángulo es una operación que consiste en dividir un ángulo dado en partes iguales. Esto puede ser útil para calcular medidas o para trazar líneas paralelas en construcciones geométricas.
Para ilustrar este concepto, vamos a tomar un ángulo de 360 grados y dividirlo en 6 partes iguales. Para hacer esto, primero debemos determinar cuántos grados representa cada una de las partes.
Usando la fórmula para dividir un ángulo, donde el ángulo original se divide entre el número de partes que deseamos obtener, podemos calcular que cada una de las partes del ángulo será de 60 grados.
Ahora, vamos a trazar las divisiones del ángulo en un círculo. Para esto, podemos utilizar una brújula y un transportador. Marcamos el centro del círculo y trazamos un arco con la brújula. Luego, utilizando el transportador, hacemos marcas cada 60 grados alrededor del círculo.
Una vez que tengamos las divisiones marcadas en el círculo, podemos utilizar estas divisiones para trazar líneas paralelas o realizar cálculos geométricos utilizando los ángulos creados.
En resumen, la división de un ángulo consiste en dividir un ángulo dado en partes iguales. Para hacer esto, podemos utilizar la fórmula de división de ángulos y trazar las divisiones en un círculo utilizando una brújula y un transportador. Esto puede ser útil en muchas aplicaciones matemáticas y geométricas.
En este artículo, hemos explorado varios temas relacionados con HTML y su uso en la creación de blogs. A través de ejemplos y ejercicios prácticos, hemos aprendido sobre etiquetas y su función en la estructura y apariencia de un sitio web.
Es importante destacar la importancia del uso de etiquetas HTML adecuadas para garantizar la accesibilidad y la legibilidad del contenido. El uso de etiquetas como <h1>, <p> y <a> nos permite organizar y enlazar nuestro contenido de manera eficiente.
También hemos discutido la importancia de la semántica en HTML. El uso de etiquetas semánticas como <header>, <nav> y <article> nos ayuda a estructurar y dar sentido al contenido, mejorando así la experiencia de usuario.
Otro punto importante a considerar es la inclusión de elementos multimedia en nuestro blog. Con el uso de etiquetas como <img> y <video>, podemos agregar imágenes y videos que complementen nuestro contenido y lo hagan más atractivo y dinámico para los lectores.
En conclusión, HTML es un lenguaje fundamental en la creación de páginas web y blogs. Con un conocimiento básico de sus etiquetas y su aplicación, podemos crear contenido accesible, semánticamente correcto y atractivo para nuestros lectores.