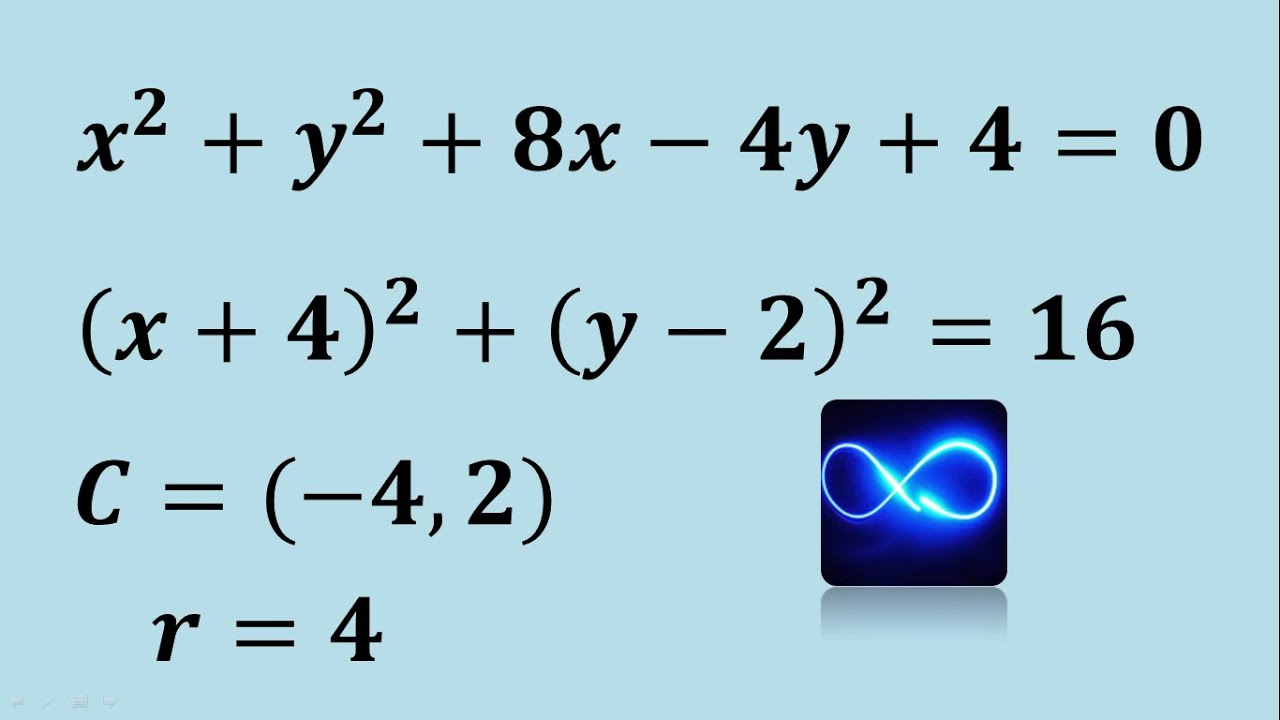Ecuación general de una circunferencia: x2+y2−2x+4y−4=0

¿Qué es la ecuación general de una circunferencia?

La ecuación general de una circunferencia es una forma matemática de describir una circunferencia en un plano cartesiano.

La ecuación general de una circunferencia se puede expresar de la siguiente manera:

x^2 + y^2 + Ax + By + C = 0

Donde x e y son las coordenadas de un punto en el plano cartesiano, A, B y C son constantes que determinan la posición y tamaño de la circunferencia.

Esta ecuación general nos permite determinar la ubicación y características de una circunferencia en el plano cartesiano. Al manipular los valores de A, B y C, podemos trasladar, escalar o rotar la circunferencia.

La ecuación general de una circunferencia también puede ser expresada en una forma más simple, conocida como la ecuación ordinaria de una circunferencia:

(x – h)^2 + (y – k)^2 = r^2

Donde (h, k) es el centro de la circunferencia y r es el radio.

En resumen, la ecuación general de una circunferencia es una forma matemática que nos permite describir la posición y tamaño de una circunferencia en el plano cartesiano.

Desglose de la ecuación general de la circunferencia

La ecuación general de la circunferencia se representa de la siguiente manera:

H² + K² + 2Gx + 2Fy + C = 0

Donde:

• H es el coeficiente de x²;
• K es el coeficiente de y²;
• G es el coeficiente de x;
• F es el coeficiente de y;
• C es el término independiente.

Esta ecuación general se utiliza para representar cualquier circunferencia en el plano cartesiano. Cada uno de los coeficientes y el término independiente determinan las características de la circunferencia.

Por ejemplo, cuando los coeficientes H y K son iguales, la circunferencia está centrada en el origen del plano. Si los coeficientes G y F son diferentes de cero, la circunferencia estará desplazada en el plano en dirección horizontal (G) y vertical (F).

La ecuación general de la circunferencia es una forma más generalizada de la ecuación de la circunferencia que se puede expresar en la forma:

(x – a)² + (y – b)² = r²

Donde (a, b) representa el centro de la circunferencia y r es el radio.

Es importante entender el desglose de la ecuación general de la circunferencia para poder analizar y graficar circunferencias con diferentes características en el plano cartesiano.

Cómo encontrar el centro y el radio de la circunferencia

En geometría, una circunferencia es una figura plana que está compuesta por todos los puntos que se encuentran a la misma distancia de un punto central llamado centro. Además, la circunferencia también está definida por un único valor llamado radio, que es la distancia entre el centro y cualquier punto de la circunferencia.

Para encontrar el centro y el radio de una circunferencia, se pueden seguir los siguientes pasos:

1. Determinar al menos tres puntos distintos en la circunferencia. Estos puntos pueden ser proporcionados en el problema o se pueden encontrar a partir de información adicional.
2. Construir las rectas perpendiculares a los segmentos que unen los puntos elegidos con su punto medio. Estas rectas se cruzarán en un punto, que será el centro de la circunferencia.
3. Medir la distancia entre el centro y uno de los puntos de la circunferencia para obtener el radio de la circunferencia.

Es importante recordar que estos pasos solo son aplicables si se conocen al menos tres puntos distintos en la circunferencia. En caso de tener menos información, se necesitaría de otros métodos o cálculos adicionales para encontrar el centro y el radio de la circunferencia.

En resumen, el centro y el radio de una circunferencia se pueden encontrar a través de la determinación de al menos tres puntos en la circunferencia y la construcción de rectas perpendiculares a los segmentos que unen estos puntos con su punto medio.

Ejemplo de resolución de una ecuación de circunferencia

Ecuaciones de la forma (x – h)^2 + (y – k)^2 = r^2 representan circunferencias en un plano cartesiano, donde (h, k) es el centro de la circunferencia y r es el radio.

Para resolver una ecuación de la circunferencia, debemos seguir los siguientes pasos:

1. Identificar los valores de h, k y r. En la ecuación (x – h)^2 + (y – k)^2 = r^2, h y k corresponden a las coordenadas del centro de la circunferencia, y r es el radio.
2. Dibujar la circunferencia. Usando un sistema de coordenadas, marcamos el punto (h, k) como el centro y trazamos la circunferencia con un radio de longitud r.
3. Resolver puntos en la circunferencia. Para encontrar puntos en la circunferencia, podemos elegir valores para x (o y) y luego sustituirlos en la ecuación original. Resolveremos la ecuación para obtener el valor de y (o x) correspondiente al punto en la circunferencia.

Por ejemplo, consideremos la ecuación (x – 2)^2 + (y + 3)^2 = 25. En este caso, el centro de la circunferencia es (2, -3) y el radio es √25 = 5.

Podemos dibujar la circunferencia en un plano cartesiano, marcando el punto (2, -3) como el centro y trazando la circunferencia con un radio de longitud 5.

Para encontrar algunos puntos en la circunferencia, seleccionemos un valor para x. Supongamos x = 0.

Sustituyendo en la ecuación original, obtenemos (0 – 2)^2 + (y + 3)^2 = 25. Simplificando, tenemos 4 + (y + 3)^2 = 25.

Resolviendo para y, tenemos (y + 3)^2 = 21. Tomando la raíz cuadrada en ambos lados, obtenemos y + 3 = ±√21. Despejando y, obtenemos y = -3 ±√21.

Por lo tanto, los puntos correspondientes en la circunferencia para x = 0 son (0, -3 + √21) y (0, -3 – √21).

Repetimos este proceso para otros valores de x para obtener más puntos en la circunferencia.

En resumen, para resolver una ecuación de la circunferencia, identificamos los valores de h, k y r, dibujamos la circunferencia en un plano cartesiano y encontramos puntos en la circunferencia sustituyendo valores para x (o y) en la ecuación original.

Propiedades y características de una circunferencia

Una circunferencia es una figura geométrica formada por todos los puntos equidistantes de un punto fijo llamado centro. A continuación, se presentan algunas de las propiedades y características importantes de una circunferencia:

– Diámetro: El diámetro de una circunferencia es la distancia más larga que se puede trazar entre dos puntos en la circunferencia. El diámetro siempre pasa por el centro de la circunferencia.

– Radio: El radio de una circunferencia es la distancia desde el centro de la circunferencia hasta un punto cualquiera en la circunferencia. Todos los radios de una circunferencia tienen la misma longitud.

– Cuerda: Una cuerda es un segmento de línea recta que une dos puntos en la circunferencia. Una cuerda puede pasar por el centro de la circunferencia (diámetro) o puede ser cualquier otro segmento de línea recta.

– Tangente: Una tangente es una línea recta que toca la circunferencia en un solo punto, sin cruzarla. La tangente es perpendicular al radio trazado hasta el punto de contacto.

– Arco: Un arco es una porción de la circunferencia. La longitud de un arco se mide en unidades como grados, radianes o unidades de longitud.

– Circunferencia unitaria: Una circunferencia unitaria es una circunferencia cuyo radio tiene una longitud de uno.

– Ángulo central: Un ángulo central es aquel que tiene su vértice en el centro de la circunferencia y sus lados son dos radios o cuerdas.

– Ángulo inscrito: Un ángulo inscrito es aquel que tiene su vértice en la circunferencia y sus lados son cordones que intersectan la circunferencia.

Estas son solo algunas de las propiedades y características de una circunferencia. Esta figura geométrica es de gran importancia y se utiliza en muchas ramas de las matemáticas y ciencias aplicadas.