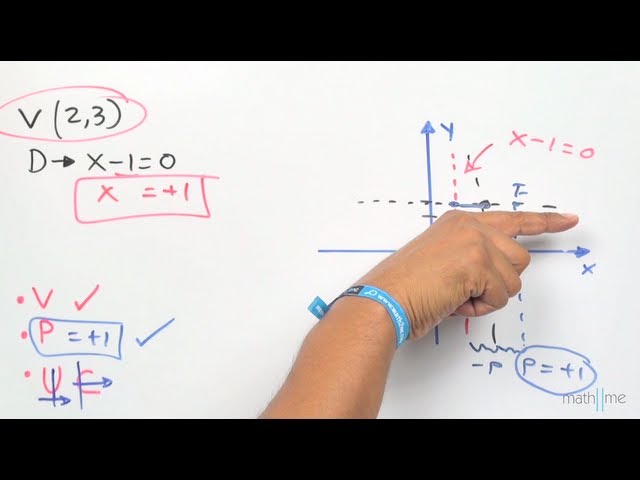La parábola es una de las curvas cónicas más importantes en matemáticas, y su ecuación fundamental es conocida por todos los estudiantes de álgebra. La característica más distintiva de una parábola es la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz. Esta propiedad especial define muchas de las propiedades y comportamientos únicos de las parábolas y es crucial para comprender su naturaleza y aplicaciones en campos como la física, la ingeniería y la óptica.
La Definición Fundamental de la Parábola
La definición fundamental de una parábola establece que para cada punto P en la curva, la distancia entre P y el foco (F) es igual a la distancia entre P y la directriz. Este concepto es la base para comprender la forma y la simetría de la parábola, así como su construcción geométrica. Ahondemos más en los detalles y las implicaciones de esta igualdad de distancias.
Forma Canónica de la Ecuación de la Parábola
La forma canónica de la ecuación de la parábola es y = ax^2 + bx + c (o x = ay^2 + by + c si la parábola está orientada horizontalmente). En esta forma, el punto (h, k) representa el vértice de la parábola. La distancia entre el vértice y el foco, así como entre el vértice y la directriz, desencadena las propiedades matemáticas inherentes a la parábola que la hacen tan intrigante.
La Igualdad de Distancias y la Simetría de la Parábola
La igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es el fundamento de la simetría de una parábola. Esta simetría se manifiesta en la reflectividad de la luz y el sonido, así como en la trayectoria de los objetos en movimiento que siguen una trayectoria parabólica. La comprensión de esta simetría es crucial para el diseño de sistemas ópticos y para predecir el comportamiento de los fenómenos naturales y artificiales que siguen un patrón parabólico.
La Intersección entre la Parábola y la Línea Directriz
Una exploración detallada de la intersección entre la parábola y la línea directriz revela una relación fundamental con la distancia entre el foco y el vértice. Esta relación es esencial para trazar y analizar la forma de la parábola, así como para interpretar sus propiedades geométricas y algebraicas.
Las Aplicaciones Prácticas de la Igualdad de Distancias en Ingeniería
En ingeniería, la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es de suma importancia para el diseño de antenas parabólicas, espejos cóncavos para sistemas ópticos, y reflectores parabólicos para concentrar y dirigir la luz y las ondas electromagnéticas. También es fundamental para la planificación y el análisis de trayectorias de proyectiles y vehículos en movimiento.
El Comportamiento de la Luz y el Sonido en una Parábola
La igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es esencial para entender cómo la luz y el sonido se reflejan y se enfocan en un sistema parabólico. Esta propiedad es explotada en telescopios, reflectores de micrófonos, y reflectores en escenarios para dirigir el sonido hacia la audiencia. La precisión y eficiencia de estos sistemas dependen de la igualdad de distancias en su diseño y construcción.
La Importancia de la Igualdad de Distancias en Óptica
En la óptica, la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es esencial para el diseño de lentes y espejos que generan imágenes nítidas y sin distorsiones. Este concepto define las características de enfoque y dispersión de los sistemas ópticos, y es crucial en la fabricación de lentes oftálmicas, microscopios, y otros dispositivos ópticos de uso diario.
La Igualdad de Distancias en la Naturaleza
La igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz se observa en muchos fenómenos naturales, desde la trayectoria de una gota de agua al caer hasta la forma de asteroides y cometas en movimiento. La parábola es un modelo matemático preciso para describir estos fenómenos, y esta igualdad de distancias es el motivo subyacente de su comportamiento.
La Igualdad de Distancias y las Ecuaciones de Movimiento
En la física, la igualdad de distancias es fundamental para modelar y predecir las ecuaciones de movimiento de objetos en caída libre, proyectiles, y cuerpos celestes en órbita. Estas aplicaciones demuestran cómo la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es crucial para entender y predecir los movimientos en el espacio y en la tierra.
La Igualdad de Distancias y la Teoría de las Ecuaciones Cuadráticas
La igualdad de distancias en la parábola es un tema central en la teoría de las ecuaciones cuadráticas. Este concepto es fundamental para resolver problemas algebraicos y geométricos, y es una base para muchos otros conceptos matemáticos avanzados. Además, la aplicación de esta igualdad de distancias en contextos de ingeniería, física y óptica demuestra su profunda importancia en la resolución de problemas prácticos y teóricos.
La Igualdad de Distancias y la Forma Estándar de la Ecuación de la Parábola
La forma estándar de la ecuación de la parábola, (x-h)^2 = 4p(y-k), es una representación directa de la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz. Esta forma revela la influencia directa de esta igualdad en la disposición y la forma de la parábola, y muestra cómo los parámetros pueden ajustarse para lograr diferentes configuraciones geométricas y ópticas.
La Igualdad de Distancias y el Teorema de la Reflexión
El teorema de la reflexión establece que un rayo de luz emitido por el foco de una parábola se reflejará en su superficie y viajará en dirección a la línea directriz. Esta propiedad es una consecuencia directa de la igualdad de distancias y es esencial en la óptica geométrica y la ingeniería óptica. La predicción y control preciso de estas reflexiones son cruciales en aplicaciones que van desde la iluminación arquitectónica hasta la fabricación de lentes y reflectores de precisión.
La Igualdad de Distancias en el Diseño de Sistemas Acústicos
En el diseño de sistemas de sonido, la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es crucial para la producción de un sonido enfocado y direccional. Desde altavoces hasta sistemas de megafonía, la comprensión de esta igualdad se traduce en un diseño efectivo y una experiencia auditiva de alta calidad para el público.
La Igualdad de Distancias en la Teoría de Lentes y Espejos
La igualdad de distancias es un principio fundamental en la teoría de lentes y espejos. Esta idea se aplica en la formación de imágenes en sistemas ópticos y en la corrección de aberraciones ópticas para obtener imágenes nítidas y precisas. La igualdad de distancias es crucial en el diseño y la fabricación de lentes para gafas, cámaras, microscopios y otros dispositivos ópticos de uso diario.
El Papel de la Igualdad de Distancias en Astronomía
En astronomía, la igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es esencial para modelar y predecir las órbitas de objetos celestes, desde asteroides y cometas hasta satélites y planetas. Esta propiedad geométrica subyacente es crucial para entender y predecir los movimientos de los cuerpos celestes en el espacio.
Conclusión
La igualdad de distancias entre el foco y el vértice y entre el vértice y la directriz es un concepto fundamental que define muchas propiedades matemáticas, geométricas y físicas de la parábola. Esta igualdad es crucial en campos tan diversos como la ingeniería, la óptica, la física y las matemáticas aplicadas, y su comprensión es esencial para diseñar, analizar y aplicar sistemas parabólicos en la vida cotidiana y en la exploración del universo. La exploración de esta igualdad de distancias revela la riqueza y la profundidad de su importancia en nuestra comprensión del mundo que nos rodea y en la resolución de problemas prácticos y teóricos.