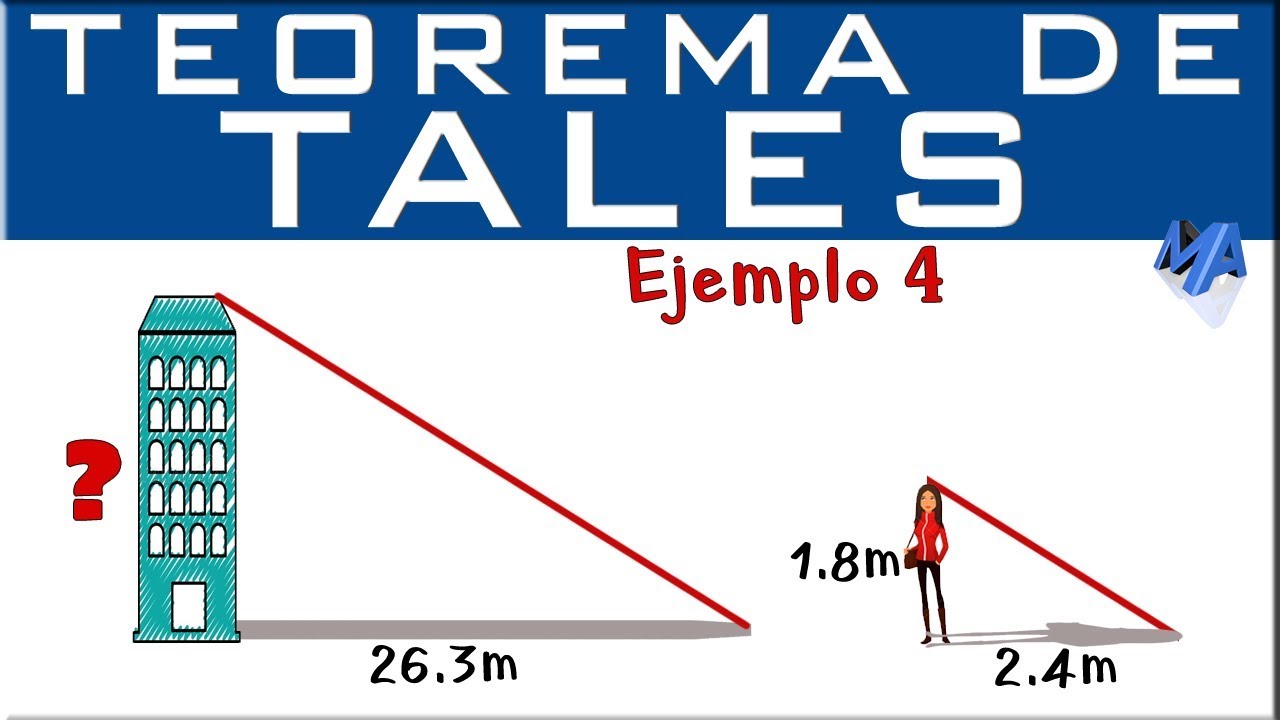
Calcular la altura de un árbol puede parecer una tarea desafiante, pero con la aplicación adecuada de conceptos matemáticos, podemos simplificar el proceso utilizando la similitud de triángulos.
Al comprender la teoría detrás de este enfoque y seguir un conjunto de pasos específicos, podrás determinar la altura de un árbol con relativa facilidad. A continuación, exploraremos detalladamente este proceso.
Conceptos clave
Para comenzar, es fundamental entender los conceptos clave que subyacen a este método de cálculo. La similitud de triángulos es un principio fundamental en geometría que establece que dos triángulos son similares si tienen todos sus ángulos correspondientes iguales y sus lados son proporcionales. Esta idea es esencial para el cálculo de alturas que se encuentran fuera de nuestro alcance físico directo.
Identificación de los elementos
La primera etapa de este proceso implica la identificación de los elementos necesarios. Necesitarás un objeto de longitud conocida, como un palo o una regla, y su sombra proyectada en el suelo. Adicionalmente, deberás medir la sombra proyectada por el árbol en el mismo momento en que mides la sombra del objeto de longitud conocida.
Cálculo de la altura
Con los datos recolectados, el cálculo de la altura del árbol implica el uso de la proporción entre las sombras proyectadas y las respectivas alturas de los objetos. Este proceso requiere atención a los detalles y la aplicación precisa de las fórmulas matemáticas pertinentes.
Pasos detallados
Paso 1: Medir la sombra del objeto de longitud conocida
Encuentra un momento durante el día en que el sol esté proyectando sombras claramente definidas. Coloca el objeto de longitud conocida, como el palo o la regla, verticalmente en el suelo y mide su sombra con una cinta métrica o un instrumento similar. Registra esta medida.
Paso 2: Medir la sombra del árbol
En el mismo momento en que mediste la sombra del objeto de longitud conocida, mide la sombra proyectada por el árbol utilizando el mismo procedimiento que en el paso anterior. Asegúrate de anotar esta medida con precisión.
Paso 3: Medición de la altura del objeto de longitud conocida
Utilizando una cinta métrica o instrumento similar, mide la altura real del objeto de longitud conocida (palo, regla, etc.). Esta medida se utilizará en la siguiente fase de cálculos.
Paso 4: Aplicación de la similitud de triángulos
Utilizando los datos recopilados en los pasos anteriores, aplica el concepto de similitud de triángulos para establecer una proporción entre las sombras proyectadas y las alturas reales tanto del objeto conocido como del árbol. Este paso es crucial para el cálculo preciso de la altura del árbol.
Paso 5: Cálculo final
Finalmente, utilizando la proporción obtenida en el paso anterior, procede a calcular la altura del árbol. Este cálculo puede realizarse de forma manual o mediante el uso de una calculadora, asegurándote de emplear las cifras correctas para obtener un resultado preciso.
Consideraciones importantes
Precisión en las mediciones
Es crucial asegurarse de realizar todas las mediciones con la máxima precisión posible. La exactitud de los datos recolectados tendrá un impacto directo en la precisión del cálculo final.
Condiciones de iluminación
Ten en cuenta que las condiciones de iluminación pueden afectar la longitud de las sombras proyectadas. Procura realizar las mediciones en un momento del día en el que las sombras sean claramente definidas y consistentes.
Calcular la altura de un árbol utilizando la similitud de triángulos puede ser un proceso desafiante pero gratificante. Al comprender y aplicar los conceptos matemáticos involucrados, podrás obtener una estimación precisa de la altura de un árbol sin la necesidad de escaleras u otros equipos complicados. Recuerda la importancia de la precisión en las mediciones y ajustes adecuados para las condiciones ambientales al realizar este cálculo.