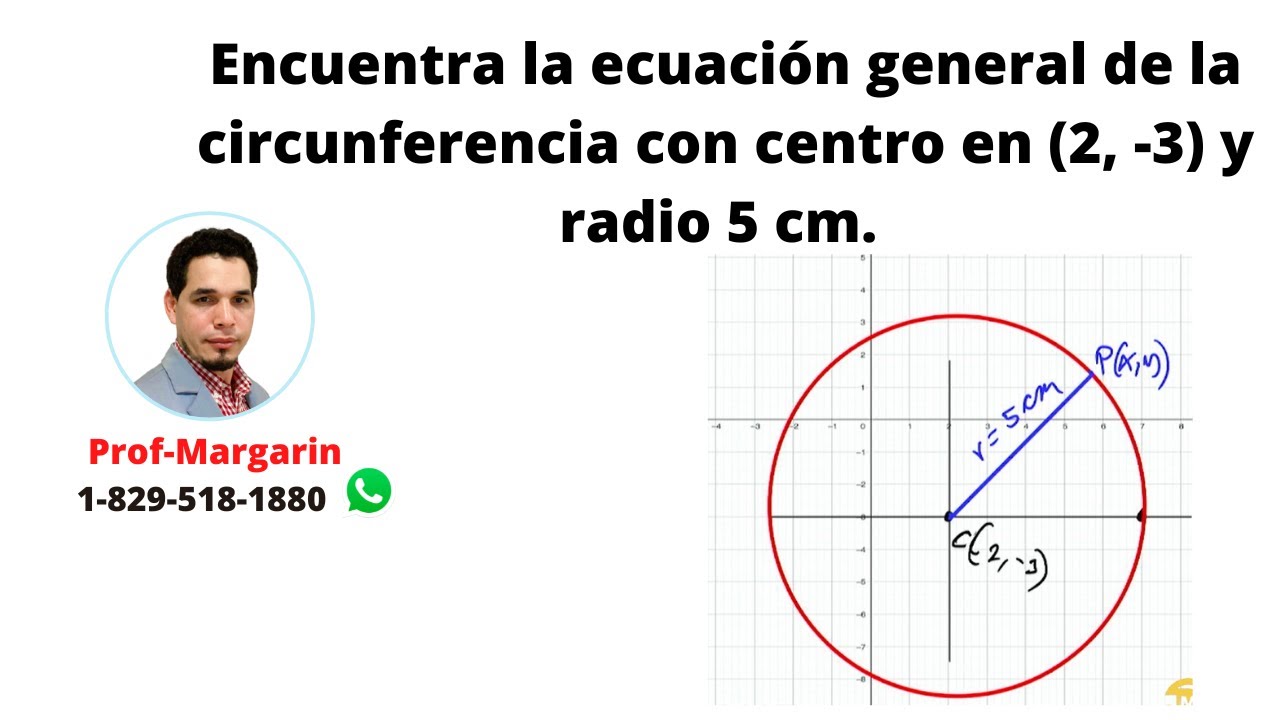
En esta guía, exploraremos paso a paso cómo encontrar la ecuación general de una circunferencia con un centro dado en el punto (2, -3) y un radio de 5 unidades.
Conceptos básicos de la ecuación de una circunferencia
La ecuación de una circunferencia en el plano cartesiano se puede representar en forma general como:
(x – h)2 + (y – k)2 = r2
Donde (h, k) representa las coordenadas del centro de la circunferencia y r es el radio.
Paso 1: Identificar las coordenadas del centro y el radio
Para encontrar la ecuación general de la circunferencia, primero necesitamos identificar las coordenadas del centro (h, k) y el radio (r).
Centro de la circunferencia
En este caso, el centro de la circunferencia está ubicado en el punto (2, -3).
Radio de la circunferencia
El radio de la circunferencia es 5 unidades, lo que significa que la distancia desde el centro hasta cualquier punto de la circunferencia es 5 unidades.
Paso 2: Utilizar las coordenadas del centro y el radio en la ecuación general
Una vez que tenemos las coordenadas del centro y el radio, podemos usar la ecuación general de la circunferencia para encontrar la ecuación específica para este caso.
Entonces, sustituimos (h, k) = (2, -3) y r = 5 en la ecuación general:
(x – 2)2 + (y + 3)2 = 52
Paso 3: Expandir y simplificar la ecuación
Para encontrar la ecuación general, expandimos y simplificamos la ecuación obtenida en el paso anterior.
Al expandir los cuadrados y simplificar, la ecuación general de la circunferencia se convierte en:
x2 – 4x + 4 + y2 + 6y + 9 = 25
Combinando términos semejantes, obtenemos:
x2 + y2 – 4x + 6y – 12 = 0
Por lo tanto, la ecuación general de la circunferencia con centro en (2, -3) y radio 5 es x2 + y2 – 4x + 6y – 12 = 0.
Al seguir estos pasos, podemos encontrar la ecuación general de una circunferencia con cualquier centro y radio dados en el plano cartesiano.