La ley de cosenos es una herramienta fundamental en trigonometría para calcular la longitud de un lado de un triángulo cualquiera cuando se conocen las longitudes de los otros dos lados y el ángulo entre ellos. Esta ley es especialmente útil en situaciones donde se necesita encontrar distancias o ángulos en geometría, navegación, ingeniería y física. En este artículo, exploraremos varias situaciones en las que la ley de cosenos encuentra aplicaciones prácticas.
En la navegación marítima, la ley de cosenos es fundamental para calcular la distancia entre dos puntos en la superficie de la Tierra cuando se conoce la latitud y longitud de ambos puntos. Considerando la curvatura de la Tierra, esta ley proporciona una forma precisa de determinar distancias que son esenciales para trazar rutas marítimas seguras y eficientes.
La ingeniería civil y la ley de cosenos
En el campo de la ingeniería civil, la ley de cosenos se utiliza para calcular fuerzas y momentos en estructuras que están sujetas a cargas externas. Al comprender las componentes de fuerza en diferentes ángulos, los ingenieros pueden diseñar y evaluar la estabilidad y resistencia de puentes, edificios y otros proyectos de construcción.
Aplicaciones en el análisis de movimiento
La ley de cosenos también se aplica en el análisis de movimiento, específicamente en el cálculo de la velocidad y aceleración de un objeto en un sistema de coordenadas tridimensional. Al descomponer la velocidad y el movimiento en sus componentes vectoriales, es posible utilizar la ley de cosenos para determinar la dirección y magnitud de estas variables en diferentes puntos del movimiento.
Aspectos matemáticos de la ley de cosenos
Para comprender plenamente la aplicación de la ley de cosenos en diferentes contextos, es fundamental tener un conocimiento claro de su formulación matemática. La ley de cosenos puede expresarse de varias formas, como la fórmula estándar que relaciona los lados y ángulos de un triángulo, o en términos de sus componentes vectoriales en un sistema coordenado tridimensional.
Fórmula estándar de la ley de cosenos
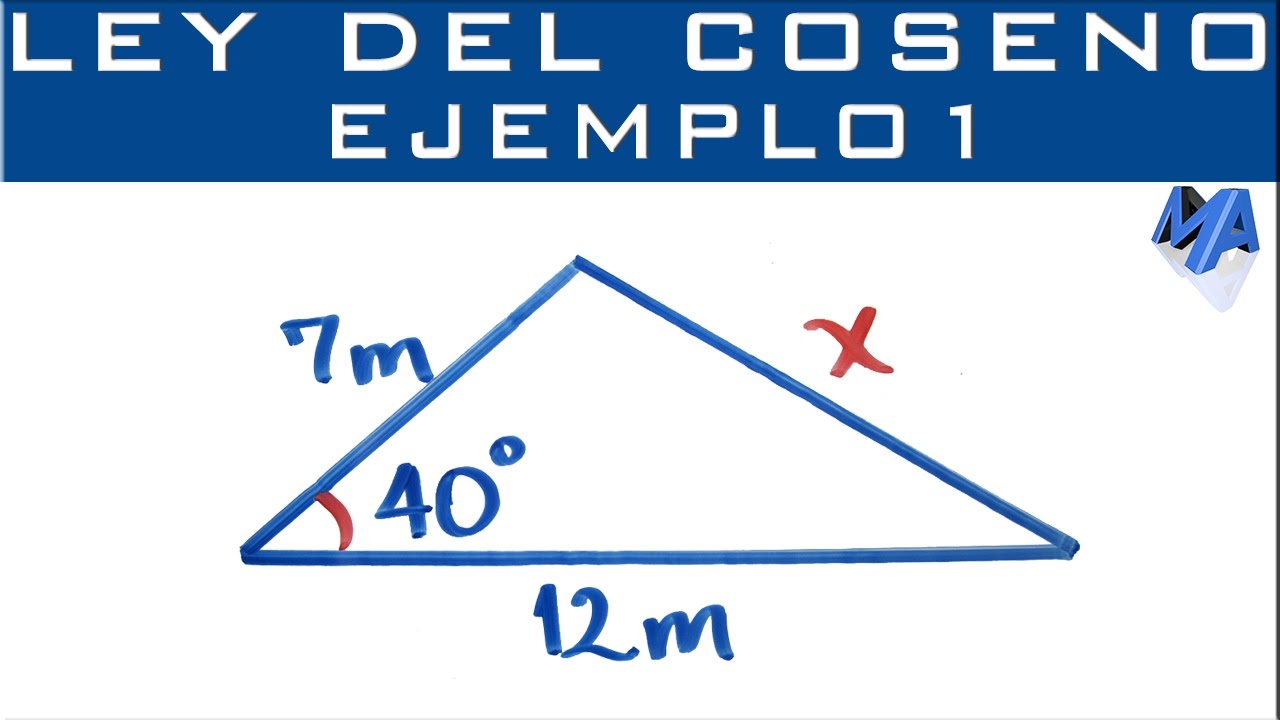
La fórmula estándar de la ley de cosenos se expresa como: c^2 = a^2 + b^2 – 2ab * cos(C), donde c es la longitud del lado opuesto al ángulo C, y a y b son las longitudes de los otros dos lados. Esta formulación es clave para calcular la longitud de un lado desconocido en un triángulo, dado que conocemos las longitudes de los otros dos lados y el ángulo entre ellos.
Componentes vectoriales y la ley de cosenos
En un sistema de coordenadas tridimensional, la ley de cosenos se extiende para calcular las proyecciones de un vector en direcciones específicas. Esto es esencial en el análisis de movimiento y fuerza en física y ingeniería, donde se requiere descomponer vectores en sus componentes rectangulares y determinar ángulos y magnitudes resultantes.
Aplicaciones prácticas en geodesia
La geodesia es la ciencia que se ocupa de la forma y dimensiones de la Tierra, y la medición de áreas y distancias en su superficie. La ley de cosenos encuentra aplicaciones significativas en este campo, especialmente en la determinación de distancias geodésicas y construcción de mapas precisos.
Cálculo de distancias geodésicas
Al considerar la curvatura de la Tierra, los geodestas utilizan la ley de cosenos para calcular distancias geodésicas entre dos puntos en su superficie. Este cálculo es esencial para la cartografía y la creación de sistemas de coordenadas geográficas que son fundamentales en la navegación y SIG (Sistemas de Información Geográfica).
Construcción de mapas precisos
La ley de cosenos se utiliza en la proyección cartográfica para transformar coordenadas geográficas esféricas en planas. Al comprender las relaciones angulares y de distancia entre los puntos en la superficie terrestre, los cartógrafos pueden representar de manera precisa el mundo tridimensional en mapas bidimensionales para una amplia gama de aplicaciones.
La ley de cosenos es una poderosa herramienta matemática con aplicaciones prácticas en diversos campos de la ciencia y la ingeniería. Desde la navegación marítima hasta la geodesia, su capacidad para calcular distancias, ángulos y fuerzas es fundamental para resolver problemas del mundo real. Al comprender sus fundamentos matemáticos y su aplicación en diferentes contextos, es posible utilizar la ley de cosenos de manera efectiva en múltiples situaciones, contribuyendo al avance y desarrollo de diversas disciplinas.