En el cálculo diferencial, las derivadas juegan un papel fundamental al medir la tasa de cambio instantánea de una función en relación con su variable independiente. Este concepto es esencial en gran cantidad de disciplinas científicas, desde la física y la ingeniería hasta la economía y la biología, ya que permite analizar el comportamiento de sistemas y resolver problemas de optimización.
Dos tipos de funciones que se encuentran frecuentemente en estas aplicaciones son las funciones exponenciales y logarítmicas. Las funciones exponenciales tienen la forma general f(x) = a^x, donde a es una constante positiva. Por otro lado, las funciones logarítmicas tienen la forma general f(x) = log_a(x), donde a es una base positiva distinta de 1. Estas funciones se caracterizan por su crecimiento o decrecimiento rápido y permiten modelar fenómenos como el crecimiento de poblaciones, decaimiento radioactivo o la capacidad de almacenamiento de información en computadoras.
Derivadas de funciones exponenciales
Definición de la función exponencial
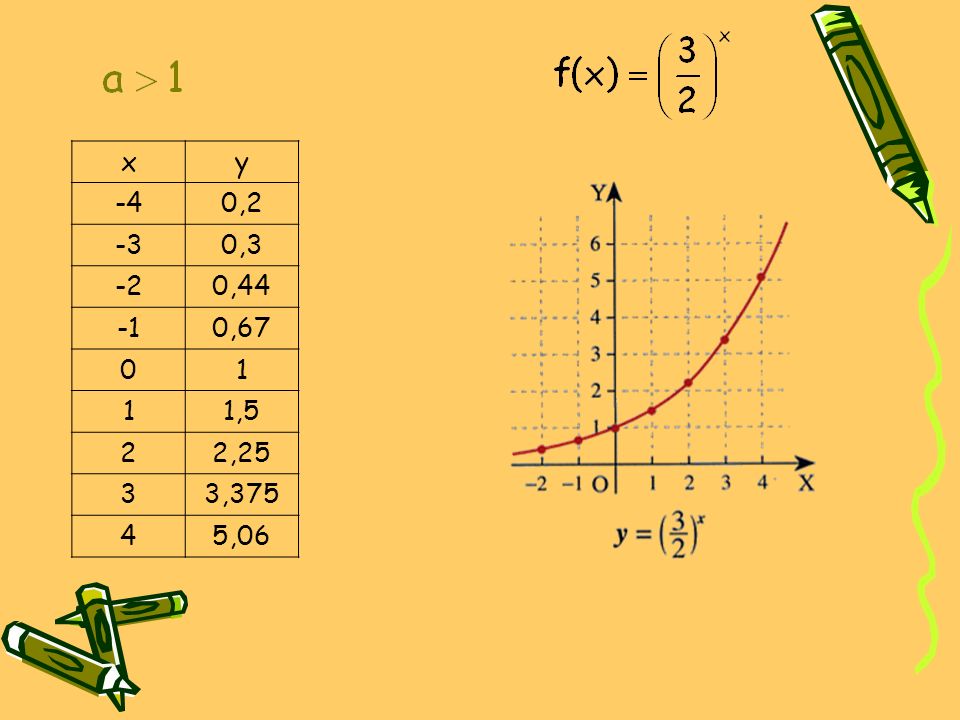
La función exponencial se define como una función en la que la variable independiente x se encuentra en el exponente. Su forma general es f(x) = a^x, donde a es una constante positiva. Cuando a es igual a la base del logaritmo natural, e ≈ 2.71828, se tiene una función exponencial especial conocida como función exponencial natural, f(x) = e^x.
Propiedades de las funciones exponenciales
Las funciones exponenciales tienen varias propiedades importantes que permiten comprender su comportamiento. Algunas de estas propiedades incluyen:
- Crecimiento exponencial: Las funciones exponenciales crecen rápidamente a medida que x se acerca al infinito.
- Decrecimiento exponencial: Las funciones exponenciales con 0 < a < 1 disminuyen rápidamente a medida que x se acerca al infinito.
- Relación entre la base y el crecimiento de la función: Una base mayor a amplifica el crecimiento exponencial, mientras que una base menor a disminuye el crecimiento.
Regla de la cadena para derivadas de funciones exponenciales
La regla de la cadena es una regla fundamental en el cálculo diferencial que permite derivar funciones compuestas. Para derivar una función exponencial compuesta, como f(g(x)), la regla de la cadena establece que se debe multiplicar la derivada de la función externa (f’) por la derivada de la función interna (g’). La derivada de una función exponencial a^x es que f'(x) = ln(a) * a^x.
Derivadas de funciones logarítmicas
Definición de la función logarítmica
La función logarítmica se define como la inversa de una función exponencial. Su forma general es f(x) = log_a(x), donde a es la base del logaritmo y x es un número positivo. El logaritmo natural, ln(x), es una función logarítmica especial en base a = e.
Propiedades de las funciones logarítmicas
Las funciones logarítmicas también tienen varias propiedades importantes que ayudan a comprender su comportamiento. Algunas de estas propiedades incluyen:
- Dominio y rango: El dominio de una función logarítmica es el conjunto de números positivos y el rango puede ser todo el conjunto de números reales.
- Relación entre la base y el comportamiento de la función: Una base mayor a hace que la función logarítmica crezca más rápidamente, mientras que una base menor a hace que la función crezca más lentamente.
- Propiedad del cambio de base: La función logarítmica se puede expresar con cualquier base b usando la fórmula log_b(x) = log_a(x) / log_a(b).
Regla de la cadena para derivadas de funciones logarítmicas
Al igual que con las funciones exponenciales, la regla de la cadena también se aplica para derivar funciones logarítmicas compuestas. Para derivar una función logarítmica compuesta, f(g(x)), la regla de la cadena establece que se debe multiplicar la derivada de la función externa (f’) por la derivada de la función interna (g’). La derivada de una función logarítmica log_a(x) es f'(x) = 1 / (x * ln(a)).
Ejemplos de derivadas de funciones exponenciales y logarítmicas
Derivadas de funciones exponenciales simples
Para entender cómo derivar funciones exponenciales, consideremos ejemplos específicos:
Ejemplo 1: Derivada de f(x) = 3^x
Aplicando la regla de la cadena, obtenemos f'(x) = ln(3) * 3^x.
Ejemplo 2: Derivada de f(x) = e^(2x)
Aplicando la regla de la cadena, obtenemos f'(x) = 2 * e^(2x).
Derivadas de funciones logarítmicas simples
Consideremos ejemplos específicos para comprender cómo derivar funciones logarítmicas:
Ejemplo 1: Derivada de f(x) = log_2(x)
Aplicando la regla de la cadena, obtenemos f'(x) = 1 / (x * ln(2)).
Ejemplo 2: Derivada de f(x) = ln(3x)
Aplicando la regla de la cadena, obtenemos f'(x) = 1 / x.
Derivadas de combinaciones de funciones exponenciales y logarítmicas
También podemos derivar funciones que son combinaciones de funciones exponenciales y logarítmicas:
Ejemplo: Derivada de f(x) = e^(2x) + ln(x)
Aplicando la regla de la cadena, obtenemos f'(x) = 2 * e^(2x) + 1 / x.
Aplicaciones de las derivadas de funciones exponenciales y logarítmicas
Modelado de crecimiento y decaimiento
Las funciones exponenciales y logarítmicas son ampliamente utilizadas para modelar situaciones de crecimiento y decaimiento en varios campos científicos y técnicos. Por ejemplo, en biología, pueden utilizarse para describir el crecimiento de poblaciones. En economía, pueden utilizarse para modelar el crecimiento de inversiones. En física, pueden utilizarse para describir el decaimiento radioactivo.
Resolución de problemas de optimización
Las derivadas de funciones exponenciales y logarítmicas también son útiles para resolver problemas de optimización, es decir, encontrar el máximo o mínimo valor de una función sujeta a ciertas restricciones. Estos problemas se pueden plantear como maximizar o minimizar una función objetivo bajo ciertas restricciones y la derivación es una herramienta clave para encontrar la solución óptima.
Las derivadas de funciones exponenciales y logarítmicas son conceptos fundamentales en el cálculo diferencial con una amplia gama de aplicaciones en diversos campos científicos y tecnológicos. Comprender y aplicar estas derivadas permite modelar fenómenos de crecimiento y decaimiento, así como resolver problemas de optimización. A lo largo de este artículo, hemos analizado en detalle las definiciones, propiedades y reglas de derivación de estas funciones, además de proporcionar ejemplos prácticos para ilustrar su aplicación. Esperamos que este artículo haya proporcionado una comprensión completa de las derivadas de funciones exponenciales y logarítmicas.