1. Introducción a la distribución binomial
La distribución binomial es uno de los conceptos fundamentales en la teoría de la probabilidad y estadística. Se utiliza para modelar el resultado de una serie de experimentos independientes, donde cada experimento tiene dos posibles resultados: éxito o fracaso.
La distribución binomial se puede utilizar en una variedad de situaciones, como por ejemplo, calcular la probabilidad de obtener un número específico de éxitos en un número determinado de intentos.
Características de la distribución binomial
La distribución binomial se caracteriza por los siguientes aspectos:
- Número de ensayos: Se refiere al número de experimentos independientes que se realizarán.
- Probabilidad de éxito: Es la probabilidad de que ocurra un éxito en cada experimento individual.
- Probabilidad de fracaso: Es la probabilidad de que ocurra un fracaso en cada experimento individual.
- Independencia de los ensayos: Cada ensayo o experimento se considera independiente, lo que significa que el resultado de un ensayo no afecta el resultado de los demás.
Fórmula de la distribución binomial
La fórmula general para calcular la probabilidad de obtener exactamente x éxitos en n ensayos, con una probabilidad de éxito de p, es:
P(X = x) = (nCx) * p^x * (1-p)^(n-x)
Donde nCx representa el coeficiente binomial, que se calcula como:
nCx = n! / (x! * (n-x)!)
Esta fórmula permite calcular la probabilidad de obtener cualquier número específico de éxitos en una serie de ensayos.
Ejemplo de distribución binomial
Supongamos que lanzamos una moneda justa 10 veces. Queremos calcular la probabilidad de obtener exactamente 5 caras.
Utilizando la fórmula de la distribución binomial, podemos calcular:
P(X = 5) = (10C5) * (0.5^5) * (0.5^5) = 0.246
Por lo tanto, la probabilidad de obtener exactamente 5 caras en 10 lanzamientos de una moneda justa es de aproximadamente 0.246.
2. Introducción a la distribución normal
En el campo de la estadística, la distribución normal es una de las distribuciones más importantes y ampliamente utilizadas. También conocida como distribución de Gauss o campana de Gauss, esta distribución es simétrica y tiene una forma de campana.
La distribución normal se caracteriza por tener una media y una desviación estándar.
La media de la distribución normal representa el centro de la campana, mientras que la desviación estándar determina la “anchura” de la campana. En esta distribución, aproximadamente el 68% de los datos caen dentro de una desviación estándar de la media, el 95% caen dentro de dos desviaciones estándar y el 99.7% caen dentro de tres desviaciones estándar.
La distribución normal tiene propiedades matemáticas y estadísticas muy útiles, lo que la convierte en una herramienta fundamental en el análisis de datos y la toma de decisiones. Se utiliza en investigaciones científicas, análisis de mercado, pronósticos y muchas otras áreas.
Características de la distribución normal:
- Simetria: La distribución es simétrica alrededor de su media.
- Forma de campana: La distribución tiene una forma similar a una campana.
- Media y desviación estándar: La distribución se define por su media y desviación estándar.
- Curva continua: La distribución es una curva continua sin puntos discretos.
En resumen, la distribución normal es una poderosa herramienta en el análisis estadístico. Su forma de campana y propiedades matemáticas la hacen muy útil en diversos campos. Entender la distribución normal es fundamental para cualquier persona que trabaje con datos y análisis estadístico.
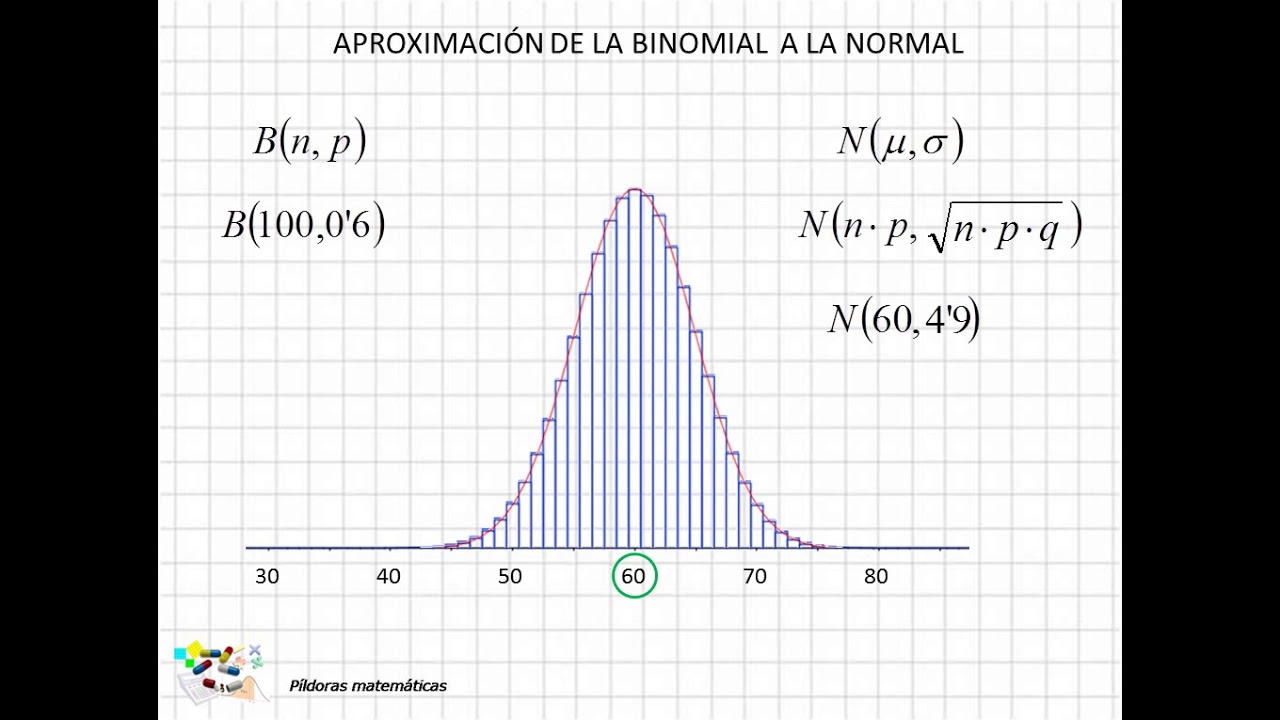
3. Aproximación de la distribución binomial a la normal
La aproximación de la distribución binomial a la normal es un concepto fundamental en la teoría de probabilidades y estadísticas. Permite simplificar cálculos complejos y hacer estimaciones más precisas en determinadas situaciones.
La distribución binomial es una distribución de probabilidad discreta que modela el número de éxitos en una serie de ensayos independientes y idénticamente distribuidos. Se caracteriza por tener dos parámetros: el número de ensayos (n) y la probabilidad de éxito en cada ensayo (p).
La distribución normal, por otro lado, es una distribución de probabilidad continua que se caracteriza por tener una forma de campana simétrica. Su media y desviación estándar determinan completamente su forma.
En ciertas circunstancias, cuando el número de ensayos (n) es grande y la probabilidad de éxito (p) no es ni muy cercana a 0 ni muy cercana a 1, la distribución binomial se puede aproximar a la distribución normal. Esto es conocido como teorema del límite central.
La aproximación se puede justificar matemáticamente mediante la aplicación del teorema de Moivre-Laplace y utilizando la función de densidad de la distribución normal. La aproximación es más precisa a medida que el número de ensayos aumenta.
La aproximación de la distribución binomial a la normal permite simplificar cálculos al utilizar las propiedades conocidas de la distribución normal, como la suma de variables aleatorias independientes.
Esta aproximación es útil en diversos campos, como la ingeniería, la economía y la biología, donde se realizan experimentos con múltiples ensayos independientes. También es aplicable en estudios epidemiológicos o encuestas de opinión, donde se desea estimar la proporción de una característica en una población.
- La aproximación de la distribución binomial a la normal es un concepto fundamental en la teoría de probabilidades y estadísticas.
- La distribución binomial es una distribución de probabilidad discreta que modela el número de éxitos en una serie de ensayos independientes y idénticamente distribuidos.
- La distribución normal es una distribución de probabilidad continua que se caracteriza por tener una forma de campana simétrica.
- En ciertas circunstancias, cuando el número de ensayos es grande y la probabilidad de éxito no es muy cercana a 0 ni muy cercana a 1, la distribución binomial se puede aproximar a la distribución normal.
- La aproximación se puede justificar matemáticamente mediante la aplicación del teorema de Moivre-Laplace y utilizando la función de densidad de la distribución normal.
- La aproximación de la distribución binomial a la normal permite simplificar cálculos al utilizar las propiedades conocidas de la distribución normal.
- Esta aproximación es útil en diversos campos, como la ingeniería, la economía y la biología.
4. Ventajas y limitaciones de la aproximación
La aproximación tiene varias ventajas que la hacen atractiva para diversos casos de uso:
1. Rapidez
La aproximación permite obtener resultados de forma más rápida en comparación con otros métodos más complejos. Esto es especialmente útil cuando se necesita una respuesta rápida o se trabaja con grandes volúmenes de datos.
2. Facilidad de implementación
La aproximación no requiere conocimientos avanzados en matemáticas o algoritmos complicados. Esto significa que cualquier persona con un nivel básico de programación puede implementarla sin inconvenientes.
3. Flexibilidad
La aproximación se puede adaptar fácilmente a diferentes escenarios y problemas. Esto permite su uso en una amplia variedad de aplicaciones, desde análisis de datos hasta procesamiento de imágenes.
A pesar de estas ventajas, también existen algunas limitaciones asociadas a la aproximación:
1. Precisión limitada
La aproximación puede producir resultados aproximados en lugar de valores exactos. Esto puede ser un problema en casos donde se requiere una alta precisión, como en cálculos científicos o financieros.
2. Dependencia del conjunto de datos
La calidad de los resultados obtenidos mediante la aproximación puede depender del conjunto de datos utilizado. En algunos casos, es posible que la aproximación funcione bien para un conjunto de datos específico pero no para otros.
3. Dificultad para interpretar los resultados
En algunos casos, la aproximación puede generar resultados difíciles de interpretar. Esto puede ser problemático si se necesitan análisis detallados o explicaciones claras de los resultados obtenidos.
A pesar de estas limitaciones, la aproximación sigue siendo una herramienta útil en muchos casos y puede proporcionar resultados satisfactorios en la mayoría de las situaciones.
5. Conclusiones
En este artículo, hemos discutido varios temas relacionados con la importancia de utilizar etiquetas HTML para resaltar la información más relevante en un texto.
En primer lugar, hemos aprendido sobre las etiquetas HTML <strong> las cuales se utilizan para hacer que un texto se vea en negrita. Esto es especialmente útil para resaltar las frases o palabras clave en un párrafo, haciendo que se destaquen y sean más fácilmente identificables para el lector.
Además, hemos explorado la opción de utilizar la etiqueta HTML <h3> para crear subtítulos en nuestro texto. Esto no solo ayuda a organizar la información de manera más clara, sino que también permite al lector identificar rápidamente los puntos clave dentro de un artículo.
Otra herramienta que hemos mencionado son las listas en HTML. Estas nos permiten presentar información de manera estructurada y ordenada. Podemos utilizar las etiquetas <ul> y <li> para crear listas no ordenadas, o las etiquetas <ol> y <li> para crear listas ordenadas. En ambos casos, podemos utilizar la etiqueta <strong> para hacer que los elementos de la lista se vean en negrita y así resaltarlos.
En conclusión, el uso de etiquetas HTML como <strong>, <h3> y listas es fundamental para mejorar la legibilidad y la organización de nuestros textos web. Al resaltar las frases importantes, utilizar subtítulos claros y presentar la información de forma estructurada, facilitamos la comprensión del contenido por parte del lector y hacemos que la lectura sea más agradable y efectiva.