La función hipergeométrica es una herramienta matemática poderosa que se utiliza en una variedad de campos, desde la física hasta la estadística. Sin embargo, en algunos casos, la función hipergeométrica puede resultar difícil de manejar o calcular. En tales situaciones, la aproximación de la función hipergeométrica mediante la función binomial puede ofrecer una solución más accesible y práctica.
El poder de la aproximación binomial
Cuando nos enfrentamos a la complejidad de la función hipergeométrica, es crucial encontrar métodos alternativos que nos permitan obtener resultados aproximados de manera más efectiva. Aquí es donde entra en juego la función binomial, ofreciendo una perspectiva diferente para abordar problemas que involucran la función hipergeométrica.
Entendiendo la función hipergeométrica
Antes de sumergirnos en la aproximación mediante la función binomial, es fundamental comprender qué es la función hipergeométrica y cuándo se utiliza. La función hipergeométrica se define como una serie infinita que surge en el contexto de combinatoria y probabilidad. Se utiliza para representar la probabilidad de obtener un cierto número de éxitos en una secuencia de ensayos donde cada ensayo tiene dos posibles resultados y la probabilidad de éxito en cada ensayo es constante.
Evaluación de la función hipergeométrica
Calcular la función hipergeométrica puede ser desafiante, especialmente cuando se trata de casos con numerosos ensayos o combinaciones complejas. La complejidad computacional asociada con la función hipergeométrica puede limitar su aplicabilidad en situaciones prácticas, lo que nos lleva a explorar métodos alternativos para obtener resultados útiles.
El enfoque de aproximación binomial
Cuando nos encontramos con situaciones en las que la función hipergeométrica presenta dificultades para su evaluación precisa, la aproximación mediante la función binomial ofrece una solución práctica y manejable. La función binomial, que representa la probabilidad de obtener un número específico de éxitos en un cierto número de ensayos independientes, se convierte en una herramienta valiosa para obtener una aproximación cercana a la función hipergeométrica.
Aplicación de la función binomial
La clave para usar la función binomial como una herramienta de aproximación para la función hipergeométrica radica en la identificación de condiciones en las que ambos enfoques proporcionan resultados comparables. Al comprender las similitudes y diferencias entre ambas funciones, podemos determinar cuándo es apropiado utilizar la función binomial para obtener una aproximación efectiva de la función hipergeométrica.
Comparación de resultados
Una parte fundamental del proceso de aproximación es comparar los resultados obtenidos mediante la función binomial con los valores reales de la función hipergeométrica. Esta comparación nos permite evaluar la precisión y la utilidad de la aproximación, y nos brinda información importante sobre la validez de utilizar la función binomial en lugar de la función hipergeométrica en determinadas circunstancias.
Visualización de datos
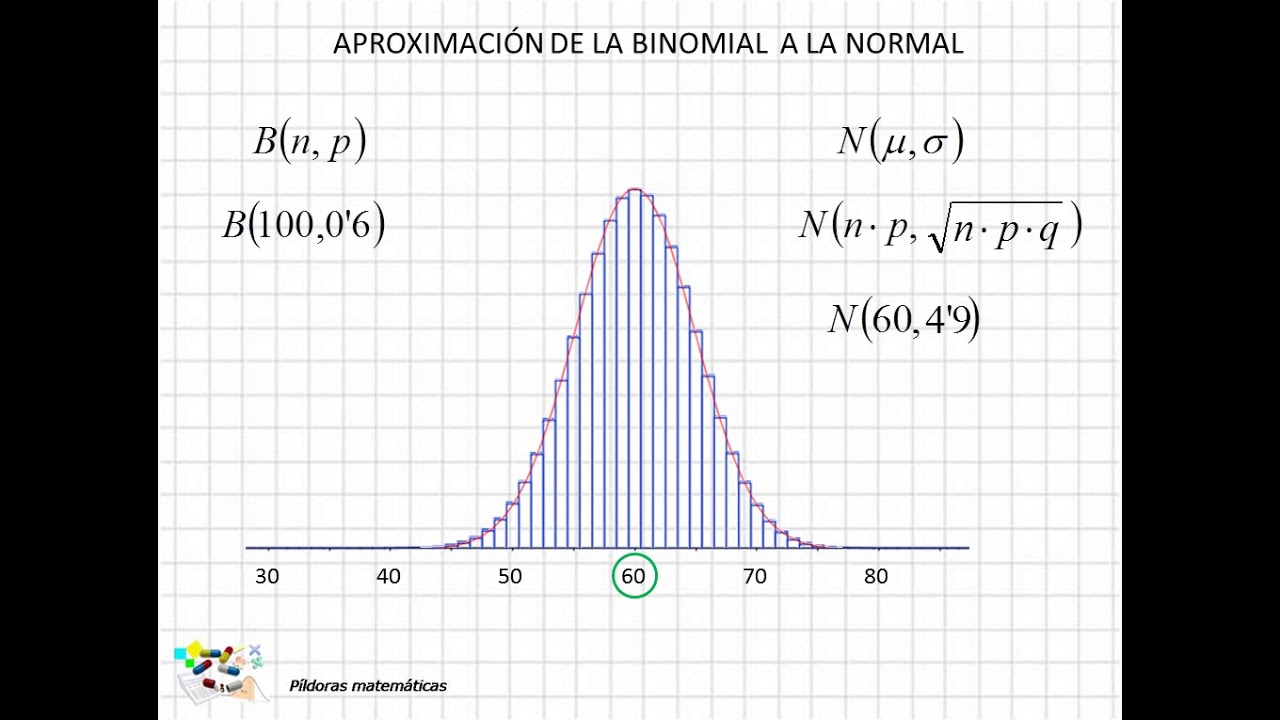
Para ilustrar la comparación entre la función hipergeométrica y su aproximación mediante la función binomial, es útil recurrir a visualizaciones de datos que nos permitan observar la convergencia o divergencia de ambos enfoques en diferentes contextos. El uso de gráficos y diagramas puede ofrecer una perspectiva más clara sobre la eficacia de la aproximación binomial en la práctica.
Consideraciones de precisión y validez
A medida que exploramos el potencial de la aproximación de la función hipergeométrica mediante la función binomial, es esencial tener en cuenta las limitaciones y condiciones para garantizar la precisión y validez de esta técnica. La precisión de la aproximación depende en gran medida de la elección cuidadosa de los parámetros y del contexto en el que se aplica, y es crucial considerar estas consideraciones para obtener resultados significativos.
Validación de la aproximación
Validar la aproximación mediante la función binomial implica someterla a pruebas rigurosas y comparar los resultados con casos de referencia o soluciones conocidas de la función hipergeométrica. Este proceso de validación nos permite determinar la confiabilidad y utilidad de la aproximación en diferentes escenarios, proporcionando una base sólida para su aplicación en situaciones prácticas.
Aplicaciones prácticas
Finalmente, es crucial explorar las aplicaciones prácticas de la aproximación de la función hipergeométrica mediante la función binomial en diversos campos, como la estadística, la ingeniería y la investigación científica. Identificar escenarios específicos en los que la aproximación binomial ofrece ventajas significativas nos permite aprovechar al máximo esta técnica en entornos del mundo real.
Beneficios en la resolución de problemas
Al enfocarse en los beneficios concretos que la aproximación binomial puede aportar a la resolución de problemas prácticos, se destaca su relevancia y utilidad en la toma de decisiones informadas y en la modelización precisa de fenómenos complejos. La capacidad de obtener resultados aproximados de manera eficiente y efectiva impulsa la aplicación de esta aproximación en una variedad de situaciones cotidianas.
En conclusión, la aproximación de la función hipergeométrica mediante la función binomial emerge como una herramienta matemática valiosa que ofrece soluciones prácticas a problemas complejos. Al comprender las condiciones de aplicación, considerar la precisión y validar la aproximación, podemos aprovechar el potencial de la función binomial para obtener resultados aproximados de manera efectiva en una amplia gama de escenarios.