«`html
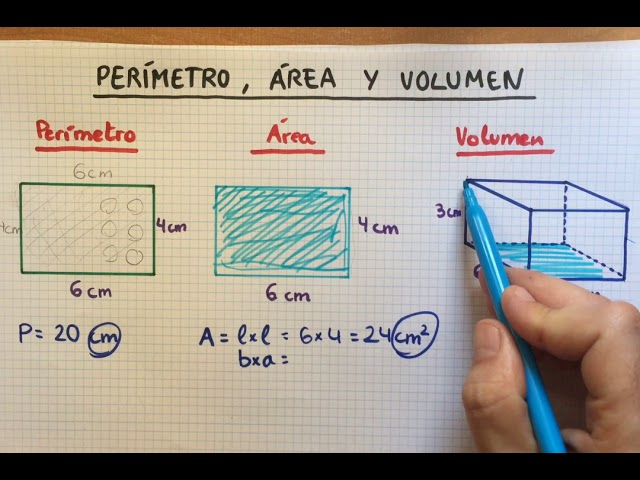
Descubre las fórmulas para calcular áreas y volúmenes
«`
Calcular áreas y volúmenes de figuras geométricas puede parecer desafiante, pero con las fórmulas correctas y un poco de práctica, ¡puedes dominar este aspecto crucial de las matemáticas! En este artículo, exploraremos paso a paso cómo calcular áreas y volúmenes de diversas figuras geométricas, desde triángulos y cuadrados, hasta esferas y cilindros. Prepárate para adentrarte en el apasionante mundo de la geometría y descubrir las herramientas para resolver cualquier problema que se te presente.
«`html
Cálculo del área de figuras bidimensionales
«`
Comencemos por comprender cómo calcular el área de figuras bidimensionales, como triángulos, cuadrados, rectángulos y círculos. El área es la cantidad de superficie que abarca una figura, y para cada tipo de figura existe una fórmula específica que nos permite realizar este cálculo de manera precisa. Vamos a sumergirnos en las fórmulas clave y ver cómo aplicarlas en ejemplos prácticos para comprender mejor su utilidad.
«`html
Triángulos: fórmula de área de Herón
«`
El área de un triángulo se puede calcular utilizando la fórmula de Herón, que requiere conocer las medidas de los tres lados del triángulo. Una vez que tengas estas medidas, puedes utilizar la siguiente fórmula para encontrar el área:
[ A = sqrt{s(s-a)(s-b)(s-c)} ]
donde «s» es el semiperímetro del triángulo, es decir, la mitad de la suma de los tres lados, y «a», «b», y «c» son las longitudes de los lados del triángulo. Este método es especialmente útil cuando conoces todas las medidas de los lados y necesitas encontrar el área sin conocer la altura.
«`html
Cuadrados y rectángulos: multiplicación de lados
«`
Para encontrar el área de un cuadrado o un rectángulo, simplemente multiplica la longitud de un lado por la longitud del lado adyacente. Por ejemplo, si tienes un cuadrado con lados de longitud 4 unidades, el área sería 16 unidades cuadradas ((A = l times l = l^2)). Esta fórmula también se aplica a los rectángulos, donde la longitud y la anchura pueden ser diferentes.
«`html
Círculos: fórmula de área usando el radio
«`
El área de un círculo se puede calcular utilizando la fórmula:
[ A = pi times r^2 ]
donde «r» es el radio del círculo. Aquí, «π» es una constante que aproximadamente equivale a 3.14159. Simplemente eleva al cuadrado el radio del círculo y multiplica el resultado por «π» para encontrar el área. Esta fórmula es muy útil en situaciones donde necesitas encontrar el área de un círculo, ya sea para proyectos de construcción, artesanía o simplemente por el placer de resolver problemas matemáticos.
«`html
Determinación de volúmenes de figuras tridimensionales
«`
Ahora que hemos explorado el cálculo de áreas para figuras bidimensionales, es hora de adentrarnos en el emocionante mundo de los volúmenes de figuras tridimensionales. Desde cubos y esferas hasta conos y cilindros, cada figura tridimensional tiene su propia fórmula específica para calcular el espacio que ocupa en el espacio tridimensional. ¡Sigamos adelante y descubramos cómo hacerlo!
«`html
Cubos y paralelepípedos: multiplicación de dimensiones
«`
Para encontrar el volumen de un cubo o un paralelepípedo, simplemente multiplica la longitud, el ancho y la altura. Este enfoque es simple y efectivo, proporcionándote el volumen de la figura tridimensional de manera directa. Por ejemplo, si tienes un cubo con lados de longitud 3 unidades, el volumen sería 27 unidades cúbicas ((V = l times a times h)).
«`html
Esferas: fórmula de volumen con el radio
«`
El volumen de una esfera se puede calcular utilizando la fórmula:
[ V = frac{4}{3} times pi times r^3 ]
donde «r» es el radio de la esfera. Al elevar el radio al cubo, multiplicarlo por (frac{4}{3}) y por «π», obtendrás el volumen de la esfera. Esta fórmula es crucial en campos como la ingeniería, la física y la fabricación de productos redondos, ya que permite calcular el espacio que ocupan las esferas de manera precisa.
«`html
Conos y cilindros: fórmulas específicas para cada figura
«`
Tanto los conos como los cilindros tienen fórmulas específicas para calcular su volumen, que varían en función de sus dimensiones. Por ejemplo, el volumen de un cono se puede calcular con la fórmula:
[ V = frac{1}{3} times pi times r^2 times h ]
donde «r» es el radio de la base del cono y «h» es la altura. Por otro lado, el volumen de un cilindro se puede encontrar con la fórmula:
[ V = pi times r^2 times h ]
donde «r» es el radio de la base del cilindro y «h» es la altura. Con estas fórmulas a tu disposición, podrás calcular el volumen de conos y cilindros con facilidad.
«`html
Aplicaciones prácticas y desafíos matemáticos
«`
Calcular áreas y volúmenes de figuras geométricas no solo es un ejercicio académico, sino que también tiene numerosas aplicaciones prácticas en el mundo real. Desde la construcción y la arquitectura hasta la ingeniería y el diseño, las habilidades para calcular áreas y volúmenes son esenciales para resolver problemas cotidianos y desafíos matemáticos. ¿Listo para poner a prueba tus habilidades? A continuación, te presentamos algunos ejemplos y desafíos matemáticos para que pongas en práctica tus conocimientos:
«`html
Desafío 1: Diseño de un parque infantil
«`
Imagina que tienes la tarea de diseñar un parque infantil con diferentes áreas de juegos. Necesitas calcular el área total disponible para distribuir eficientemente los juegos y las áreas de descanso. Utiliza tus habilidades matemáticas para calcular las áreas de las diversas secciones del parque y diseñar un espacio divertido y seguro para los niños.
«`html
Desafío 2: Optimización de materiales de construcción
«`
Un constructor necesita optimizar el uso de materiales al construir una serie de tanques de agua cilíndricos para una comunidad. Utilizando tus conocimientos en cálculo de volúmenes, ayúdalo a determinar las dimensiones óptimas de cada tanque para minimizar el desperdicio de materiales y maximizar la capacidad de almacenamiento.
«`html
Desafío 3: Creación de esculturas geométricas
«`
Un artista desea crear esculturas tridimensionales utilizando bloques de diferentes formas geométricas. Ayúdalo a calcular los volúmenes de los bloques para que pueda planificar la disposición y el diseño de sus esculturas con precisión matemática. ¿Cómo distribuirías los bloques para crear una composición equilibrada y estéticamente atractiva?
¡Es hora de poner a prueba tus habilidades y desafiarte con situaciones del mundo real que requieren el cálculo preciso de áreas y volúmenes! Estos desafíos no solo te llevarán a aplicar tus conocimientos matemáticos, sino que también te proporcionarán una comprensión más profunda de la importancia y la relevancia de estas habilidades en diferentes entornos.
En conclusión, el cálculo de áreas y volúmenes de figuras geométricas es una habilidad fundamental que tiene aplicaciones prácticas y desafíos fascinantes. Desde fórmulas específicas para figuras bidimensionales hasta el desafío de aplicar estos conocimientos en situaciones del mundo real, dominar estas destrezas matemáticas te abrirá un mundo de posibilidades. ¡Sumérgete en el emocionante mundo de la geometría y descubre las maravillas que puedes crear con el poder de los números y las formas!
Espero que este artículo te haya inspirado a explorar más allá de los cálculos básicos y a desafiarte con problemas matemáticos emocionantes. ¡Sigue adelante y sigue explorando el sorprendente mundo de las figuras geométricas!