¿Qué es un hexágono?
Un hexágono es una figura geométrica plana que tiene seis lados y seis ángulos. Cada lado del hexágono es recto y mide lo mismo, y cada ángulo interno es igual a 120 grados.
La palabra “hexágono” proviene del griego “hex”, que significa seis, y “gonía”, que significa ángulo. Es una figura muy común en la naturaleza y se puede encontrar en muchas estructuras y formas, como los colmenares de las abejas y los cristales de nieve.
Características principales de un hexágono:
- Seis lados: Un hexágono tiene seis lados rectos que son iguales en longitud.
- Seis ángulos: Cada ángulo interno del hexágono mide 120 grados.
- Simetría: Un hexágono tiene múltiples ejes de simetría, lo que significa que se puede dividir en dos o más partes iguales.
- Área: El área de un hexágono se puede calcular multiplicando la longitud de uno de sus lados por el apotema (la distancia desde el centro del hexágono hasta uno de sus lados).
Los hexágonos son utilizados en muchos campos, como la arquitectura, la ingeniería y las matemáticas. En la arquitectura, por ejemplo, se pueden encontrar hexágonos en la construcción de cúpulas y mosaicos. En la naturaleza, los panales de abejas son un excelente ejemplo de la eficiencia y fuerza estructural de los hexágonos.
En resumen, un hexágono es una figura geométrica de seis lados y seis ángulos que se encuentra en muchos aspectos de la naturaleza y en diferentes áreas de estudio. Su forma única y su simetría lo convierten en un elemento importante en el diseño y la construcción.
Fórmula para calcular la suma de los ángulos de un hexágono
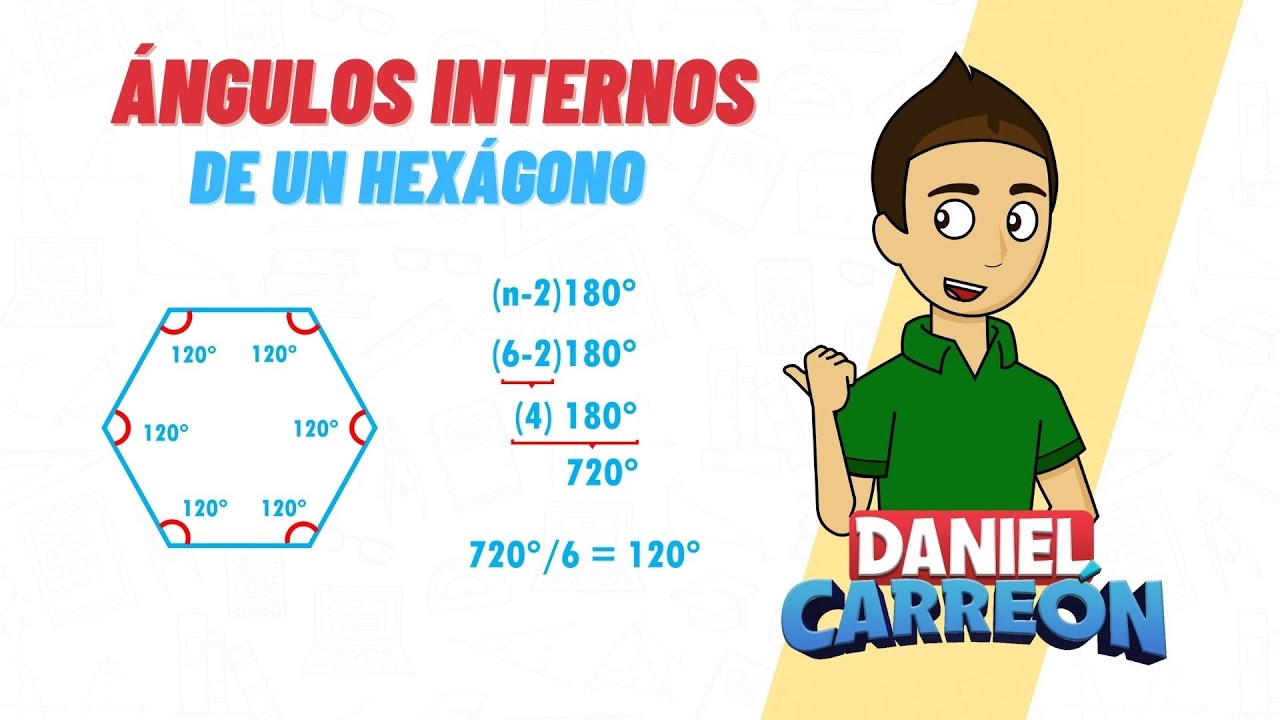
Un hexágono es un polígono con seis lados y seis ángulos. La suma de los ángulos de un hexágono se puede calcular utilizando la fórmula:
Suma de los ángulos de un hexágono = (n – 2) * 180 grados
donde “n” representa el número de lados del polígono, en este caso, seis.
Aplicando la fórmula, obtenemos:
Suma de los ángulos de un hexágono = (6 – 2) * 180 = 4 * 180 = 720 grados
Esta fórmula se puede aplicar no solo a hexágonos regulares, sino también a hexágonos irregulares. Sin embargo, en el caso de hexágonos irregulares, es importante recordar que los ángulos internos pueden tener diferentes tamaños y no ser todos iguales.
En resumen, la suma de los ángulos de un hexágono es de 720 grados. Recuerda esta fórmula cuando necesites calcular los ángulos de cualquier hexágono.
Importancia del cálculo de los ángulos de un hexágono
El cálculo de los ángulos de un hexágono es una tarea fundamental en geometría. Un hexágono es un polígono de seis lados y seis ángulos, y su conocimiento y comprensión es esencial en diversas áreas, como la arquitectura, la ingeniería y la ciencia.
Al conocer y calcular los ángulos de un hexágono, podemos determinar de manera precisa las propiedades y características de esta figura geométrica. Esto nos permite realizar diseños y construcciones eficientes y estables, ya que conocer los ángulos nos ayuda a distribuir equitativamente las fuerzas y las cargas.
¿Por qué es importante conocer los ángulos de un hexágono?
1. Estabilidad estructural: En la arquitectura y la ingeniería, conocer los ángulos de un hexágono es esencial para garantizar la estabilidad de estructuras como puentes, edificios y cualquier otra construcción. El cálculo preciso de los ángulos permite distribuir adecuadamente las fuerzas y evitar posibles colapsos o deformaciones.
2. Medición y trazado: En el campo del diseño y la construcción, el cálculo de los ángulos de un hexágono es crucial para realizar mediciones precisas y realizar trazados adecuados. Esto es especialmente importante en la carpintería, la fabricación de muebles y otros proyectos que requieren medidas exactas y ángulos precisos.
3. Aplicaciones científicas: En la ciencia, el cálculo de los ángulos de un hexágono es utilizado en áreas como la física, la química y la biología. Entender estos ángulos nos permite comprender mejor fenómenos naturales y procesos químicos, y aplicar esta información en investigaciones y experimentos.
Conclusiones
El cálculo de los ángulos de un hexágono es de suma importancia en diferentes áreas, ya que nos permite comprender y utilizar de manera eficiente esta figura geométrica. Su relevancia radica en la estabilidad estructural, las aplicaciones en diseño y construcción, y su utilidad en investigaciones científicas.
Ejemplo práctico del cálculo de los ángulos de un hexágono
En este post, te explicaré de manera práctica cómo calcular los ángulos de un hexágono. Un hexágono es un polígono de seis lados. Para poder obtener los ángulos de este polígono, necesitamos recordar que la suma de los ángulos interiores de cualquier polígono siempre es igual a (n-2) * 180 grados, donde n es el número de lados del polígono.
En el caso de un hexágono, n=6, por lo tanto, la suma de los ángulos interiores será (6-2) * 180 = 4 * 180 = 720 grados.
Como un hexágono tiene seis lados, cada uno de sus ángulos interiores será igual a la suma de los ángulos interiores dividida entre el número de lados, es decir, 720 / 6 = 120 grados.
Para visualizar mejor los ángulos de un hexágono, podemos trazar diagonales que dividen al hexágono en triángulos equiláteros. Un triángulo equilátero tiene todos sus ángulos iguales a 60 grados.
Por lo tanto, cada uno de los ángulos del hexágono puede ser considerado como la suma de dos ángulos de un triángulo equilátero contiguos. Esto nos indica que cada ángulo del hexágono medirá 120/2 = 60 grados.
Conclusiones
En resumen, las conclusiones más importantes de este texto son:
- El uso de etiquetas HTML es fundamental para dar formato y estructura a una página web.
- Las etiquetas H3 son muy útiles para resaltar títulos y subtitulos en un texto.
- Las listas en HTML, como la lista ordenada (ol) y lista desordenada (ul), permiten organizar información de manera clara y concisa.
- La etiqueta bold (b) es una forma sencilla de resaltar palabras o frases importantes en un texto.
Para crear contenido web de calidad, es importante conocer y utilizar estas herramientas en HTML de manera adecuada.