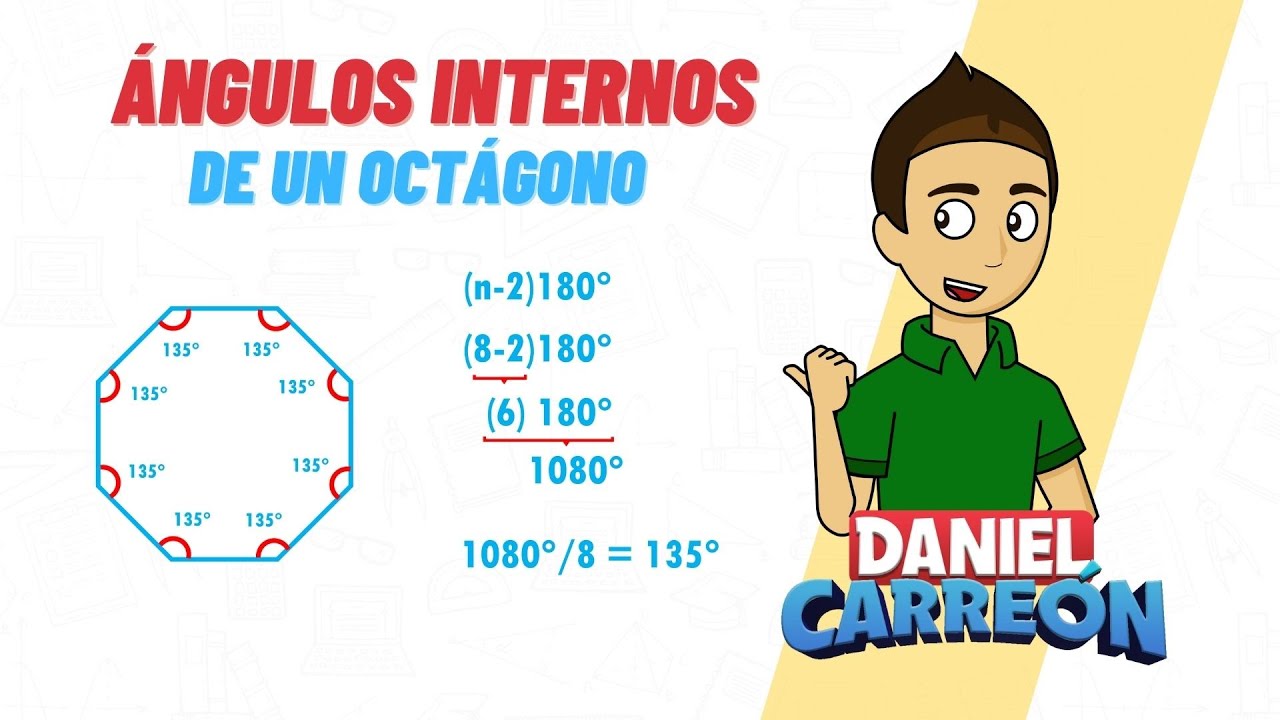
1. Definición de los ángulos internos
Los ángulos internos son aquellos que se forman en el interior de una figura geométrica. Se definen como la medida de la apertura entre dos líneas rectas que se encuentran en un punto común.
En un triángulo, por ejemplo, los ángulos internos se forman en cada uno de los vértices. La suma de los ángulos internos de un triángulo siempre es igual a 180 grados.
En un cuadrilátero, los ángulos internos se forman en cada uno de los cuatro vértices. La suma de los ángulos internos de un cuadrilátero siempre es igual a 360 grados.
En general, en una figura poligonal de n lados, la suma de los ángulos internos está dada por la fórmula (n-2)180 grados.
Es importante destacar que los ángulos internos pueden ser agudos (menores a 90 grados), rectos (iguales a 90 grados), obtusos (mayores a 90 grados) o también pueden ser llanos (iguales a 180 grados).
2. Cálculo de la medida de un ángulo interno
En Geometría, uno de los conceptos más importantes es el de los ángulos. Los ángulos se forman cuando dos rayos comparten un punto común llamado vértice.
Para calcular la medida de un ángulo interno, se utiliza la fórmula:
Medida del ángulo = 180° – Medida de los ángulos externos
Para entender esta fórmula, es necesario tener en cuenta que la suma de los ángulos internos de cualquier polígono es igual a (N – 2) multiplicado por 180°, donde N es el número de lados del polígono.
Por lo tanto, si conocemos la medida de los ángulos externos de un polígono, podemos restarla de 180° para encontrar la medida de los ángulos internos.
Veamos un ejemplo:
Ejemplo:
Tenemos un hexágono regular, es decir, un polígono de 6 lados iguales. Sabemos que la medida de los ángulos externos de este polígono es de 60°.
Aplicamos la fórmula:
Medida del ángulo = 180° – 60°
Medida del ángulo = 120°
Por lo tanto, la medida de cada uno de los ángulos internos del hexágono regular es de 120°.
En resumen, para calcular la medida de un ángulo interno, se utiliza la fórmula 180° – Medida de los ángulos externos. Esta fórmula es útil para cualquier polígono, siempre y cuando se conozca la medida de los ángulos externos.
3. Cálculo de la suma de los ángulos internos
En geometría, la suma de los ángulos internos de un polígono es un concepto fundamental. Para calcular esta suma, se aplica una fórmula específica dependiendo del tipo de polígono.
Polígonos regulares
Un polígono regular es aquel que tiene todos sus ángulos y lados iguales. Para calcular la suma de sus ángulos internos, se utiliza la siguiente fórmula:
Suma de ángulos internos = (n – 2) * 180 grados
Donde n representa el número de lados del polígono.
Polígonos irregulares
En el caso de los polígonos irregulares, es decir, aquellos que tienen lados y ángulos de diferentes medidas, la fórmula para calcular la suma de sus ángulos internos es un poco más compleja.
Se puede calcular la suma utilizando la expresión:
Suma de ángulos internos = (n – 2) * 180 grados
donde n es el número de lados del polígono.
Es importante recordar que la suma de los ángulos internos de cualquier polígono siempre será un número fijo y constante, independientemente de las medidas de sus lados y ángulos. Esta propiedad es muy útil en geometría para resolver problemas y demostrar teoremas.
4. Aplicación práctica del cálculo
A lo largo de la historia, el cálculo ha demostrado ser una herramienta fundamental en diversas áreas de aplicación. Su aplicación práctica se puede observar en diferentes campos, desde la física y la ingeniería hasta la economía y la medicina.
Física
En la física, el cálculo es esencial para el estudio del movimiento y la dinámica de los objetos. Permite calcular la velocidad, la aceleración y la trayectoria de un objeto en movimiento, lo cual es fundamental para comprender fenómenos como el movimiento de los planetas o el lanzamiento de un proyectil.
Ingeniería
En el ámbito de la ingeniería, el cálculo se utiliza para el diseño y la optimización de estructuras y sistemas. Permite analizar cómo diferentes variables afectan el funcionamiento de una máquina o un proceso, y cómo se pueden realizar mejoras para obtener resultados más eficientes o seguros.
Economía
En economía, el cálculo es esencial para el análisis y la modelización de variables como la oferta y la demanda, los costos y los beneficios. Permite realizar proyecciones y tomar decisiones fundamentadas en base a datos numéricos, lo cual es crucial en la toma de decisiones empresariales o en la elaboración de políticas económicas.
Medicina
En medicina, el cálculo tiene aplicaciones en el análisis de datos clínicos, la modelización de fenómenos biológicos y la elaboración de dosis de medicamentos. Permite calcular la dosis adecuada de un medicamento para un paciente en base a diferentes factores, como el peso o la edad, lo cual es vital para garantizar un tratamiento efectivo y seguro.
Estos son solo algunos ejemplos de las aplicaciones prácticas del cálculo en diferentes campos. Su importancia radica en su capacidad para analizar y predecir el comportamiento de variables en situaciones complejas, lo cual es fundamental para la toma de decisiones informadas y el avance en diversas áreas del conocimiento humano.
5. Conclusiones
En conclusión, podemos destacar las siguientes ideas principales:
- Análisis detallado de los datos: Realizar un análisis exhaustivo de los datos recopilados es fundamental para obtener conclusiones sólidas.
- Importancia de la interpretación: No basta con recolectar datos, también es crucial interpretarlos de manera adecuada para extraer información relevante.
- Uso de etiquetas HTML: Utilizar etiquetas HTML adecuadas, como <h3> y <b>, ayuda a dar formato y resaltar información importante en un texto.
- Listas en HTML: Las listas HTML, como <ol> y <ul>, permiten organizar de manera estructurada y jerárquica las ideas presentadas en el texto.
En resumen, es fundamental realizar un análisis detallado de los datos, interpretarlos adecuadamente y utilizar etiquetas HTML y listas para mejorar la presentación y comprensión del contenido.