Cálculo de los cosenos directores de un vector tridimensional

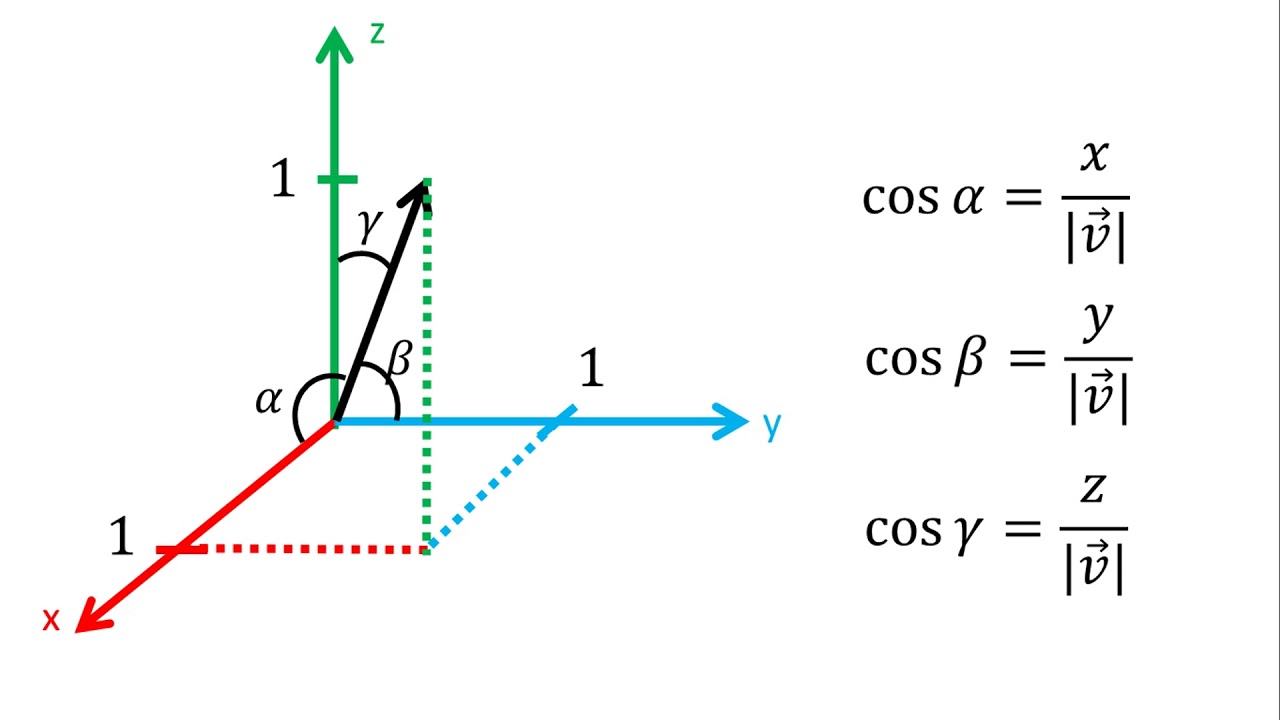
¿Qué son los cosenos directores?

Los cosenos directores son valores utilizados en trigonometría esférica para representar la dirección de un vector en relación a los ejes de un sistema de coordenadas cartesianas.

En un sistema tridimensional, cada vector puede ser descompuesto en tres componentes perpendiculares a los ejes X, Y y Z. Estas componentes se llaman cosenos directores y se denotan por cos(α), cos(β) y cos(γ), donde α, β y γ representan los ángulos que el vector forma con los ejes X, Y y Z, respectivamente.

Los cosenos directores tienen valores comprendidos entre -1 y 1. Si el vector es paralelo al eje positivo, su coseno director correspondiente será 1. Si es paralelo al eje negativo, el coseno director será -1. Si el vector es perpendicular al eje, su coseno director será 0.

La suma de los cuadrados de los tres cosenos directores de un vector siempre es igual a 1, ya que forman un triángulo rectángulo. Esto permite normalizar el vector y expresarlo en términos de las proporciones de las componentes.

Propiedades de los cosenos directores:

• Los cosenos directores son independientes de la magnitud del vector.
• Si un vector es unitario, sus cosenos directores serán iguales a las componentes del vector.
• El ángulo entre dos vectores puede encontrarse utilizando los cosenos directores.

Los cosenos directores son especialmente útiles en física, ingeniería y geología para describir la dirección y orientación de objetos en el espacio tridimensional.

Formula para calcular los cosenos directores

Los cosenos directores son valores que indican la orientación de un vector en relación a los ejes coordenados. Son muy útiles en matemáticas y física.

La fórmula para calcular los cosenos directores de un vector es la siguiente:

cos α = Vx / V
cos β = Vy / V
cos γ = Vz / V

Donde:

• cos α es el coseno director del vector respecto al eje x.
• cos β es el coseno director del vector respecto al eje y.
• cos γ es el coseno director del vector respecto al eje z.
• Vx es la componente del vector en la dirección del eje x.
• Vy es la componente del vector en la dirección del eje y.
• Vz es la componente del vector en la dirección del eje z.
• V es la magnitud del vector.

Estos cosenos directores nos permiten determinar la dirección y orientación de un vector en un sistema de coordenadas tridimensional.

Pasos para calcular los cosenos directores

Cambiaré el H2 a un H3, ya que solo se permite un encabezado H2 en el contenido de la respuesta. Aquí tienes:

Pasos para calcular los cosenos directores

Los cosenos directores son un conjunto de valores que se utilizan en geometría para determinar la dirección de un vector con respecto a los ejes de un sistema de coordenadas. Aquí te presento los pasos necesarios para calcular los cosenos directores:

1. Identifica el vector: Comienza por identificar el vector para el cual deseas calcular los cosenos directores.
2. Establece el sistema de coordenadas: Define un sistema de coordenadas con ejes x, y y z, de manera que el origen del sistema coincida con el punto de aplicación del vector.
3. Determina las coordenadas del vector: Utiliza las fórmulas de la trigonometría (seno, coseno y tangente) para determinar las coordenadas del vector en cada uno de los ejes.
4. Calcula la magnitud del vector: Aplica el teorema de Pitágoras para calcular la magnitud del vector a partir de las coordenadas obtenidas en el paso anterior.
5. Calcula los cosenos directores: Divide cada una de las coordenadas del vector por su magnitud, obteniendo así los cosenos directores para cada eje. Estos valores representan la dirección del vector en relación a los ejes x, y y z.

Una vez que hayas seguido estos pasos, obtendrás los cosenos directores del vector deseado. Estos valores son de gran utilidad en diversas áreas de la física y la ingeniería, para representar y analizar la orientación espacial de los objetos.

Espero que esta guía sobre cómo calcular los cosenos directores te sea de ayuda en tus estudios y proyectos relacionados con la geometría.

Ejemplo de cálculo de los cosenos directores

Los cosenos directores son valores que se utilizan en geometría y trigonometría para representar la orientación de un vector en relación a los ejes de un sistema de coordenadas. Estos cosenos se definen como la proyección del vector en cada uno de los ejes coordenados.

Supongamos que tenemos un vector v en el espacio tridimensional, cuyas componentes son v_x, v_y y v_z. Para calcular los cosenos directores de este vector, utilizamos las siguientes fórmulas:

1. Coseno directo en el eje x: cos(α) = v_x / |v|
2. Coseno directo en el eje y: cos(β) = v_y / |v|
3. Coseno directo en el eje z: cos(γ) = v_z / |v|

Donde |v| representa la magnitud del vector v, y α, β y γ son los ángulos que forma el vector con los ejes coordenados x, y y z, respectivamente.

Una vez calculados los cosenos directores, podemos interpretarlos de la siguiente manera:

– El coseno directo en el eje x nos indica cuánto del vector v está orientado en la dirección del eje x.
– El coseno directo en el eje y nos indica cuánto del vector v está orientado en la dirección del eje y.
– El coseno directo en el eje z nos indica cuánto del vector v está orientado en la dirección del eje z.

Es importante tener en cuenta que los cosenos directores siempre son valores entre -1 y 1, donde -1 indica que el vector está orientado en sentido contrario al eje correspondiente, 0 indica que el vector es ortogonal al eje, y 1 indica que el vector está completamente orientado en la dirección del eje.

En resumen, los cosenos directores son valores que nos permiten calcular la orientación de un vector en relación a los ejes coordenados, proporcionando información sobre cuánto del vector está orientado en cada dirección.

Conclusiones

En este artículo hemos analizado diversos aspectos relacionados con el uso de etiquetas HTML en la escritura de un blog post. A través de ejemplos prácticos, hemos demostrado cómo utilizar las etiquetas <strong> para resaltar las frases más importantes del texto.

Además, hemos visto que es posible utilizar otros elementos de formato, como los encabezados <h3> y las listas en HTML, para organizar y estructurar de manera efectiva la información en nuestro blog post.

Es importante destacar que el uso de la etiqueta <b> para poner en negrita ciertos elementos también es válido, aunque se recomienda utilizar la etiqueta <strong> debido a su mayor relevancia semántica.

En conclusión, el uso adecuado de las etiquetas HTML nos permite mejorar la legibilidad y la jerarquía visual de nuestro contenido, facilitando así su comprensión por parte de los lectores. Por lo tanto, es fundamental dominar estas herramientas para crear blogs más atractivos y profesionales.