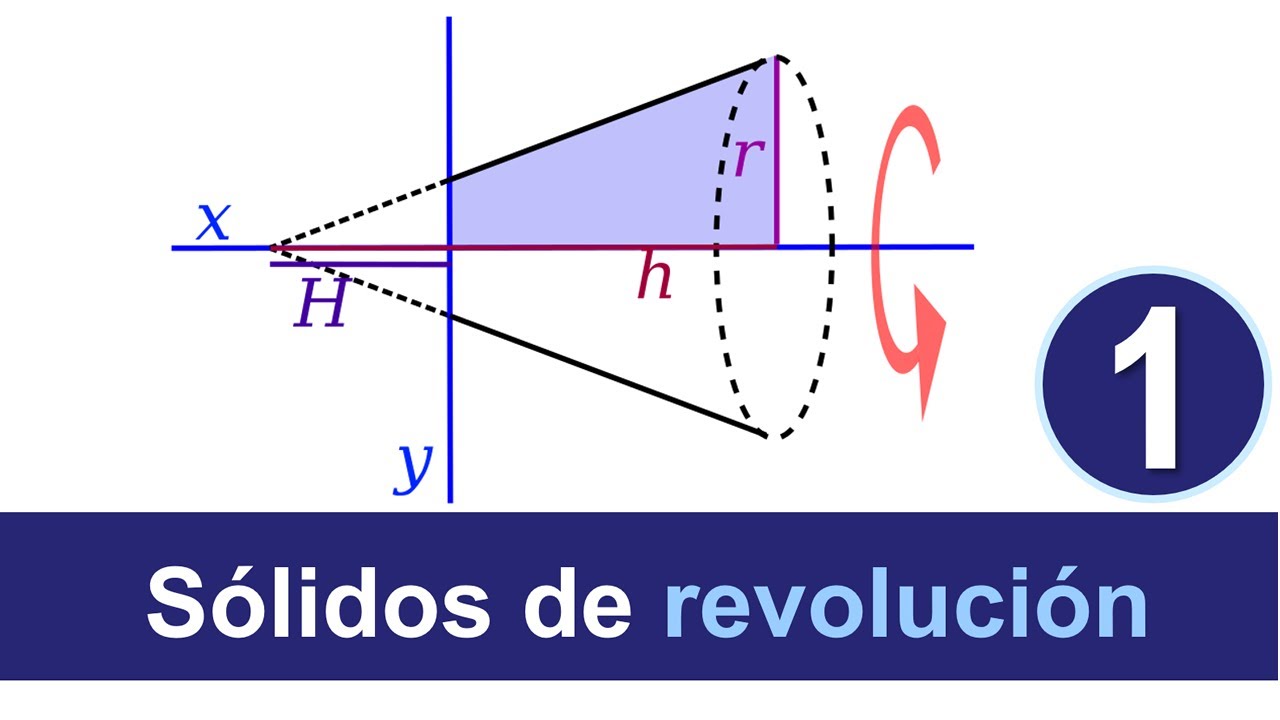
Calcular volúmenes de sólidos mediante revolución es un concepto fundamental en el cálculo y la geometría. Mediante este método, es posible determinar el volumen de sólidos tridimensionales generados al rotar una región bidimensional alrededor de un eje. Este proceso es especialmente útil en la física, la ingeniería y diversas aplicaciones matemáticas.
El método de discos y anillos
El cálculo de volúmenes de sólidos mediante revolución se basa en el método de discos y anillos. Este método es esencial para comprender cómo encontrar el volumen de un sólido generado al hacer girar una región del plano alrededor de un eje. Aprovechando conceptos de integrales y geometría, este enfoque proporciona una forma precisa de determinar volúmenes en situaciones tridimensionales.
Definición de discos y anillos
Para aplicar el método de discos y anillos, es crucial entender la diferencia entre discos y anillos. Un disco se forma al hacer girar una región plana alrededor de un eje, mientras que un anillo se genera al hacer lo mismo con una región anular. Comprender estas formas es fundamental para visualizar y calcular correctamente los volúmenes de los sólidos resultantes.
Concepto de secciones transversales
Otro enfoque clave para el cálculo de volúmenes de sólidos mediante revolución es el concepto de secciones transversales. Al analizar una región bidimensional y su rotación alrededor de un eje, es útil considerar las secciones transversales resultantes en el sólido tridimensional. Estas secciones proporcionan información crucial para determinar el volumen total del sólido.
Relación con integrales
El concepto de secciones transversales está estrechamente relacionado con el uso de integrales para calcular volúmenes. Al descomponer el sólido en secciones transversales y sumar las contribuciones de cada sección, es posible establecer una conexión directa con el cálculo integral. Este enfoque ofrece una poderosa herramienta para encontrar volúmenes de sólidos complejos mediante revolución.
Principales pasos para el cálculo de volúmenes de sólidos
Para calcular el volumen de un sólido generado por la revolución de una región bidimensional, se pueden seguir los siguientes pasos:
Paso 1: Identificar la región a rotar
El primer paso es identificar la región en el plano que se va a rotar alrededor de un eje para formar el sólido tridimensional. Esta región puede ser cualquier forma, desde un simple círculo hasta una región más compleja definida por funciones.
Paso 2: Establecer el eje de rotación
Es crucial determinar el eje alrededor del cual se va a rotar la región. Este eje puede ser horizontal o vertical, y su ubicación afectará la configuración de las secciones transversales y, por lo tanto, el cálculo del volumen.
Paso 3: Definir el espesor de las secciones transversales
El siguiente paso es establecer el grosor o espesor de las secciones transversales. Este valor puede variar a lo largo del eje de rotación y debe considerarse al calcular el volumen total del sólido.
Paso 4: Calcular el área de cada sección transversal
Una vez definido el espesor de las secciones transversales, es posible calcular el área de cada sección. Este paso implica utilizar conceptos de geometría y cálculo para determinar el área de la región transversal resultante de la rotación de la región original.
Paso 5: Aplicar la integral para sumar las contribuciones de todas las secciones
El paso final consiste en utilizar el cálculo integral para sumar las contribuciones de todas las secciones transversales a lo largo del eje de rotación. Esta suma proporcionará el volumen total del sólido generado por revolución.
Ejemplos de aplicación
Para comprender mejor el cálculo de volúmenes de sólidos mediante revolución, es útil explorar algunos ejemplos aplicados. Mediante situaciones prácticas y visualizaciones, es posible entender cómo aplicar de manera efectiva los conceptos y pasos mencionados.
Ejemplo 1: Volumen de un sólido generado por revolución de un círculo
Supongamos que queremos calcular el volumen de un sólido generado al girar un círculo de radio «r» alrededor de un eje que pasa por su centro. Aplicando el método de discos, podemos seguir los pasos mencionados para determinar el volumen de este sólido de forma sencilla y precisa.
Ejemplo 2: Volumen de un sólido generado por revolución de una región definida por una función
En este caso, consideremos una región definida por la función y=f(x) en un intervalo [a, b], y queremos encontrar el volumen del sólido generado al hacer girar esta región alrededor de un eje. Este ejemplo demuestra la versatilidad del método de cálculo de volúmenes de sólidos mediante revolución al aplicarse a situaciones más complejas.
Aplicaciones en la vida real
El cálculo de volúmenes de sólidos mediante revolución tiene diversas aplicaciones en la vida real, especialmente en campos como la física, la ingeniería y la arquitectura. Algunos ejemplos de aplicación incluyen el diseño de piezas mecanizadas, la determinación de volúmenes de fluidos en recipientes y la modelización de objetos tridimensionales en entornos virtuales.
Ingeniería y diseño
En el ámbito de la ingeniería y el diseño, el cálculo de volúmenes de sólidos mediante revolución es fundamental para modelar componentes mecánicos, como rotores, engranajes y componentes de maquinaria. Esta capacidad de determinar volúmenes permite optimizar diseños y prever el comportamiento de piezas en situaciones reales.
Física y dinámica de fluidos
En la física y la dinámica de fluidos, el cálculo de volúmenes de sólidos es crucial para determinar el desplazamiento de fluidos y la capacidad de contenedores. Este enfoque se utiliza para analizar el comportamiento de fluidos en sistemas hidráulicos, recipientes de almacenamiento y tuberías, proporcionando información vital para el diseño y la operación de estos sistemas.
En resumen, el cálculo de volúmenes de sólidos mediante revolución es una herramienta poderosa que tiene aplicaciones sustanciales en varios campos de la ciencia y la ingeniería. Mediante el empleo de conceptos como discos y anillos, secciones transversales e integrales, es posible determinar con precisión el volumen de sólidos tridimensionales generados por la rotación de regiones del plano. Este enfoque ofrece una forma elegante de abordar problemas de volumen en situaciones complejas, y su comprensión es invaluable para aquellos que buscan comprender y aplicar conceptos matemáticos en contextos prácticos.