Calcular el área bajo la curva es un concepto fundamental en el campo del cálculo y la matemática aplicada. Existen varios métodos para realizar este cálculo, entre ellos el uso de extremos derechos e izquierdos. En este artículo, exploraremos en detalle cómo utilizar estos extremos para calcular el área bajo una curva.
La importancia de los extremos en el cálculo del área
Al calcular el área bajo una curva, es crucial entender el papel que juegan los extremos derechos e izquierdos en el proceso. Estos extremos nos permiten aproximar el área utilizando rectángulos, lo que a su vez nos brinda una estimación del área total bajo la curva. El uso de extremos derechos e izquierdos es fundamental en numerosas aplicaciones, tanto en la resolución de problemas matemáticos como en la modelización de fenómenos del mundo real.
Entendiendo el concepto de extremos derechos e izquierdos
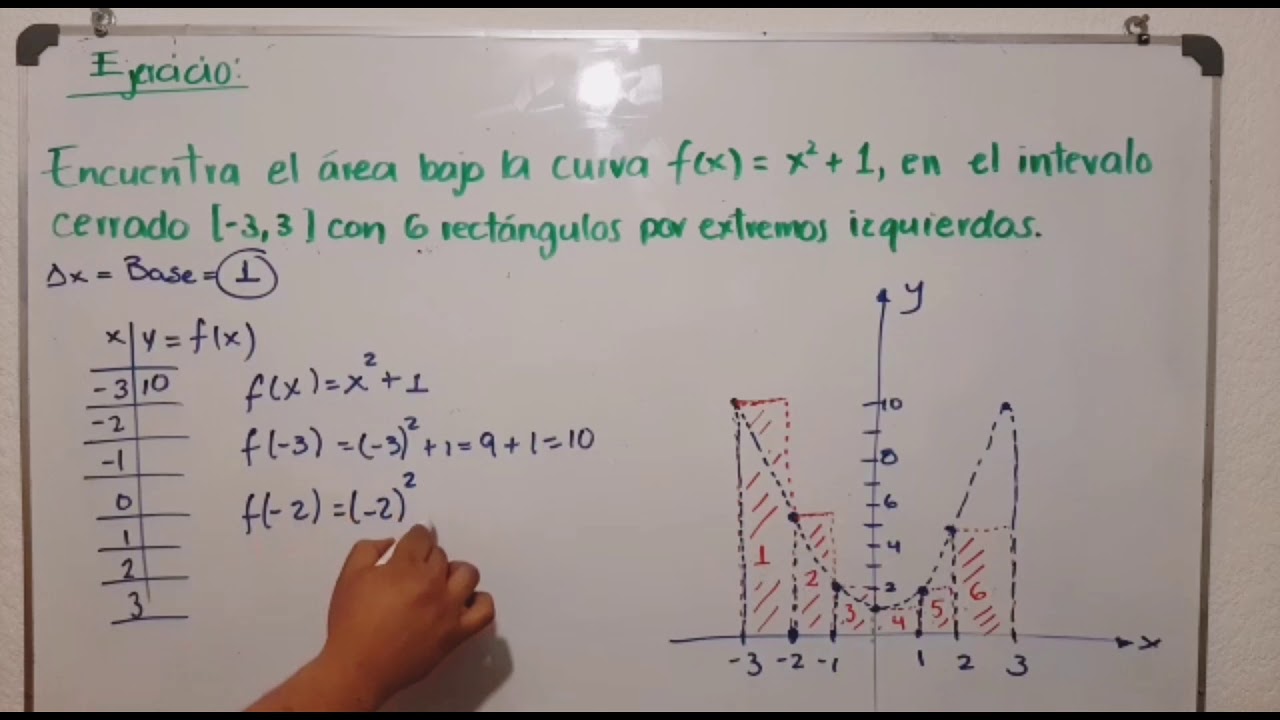
Los extremos derechos e izquierdos se refieren a la forma en que se eligen los puntos para definir los límites de los rectángulos que aproximarán el área bajo la curva. En el caso de los extremos derechos, se utiliza el valor de la función en el extremo derecho de cada subintervalo para definir la altura del rectángulo. Por otro lado, en el caso de los extremos izquierdos, se utiliza el valor de la función en el extremo izquierdo de cada subintervalo.
Algoritmo para calcular el área utilizando extremos derechos e izquierdos
El proceso para calcular el área bajo la curva mediante extremos derechos e izquierdos implica dividir el dominio de la función en subintervalos, calcular la altura de los rectángulos utilizando los valores de la función en los extremos correspondientes, y sumar el área de dichos rectángulos para obtener una estimación del área total. A continuación, detallaremos el algoritmo paso a paso.
Paso 1: Dividir el dominio en subintervalos
El primer paso consiste en dividir el dominio de la función en subintervalos de igual longitud. Esta partición del dominio nos permitirá aproximar el área bajo la curva utilizando rectángulos. Mientras más subintervalos utilicemos, mayor será la precisión de nuestra estimación del área.
Paso 2: Calcular la altura de los rectángulos para los extremos derechos
Una vez que hemos dividido el dominio en subintervalos, procedemos a calcular la altura de los rectángulos para los extremos derechos. Para cada subintervalo, tomamos el valor de la función en el extremo derecho del subintervalo y lo utilizamos como la altura del rectángulo correspondiente.
Paso 3: Calcular la altura de los rectángulos para los extremos izquierdos
De manera similar, también calculamos la altura de los rectángulos para los extremos izquierdos. En este caso, utilizamos el valor de la función en el extremo izquierdo de cada subintervalo como la altura del rectángulo correspondiente.
Paso 4: Sumar el área de los rectángulos
Una vez que hemos calculado la altura de los rectángulos para los extremos derechos e izquierdos, sumamos el área de dichos rectángulos para obtener una estimación del área total bajo la curva. Esta suma nos brindará una aproximación del área que queremos calcular.
Ventajas y desventajas del método de extremos derechos e izquierdos
Si bien el método de extremos derechos e izquierdos es útil para aproximar el área bajo una curva, tiene sus ventajas y desventajas. Por un lado, este método es relativamente sencillo de entender e implementar, lo que lo hace accesible para estudiantes y profesionales. Además, proporciona una estimación razonable del área sin requerir un cálculo complejo.
Por otro lado, el método de extremos derechos e izquierdos puede subestimar o sobrestimar el área real bajo la curva, especialmente en casos donde la función presenta variaciones significativas en cortos intervalos. Además, la precisión de la estimación dependerá de la cantidad de subintervalos utilizados, lo que puede requerir un esfuerzo adicional para obtener una aproximación más precisa del área.
Aplicaciones del cálculo del área bajo la curva
El cálculo del área bajo la curva mediante extremos derechos e izquierdos tiene numerosas aplicaciones en diferentes campos. En matemáticas, este concepto es fundamental en la teoría de la integración y el cálculo de áreas de regiones no delimitadas por funciones lineales. En ciencias de la computación, el cálculo del área bajo la curva se utiliza en la resolución de problemas de optimización y modelado matemático de fenómenos naturales. Asimismo, en la ingeniería y la física, el cálculo del área bajo la curva es esencial en el análisis de fenómenos físicos y en la modelización de sistemas dinámicos.
Conclusiones
El cálculo del área bajo la curva mediante extremos derechos e izquierdos es un tema apasionante que combina conceptos fundamentales del cálculo con aplicaciones prácticas en diversas disciplinas. A través de la comprensión de los extremos y el proceso de aproximación del área, podemos estimar de manera efectiva el área bajo una curva y aplicar este conocimiento en situaciones del mundo real. Si bien el método de extremos derechos e izquierdos tiene sus limitaciones, su utilidad y relevancia en la resolución de problemas matemáticos y científicos lo convierten en una herramienta valiosa para estudiantes, investigadores y profesionales.