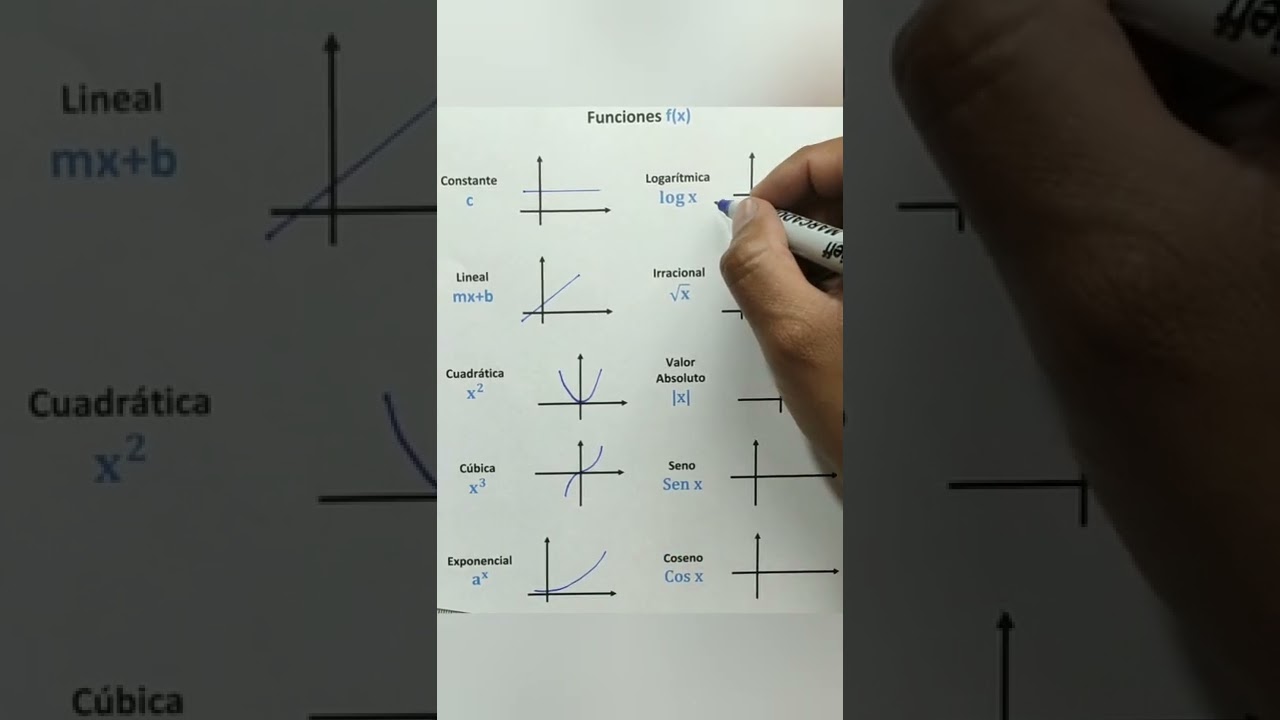
1. Funciones lineales
Llamamos función lineal a aquella que tiene una forma de ecuación y = mx + b. En esta ecuación, m representa la pendiente de la recta y b es la ordenada al origen.
La pendiente de una función lineal determina la dirección y la inclinación de la recta en el plano cartesiano. Si la pendiente es positiva, la recta sube hacia la derecha, mientras que si es negativa, la recta baja hacia la derecha.
La ordenada al origen indica el punto en el que la recta intersecta el eje vertical, es decir, cuando x = 0. Si la ordenada al origen es positiva, la recta cortará al eje Y por encima del origen, y si es negativa, la cortará por debajo del origen.
Ejemplo de función lineal:
Tomemos la ecuación y = 2x + 3. En este caso, la pendiente es 2 y la ordenada al origen es 3. Esto quiere decir que la recta subirá 2 unidades en el eje Y por cada unidad que se desplace hacia la derecha en el eje X. Además, esta recta intersectará el eje Y en el punto (0, 3).
Al representar la función lineal en un gráfico, obtendremos una recta que seguirá estas características. Podemos determinar puntos adicionales en la recta al asignar valores a x y calcular el correspondiente y.
En resumen, las funciones lineales son aquellas que siguen una ecuación de la forma y = mx + b, donde m es la pendiente y b la ordenada al origen. Estas funciones se representan por medio de rectas en el plano cartesiano.
2. Funciones no lineales
En matemáticas, una función no lineal es aquella que no sigue una relación directa de proporcionalidad entre las variables involucradas. A diferencia de las funciones lineales, que se representan mediante una línea recta, las funciones no lineales tienen expresiones más complejas y pueden tener formas curvas en su gráfica.
Estas funciones son muy comunes en diversos campos de estudio, como la física, la economía y la biología, ya que representan situaciones y fenómenos más realistas y no limitados a relaciones lineales simples.
Una forma común de representar una función no lineal es mediante una ecuación de la forma y = f(x), donde f(x) es una expresión matemática que describe cómo se relacionan las variables x e y. Esta expresión puede ser polinómica, exponencial, logarítmica, trigonométrica, entre otras.
Algunos ejemplos de funciones no lineales incluyen:
- Función cuadrática: $y = ax^2 + bx + c$, donde $a$, $b$ y $c$ son constantes.
- Función exponencial: $y = a cdot e^{bx}$, donde $a$ y $b$ son constantes y $e$ es la base del logaritmo natural.
- Función trigonométrica: $y = a cdot sin(bx)$ o $y = a cdot cos(bx)$, donde $a$ y $b$ son constantes.
Es importante tener en cuenta que las funciones no lineales pueden tener comportamientos y propiedades únicos, como puntos de inflexión, asíntotas, períodos o amplitudes. Además, su análisis y resolución puede requerir métodos más avanzados, como el cálculo diferencial e integral.
En resumen, las funciones no lineales son aquellas que no siguen una relación proporcional simple entre las variables. Son utilizadas para modelar una amplia variedad de fenómenos y situaciones, y su estudio puede ser más complejo que el de las funciones lineales.
3. Ejemplos de funciones lineales
Una función lineal es una función matemática que se define como f(x) = mx + b, donde m es la pendiente de la recta y b es la ordenada al origen.
A continuación, se presentan tres ejemplos de funciones lineales:
Ejemplo 1:
Sea la función f(x) = 2x + 3. En este caso, la pendiente es 2 y la ordenada al origen es 3. Esto significa que por cada unidad que incremente el valor de x, el valor de y se incrementará en 2.
Ejemplo 2:
Consideremos la función f(x) = -0.5x + 4. La pendiente en este caso es -0.5 y la ordenada al origen es 4. Esto implica que por cada unidad que aumente el valor de x, el valor de y disminuirá en 0.5.
Ejemplo 3:
Tomemos la función f(x) = 3x. Aquí, la pendiente es 3 y la ordenada al origen es 0, ya que no hay una constante adicional. Esto significa que por cada unidad que se incremente la variable x, el valor de y se incrementará en 3.
Estos ejemplos ilustran cómo las funciones lineales se representan mediante una ecuación de la forma f(x) = mx + b, donde la pendiente y la ordenada al origen determinan la relación entre las variables x e y.
4. Ejemplos de funciones no lineales
A continuación, mencionaremos algunos ejemplos de funciones no lineales:
1. Función cuadrática:
La función cuadrática es una de las funciones no lineales más comunes. Se representa como f(x) = ax^2 + bx + c, donde a, b y c son constantes y a ≠ 0. Esta función tiene la forma de una parábola y su gráfica no es una línea recta. Un ejemplo de una función cuadrática es f(x) = 2x^2 – 3x + 1.
2. Función exponencial:
La función exponencial se representa como f(x) = a^x, donde a es una constante y x es el exponente. Esta función tiene la característica de crecer o decrecer de manera rápida. Un ejemplo de una función exponencial es f(x) = 2^x.
3. Función trigonométrica:
Las funciones trigonométricas, como la función seno y la función coseno, son ejemplos de funciones no lineales. Estas funciones tienen un comportamiento periódico y su gráfica no es una línea recta. Un ejemplo de una función trigonométrica es la función seno, representada como f(x) = sin(x).
4. Función logarítmica:
La función logarítmica se representa como f(x) = log(x) o f(x) = ln(x), donde x es el argumento del logaritmo. Esta función tiene una gráfica curva y no lineal. Un ejemplo de una función logarítmica es f(x) = log(x).
Estos son solo algunos ejemplos de funciones no lineales, y existen muchas más. Estas funciones son importantes y se utilizan en diversos campos de las matemáticas y la ciencia para modelar fenómenos complejos que no siguen una relación directamente proporcional.
5. Importancia de la clasificación de funciones
La clasificación de funciones es una herramienta fundamental en diferentes áreas, ya que permite organizar y categorizar las tareas y responsabilidades dentro de una organización o sistema.
1. Optimización de recursos: La clasificación de funciones permite asignar de manera eficiente los recursos humanos y materiales, evitando la duplicación de tareas y optimizando el uso de los mismos.
2. Mejora de la comunicación: Al tener funciones claramente definidas y categorizadas, se facilita la comunicación entre los miembros de un equipo de trabajo. Cada persona sabe cuáles son sus responsabilidades y a quién debe dirigirse para coordinar o solicitar información.
3. Identificación de habilidades y talentos: Al clasificar las funciones, se hace evidente cuáles son las habilidades necesarias para cada tarea. Esto permite identificar los talentos dentro del equipo y asignar a cada persona a las tareas en las que es más competente.
4. Evaluación del desempeño: La clasificación de funciones facilita la evaluación del desempeño de los miembros de un equipo. Al tener tareas y responsabilidades claramente definidas, se puede medir de manera objetiva el cumplimiento de objetivos y metas.
5. Eficiencia y efectividad: La clasificación de funciones contribuye a la eficiencia y efectividad de una organización. Al tener roles y responsabilidades bien definidos, se evita la superposición de tareas y se promueve un trabajo más organizado y productivo.
En conclusión, la clasificación de funciones es de vital importancia para una organización. Contribuye a la optimización de recursos, mejora la comunicación, identifica habilidades y talentos, facilita la evaluación del desempeño y promueve la eficiencia y efectividad. Es una herramienta que permite un trabajo más organizado y productivo.