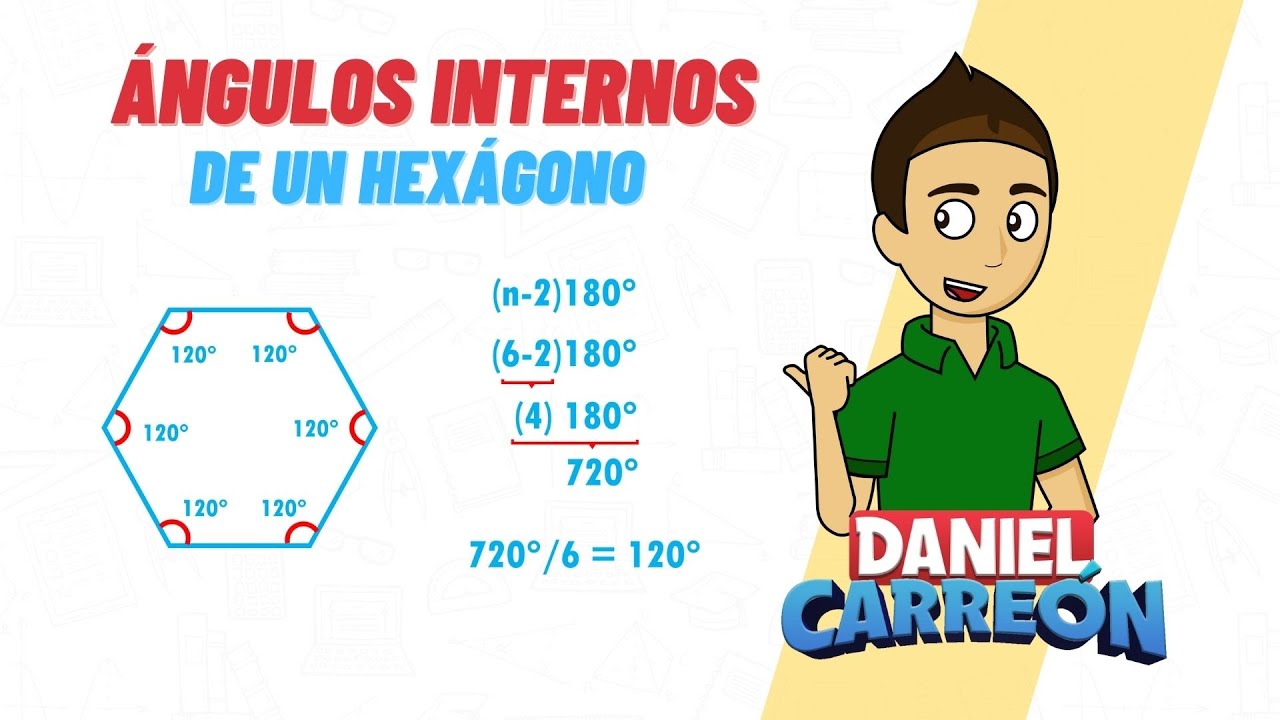
¿Qué es un hexágono?
Un hexágono es una figura geométrica de seis lados y seis ángulos. Es uno de los polígonos más comunes y reconocibles.
El término “hexágono” proviene de la combinación de las palabras griegas “hexa”, que significa “seis”, y “gonia”, que se traduce como “ángulo”. Por lo tanto, un hexágono se define como un polígono de seis ángulos.
Características de un hexágono:
- Tiene seis lados y seis ángulos.
- Todos sus ángulos internos suman 720 grados.
- Todas sus líneas diagonales son iguales en longitud.
- Es un polígono regular si todos sus lados y ángulos son iguales.
Propiedades de un hexágono regular:
- Todos sus lados tienen la misma longitud.
- Todos sus ángulos internos miden 120 grados.
- Tiene simetría de rotación de 60 grados.
- Puede ser inscrito dentro de un círculo, con todos sus vértices tocando la circunferencia.
Los hexágonos son ampliamente utilizados en diversas áreas, como la arquitectura, la biología, la geología, la física y las matemáticas. Por ejemplo, en la geometría molecular, la estructura de un cristal o la forma de una colmena de abejas son ejemplos de hexágonos en la naturaleza.
En conclusión, un hexágono es un polígono de seis lados y seis ángulos. Su forma regular y sus características geométricas lo hacen una figura interesante y versatile en diversas disciplinas.
Fórmula para calcular el ángulo interior de un hexágono regular
El ángulo interior de un hexágono regular se puede calcular utilizando la siguiente fórmula:
Ángulo interior = (6 – 2) * 180° / 6
Donde:
- 6 es el número de lados del hexágono.
- 2 es el número de diagonales por vértice.
- 180° es la medida de un ángulo recto.
Al simplificar la fórmula, nos queda:
Ángulo interior = 120°
Esto significa que todos los ángulos interiores de un hexágono regular tienen una medida de 120°.
Es importante destacar que esta fórmula aplica únicamente a hexágonos regulares, es decir, aquellos que tienen todos sus lados y ángulos iguales.
Calcular el ángulo interior de un hexágono irregular
Un hexágono irregular es un polígono de seis lados donde cada ángulo interior puede tener diferentes medidas. Para calcular el ángulo interior de un hexágono irregular, necesitamos conocer algunos datos adicionales.
Método 1: Suma de ángulos
Una forma de calcular el ángulo interior de un hexágono irregular es dividiéndolo en triángulos. Podemos trazar diagonales desde un vértice a los otros vértices adyacentes, dividiendo así el hexágono en seis triángulos.
Para obtener el ángulo interior de cada triángulo, podemos utilizar la fórmula de la suma de ángulos de un triángulo, que establece que la suma de los ángulos interiores de un triángulo es siempre igual a 180 grados.
Supongamos que conocemos los ángulos internos de cinco de los triángulos del hexágono irregular. Podemos sumar estos cinco ángulos y luego restarlo de 180 grados para encontrar el ángulo interior faltante.
Método 2: Conocer las medidas de los lados
Otra forma de calcular el ángulo interior de un hexágono irregular es conociendo las medidas de los lados del hexágono. Podemos aplicar el teorema del coseno o el teorema de los senos para calcular los ángulos internos.
El teorema del coseno se utiliza cuando se conocen las medidas de los tres lados de un triángulo y permite calcular uno de los ángulos internos utilizando la ecuación:
c^2 = a^2 + b^2 – 2ab * cos(C)
Donde c es el lado opuesto al ángulo C, y a y b son los otros dos lados del triángulo.
Si conocemos las medidas de los seis lados del hexágono irregular, podemos usar el teorema del coseno en diferentes combinaciones de triángulos para calcular los ángulos internos.
El teorema de los senos se utiliza cuando se conocen dos ángulos y un lado opuesto a uno de ellos, y permite calcular los lados o ángulos desconocidos con la siguiente ecuación:
a/sin(A) = b/sin(B) = c/sin(C)
Donde a, b y c son los lados del triángulo opuestos a los ángulos A, B y C, respectivamente. Usando el teorema de los senos, también podemos calcular los ángulos internos si conocemos las medidas de los lados del hexágono irregular.
Como podemos ver, calcular el ángulo interior de un hexágono irregular puede ser un proceso complejo y requiere de datos adicionales. En resumen, es posible calcular el ángulo interior de un hexágono irregular utilizando métodos como la suma de ángulos o los teoremas del coseno y los senos si conocemos las medidas de los lados o ángulos del hexágono.
Método para calcular el ángulo interior de un hexágono irregular
El cálculo del ángulo interior de un hexágono irregular puede ser un desafío interesante. A diferencia de un hexágono regular, cuyos ángulos interiores son todos iguales a 120 grados, un hexágono irregular puede tener ángulos interiores de diferentes medidas. Aquí te presento un método para calcularlos.
En primer lugar, es importante recordar que la suma de los ángulos interiores de cualquier polígono siempre es igual a la cantidad de lados menos 2 multiplicado por 180 grados. En el caso de un hexágono, que tiene seis lados, la fórmula sería:
Suma de ángulos interiores = (6 – 2) * 180 grados = 4 * 180 grados = 720 grados
Ahora, si conocemos la medida de algunos ángulos interiores del hexágono irregular, podemos utilizar esta fórmula para encontrar el valor del ángulo restante. Por ejemplo, si tenemos cinco ángulos de 135 grados cada uno, podemos sumarlos y restar esa cantidad de 720 grados para encontrar el sexto ángulo:
Suma de ángulos conocidos = 5 * 135 grados = 675 grados
Ángulo restante = 720 grados – 675 grados = 45 grados
Por lo tanto, el ángulo interior restante del hexágono irregular sería de 45 grados en este caso.
Es importante mencionar que este método solo nos brinda una forma de calcular un ángulo interior en función de los demás ángulos conocidos. Si no tenemos información sobre los demás ángulos, puede resultar más complicado determinar la medida de un ángulo interior específico.
Conclusión
En mi opinión, la inclusión de etiquetas HTML en las frases más importantes del texto es una excelente práctica para resaltar dichos puntos clave. Además, el uso de encabezados H3 proporciona una jerarquía visual clara y estructurada en el contenido.
También es recomendable utilizar listas en HTML, ya que ayudan a organizar la información de manera concisa y fácil de leer. Las listas pueden ser tanto numeradas como no numeradas, dependiendo de la naturaleza del contenido.
Además de las etiquetas HTML mencionadas anteriormente, se puede utilizar la etiqueta para aplicar negritas a palabras o frases específicas dentro del texto. Esto ayuda a llamar la atención del lector hacia información importante o destacada.
En resumen, mediante el uso estratégico de etiquetas HTML como , encabezados H3, listas y negritas (), se puede mejorar la legibilidad y la organización del contenido de un blog post en HTML. Estas herramientas son fundamentales para crear una experiencia de lectura agradable y efectiva para los visitantes del sitio web.