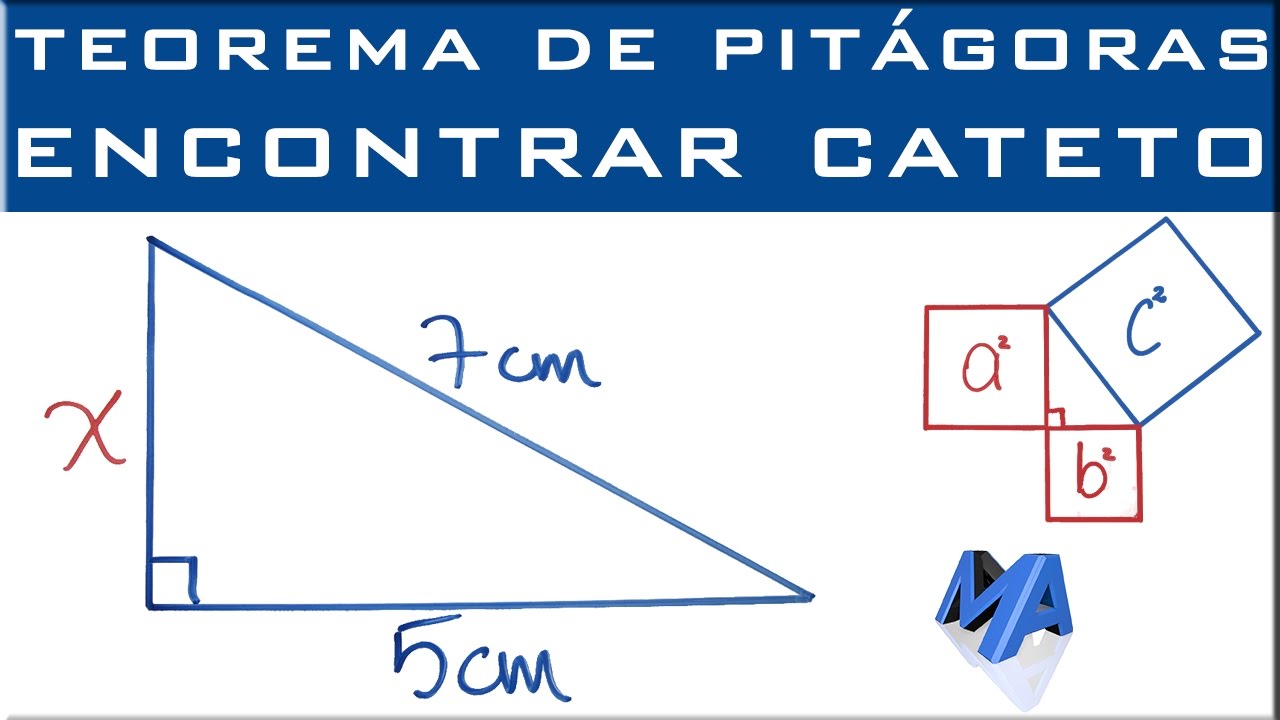
1. ¿Qué es un triángulo rectángulo?
Un triángulo rectángulo es un tipo de triángulo que contiene un ángulo recto, es decir, un ángulo de 90 grados.
Existen algunas características importantes que definen a un triángulo rectángulo:
- Hipotenusa: Es el lado más largo del triángulo rectángulo y se encuentra opuesto al ángulo recto.
- Catetos: Son los dos lados más cortos del triángulo rectángulo y forman el ángulo recto.
Además, el Teorema de Pitágoras se aplica solo a los triángulos rectángulos. Este teorema establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
Es importante destacar que los triángulos rectángulos son muy utilizados en la trigonometría, ya que sus propiedades permiten calcular ratios, como el seno, coseno y tangente de los ángulos agudos.
En resumen, un triángulo rectángulo es aquel que posee un ángulo recto y se caracteriza por la hipotenusa y los catetos. Su importancia radica en la aplicación del Teorema de Pitágoras y de los conceptos trigonométricos.
2. Fórmula básica para calcular el cateto
En la geometría básica, el cateto es uno de los lados que forman un triángulo rectángulo. La fórmula básica para calcular la longitud de un cateto es:
Longitud del cateto = hipotenusa * seno(ángulo agudo)
Para utilizar esta fórmula, necesitamos conocer la longitud de la hipotenusa y el valor del ángulo agudo. La hipotenusa es el lado opuesto al ángulo recto y el ángulo agudo es el ángulo formado por la hipotenusa y el cateto que queremos calcular.
Una forma común de recordar esta fórmula es a través del famoso Teorema de Pitágoras, que establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. A partir de esta fórmula, podemos despejar la longitud de un cateto si conocemos la longitud de la hipotenusa y la longitud del otro cateto.
Por ejemplo, si queremos calcular la longitud de un cateto en un triángulo rectángulo con una hipotenusa de 5 unidades y un ángulo agudo de 30 grados, podemos utilizar la fórmula mencionada anteriormente:
Longitud del cateto = 5 * seno(30)
Para calcular el seno de un ángulo, podemos consultar tablas trigonométricas o utilizar una calculadora científica. En este caso, el seno de 30 grados es aproximadamente 0.5.
Por lo tanto, la longitud del cateto en este ejemplo sería:
Longitud del cateto = 5 * 0.5 = 2.5 unidades
Esta fórmula es muy útil para resolver problemas de geometría que involucran triángulos rectángulos. Así que ya sabes, si necesitas calcular la longitud de un cateto, solo debes recordar esta fórmula básica y utilizarla correctamente. ¡Espero que este artículo te haya sido útil!
3. Método eficiente para calcular el cateto
En esta ocasión, vamos a hablar sobre un método eficiente para calcular el cateto de un triángulo.
Cateto de un triángulo rectángulo
Antes de entrar en detalles sobre el método eficiente, recordemos qué es el cateto en un triángulo rectángulo. Un triángulo rectángulo es aquel que tiene un ángulo recto, es decir, un ángulo de 90 grados. Los catetos son los dos lados que forman el ángulo recto, mientras que la hipotenusa es el lado opuesto al ángulo recto.
Ahora bien, ¿cómo podemos calcular el valor de un cateto? La fórmula para el cálculo del cateto depende de la información que tengamos. Si conocemos la hipotenusa y el otro cateto, podemos utilizar el teorema de Pitágoras. Sin embargo, cuando solo conocemos la hipotenusa y el ángulo formado con el cateto desconocido, necesitamos un método más eficiente.
Método eficiente para calcular el cateto
Este método se basa en el uso de las funciones trigonométricas, específicamente la función seno. Para calcular el cateto desconocido, utilizamos la fórmula:
cateto = hipotenusa * seno(ángulo)
Donde “cateto” representa el valor que queremos calcular, “hipotenusa” es el valor conocido de la hipotenusa y “ángulo” es el valor conocido del ángulo formado con el cateto desconocido.
Veamos un ejemplo práctico. Supongamos que tenemos un triángulo rectángulo con una hipotenusa de 10 unidades y un ángulo de 30 grados con el cateto desconocido. Aplicamos la fórmula:
cateto = 10 * seno(30)
Utilizando una calculadora, podemos obtener el valor del seno de 30 grados, que es aproximadamente 0.5. Por lo tanto, el cateto sería:
cateto = 10 * 0.5 = 5 unidades
¡Y así hemos calculado el valor del cateto utilizando este método eficiente!
Recuerda que este método solo funciona cuando conocemos la hipotenusa y el ángulo formado con el cateto desconocido. Si no tenemos esta información, debemos utilizar otras fórmulas o teoremas para el cálculo del cateto.
Espero que este método eficiente te sea de utilidad en tus cálculos de catetos en triángulos rectángulos. ¡Hasta la próxima!
4. Ejemplo de cálculo de cateto utilizando el seno
En geometría, el teorema de Pitágoras es muy conocido y utilizado para calcular las longitudes de los lados de un triángulo rectángulo. Sin embargo, en algunas ocasiones, no conocemos uno de los catetos y necesitamos calcularlo.
Para ello, podemos utilizar el seno de uno de los ángulos agudos del triángulo rectángulo. El seno de un ángulo se define como la relación entre la longitud del cateto opuesto al ángulo y la hipotenusa del triángulo.
Entonces, si conocemos la medida del ángulo agudo y la longitud de la hipotenusa, podemos calcular la longitud del cateto utilizando la siguiente fórmula:
cateto = sen(ángulo) * hipotenusa
Veamos un ejemplo:
Ejemplo:
Tenemos un triángulo rectángulo en el que la hipotenusa mide 5 unidades y el ángulo agudo es de 30 grados.
Para calcular la longitud del cateto, utilizamos la fórmula:
cateto = sen(30 grados) * 5 unidades
El seno de 30 grados es igual a 0.5, por lo tanto:
cateto = 0.5 * 5 = 2.5 unidades
Entonces, el cateto tiene una longitud de 2.5 unidades.
Este es solo un ejemplo de cómo utilizar el seno para calcular la longitud de un cateto en un triángulo rectángulo. Dependiendo del conocimiento que tengamos de los elementos del triángulo, podemos utilizar otras fórmulas y relaciones trigonométricas.
5. Otros métodos para calcular el cateto
El cateto es uno de los elementos más importantes en el cálculo de triángulos rectángulos. Además de la fórmula clásica que utiliza el teorema de Pitágoras, existen otros métodos que también pueden utilizarse para calcular el cateto de un triángulo rectángulo.
Método del ángulo complementario:
Este método se basa en utilizar la relación entre los ángulos complementarios de un triángulo rectángulo. Si conocemos uno de los ángulos agudos y el valor de la hipotenusa, podemos utilizar funciones trigonométricas para calcular el valor del cateto. Por ejemplo, si conocemos el ángulo agudo α y la hipotenusa c, podemos utilizar la función seno para calcular el valor del cateto opuesto, que sería igual a c * sen(α).
Método de la proporcionalidad:
Otro método utilizado para calcular el cateto es el de la proporcionalidad. Si conocemos el valor de uno de los catetos y la relación entre los catetos del triángulo (por ejemplo, si sabemos que uno de los catetos es el doble del otro), podemos utilizar reglas de proporcionalidad para calcular el valor del otro cateto. Por ejemplo, si conocemos que el cateto opuesto es el doble del cateto adyacente (x = 2y), podemos utilizar esta ecuación para calcular el valor de x.
Método del cateto adyacente:
En algunos casos, también podemos utilizar la relación entre los catetos de un triángulo rectángulo para calcular el valor de uno de los catetos. Si conocemos el valor de uno de los catetos y el ángulo agudo opuesto, podemos utilizar funciones trigonométricas para calcular el valor del otro cateto. Por ejemplo, si conocemos el cateto adyacente a un ángulo agudo β y el valor de la hipotenusa, podemos utilizar la función coseno para calcular el valor del cateto opuesto, que sería igual a c * cos(β).
Estos son solo algunos métodos alternativos para calcular el cateto de un triángulo rectángulo. Es importante recordar que en todos los casos es necesario tener al menos dos valores conocidos, ya sean los valores de los catetos, el valor de la hipotenusa o el valor de los ángulos agudos.