Cómo calcular el tercer lado utilizando el teorema de Pitágoras

¿Qué es el teorema de Pitágoras y para qué se utiliza?

El teorema de Pitágoras es una de las relaciones matemáticas más fundamentales en geometría, que establece una relación entre los lados de un triángulo rectángulo. Este teorema establece que en todo triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los catetos.

En otras palabras, si a y b son las longitudes de los catetos de un triángulo rectángulo, y c es la longitud de la hipotenusa, el teorema de Pitágoras se expresa matemáticamente como:

c² = a² + b²

Este teorema es ampliamente utilizado en diversos campos como la arquitectura, la ingeniería, la física y la navegación. Al conocer la longitud de dos lados de un triángulo rectángulo, podemos utilizar el teorema de Pitágoras para encontrar la longitud del tercer lado. También es útil para determinar si un triángulo es rectángulo, ya que si la relación de los lados cumple con el teorema, entonces el triángulo es rectángulo.

En resumen, el teorema de Pitágoras es una herramienta fundamental para resolver problemas geométricos relacionados con triángulos rectángulos y se utiliza para encontrar la longitud de lados desconocidos y verificar si un triángulo es rectángulo.

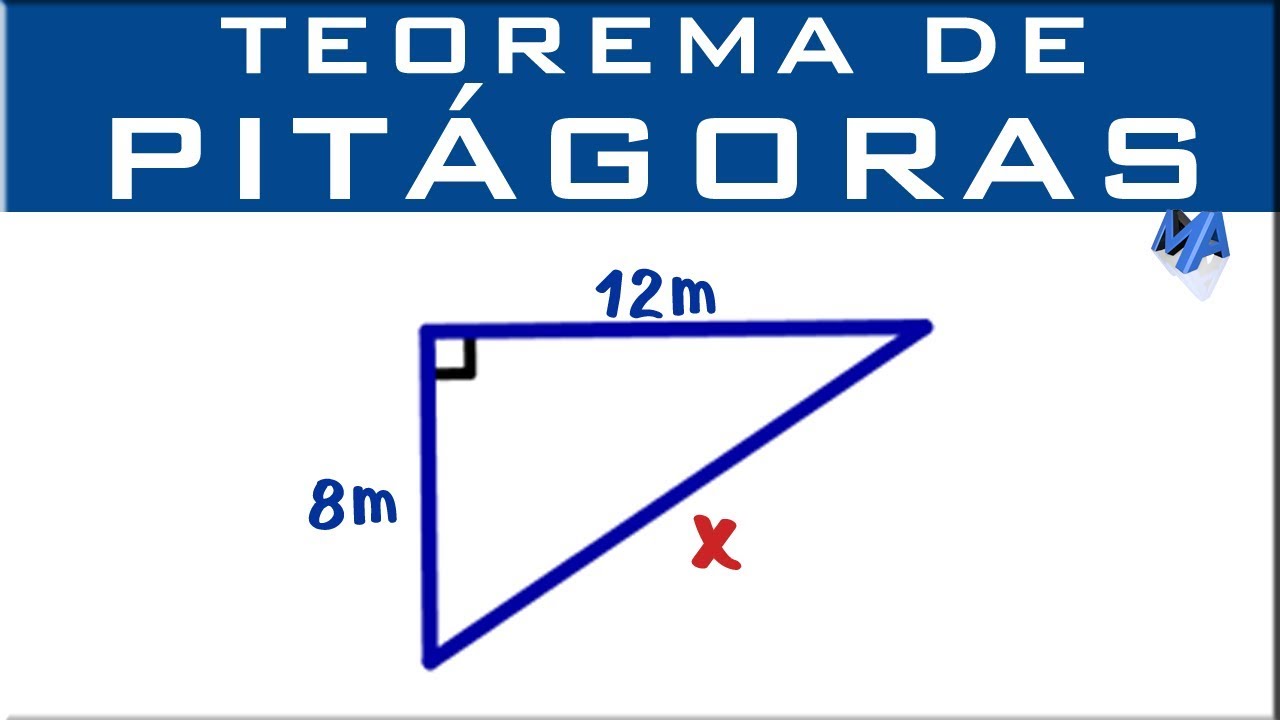
Paso a paso: Cómo calcular el tercer lado con el teorema de Pitágoras

En geometría, el teorema de Pitágoras establece que en un triángulo rectángulo, el cuadrado de la longitud de la hipotenusa es igual a la suma de los cuadrados de las longitudes de los otros dos lados. Este teorema es fundamental para el cálculo de los lados de un triángulo rectángulo cuando se conocen las longitudes de otros dos lados.

Para calcular el tercer lado de un triángulo rectángulo utilizando el teorema de Pitágoras, se deben seguir los siguientes pasos:

1. Identificación de los lados: Se deben identificar cuál de los lados del triángulo es la hipotenusa y cuáles son los otros dos lados.
2. Aplicación del teorema: Se debe aplicar el teorema de Pitágoras, que establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa.
3. Despeje de la incógnita: Se debe despejar la incógnita, que en este caso es la longitud del tercer lado del triángulo rectángulo.
4. Cálculo del tercer lado: Se debe realizar la operación matemática para calcular el valor del tercer lado.

En resumen, para calcular el tercer lado de un triángulo rectángulo se deben identificar los lados, aplicar el teorema de Pitágoras, despejar la incógnita y realizar la operación matemática correspondiente.

Ejemplo práctico: Calcular el tercer lado de un triángulo rectángulo

A veces nos encontramos en situaciones en las que necesitamos calcular el tercer lado de un triángulo rectángulo. Para ello, podemos utilizar el teorema de Pitágoras, que establece que en un triángulo rectángulo el cuadrado de la hipotenusa (el lado más largo) es igual a la suma de los cuadrados de los otros dos lados.

Supongamos que conocemos la longitud de los dos lados que forman el ángulo recto, también conocidos como catetos. Llamémosles “a” y “b”.)

Paso a paso

1. Identificar los valores conocidos: En este caso, los valores conocidos son la longitud de los dos catetos “a” y “b”.
2. Aplicar el teorema de Pitágoras: Conocemos los valores de “a” y “b”, entonces podemos sustituir en la fórmula:
   • a² + b² = c²
3. Resolver la ecuación: Realizamos las operaciones necesarias para encontrar el valor de “c”, que es el tercer lado del triángulo rectángulo.
4. Calcular la raíz cuadrada: Si la ecuación se resuelve correctamente, obtendremos c² = c². Para obtener el valor exacto de “c”, calculamos la raíz cuadrada del resultado.
5. El resultado: Una vez obtenido el valor de “c”, hemos calculado el tercer lado del triángulo rectángulo.

Ahora que sabemos cómo calcular el tercer lado de un triángulo rectángulo, podemos aplicar este ejemplo práctico a situaciones reales. Recuerda siempre verificar que los valores conocidos sean correctos y seguir los pasos cuidadosamente para obtener un resultado preciso.

Consejos útiles: Errores comunes al aplicar el teorema de Pitágoras

El teorema de Pitágoras es una herramienta fundamental en la geometría que nos permite calcular la longitud de un lado de un triángulo rectángulo. Aunque puede parecer sencillo de aplicar, muchos cometen errores comunes que pueden llevar a obtener resultados incorrectos. Aquí te presento algunos consejos útiles para evitar estos errores:

1. No identificar correctamente los lados del triángulo:

Uno de los errores más comunes al aplicar el teorema de Pitágoras es no identificar correctamente cuál es el cateto y cuál es la hipotenusa en el triángulo rectángulo. Recuerda que el teorema establece que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Por lo tanto, es fundamental identificar claramente cuáles son los lados del triángulo para aplicar correctamente la fórmula.

2. No utilizar la fórmula correcta:

Otro error común es utilizar la fórmula incorrecta al aplicar el teorema de Pitágoras. La fórmula correcta es a^2 + b^2 = c^2, donde a y b representan los catetos y c representa la hipotenusa. Asegúrate de utilizar esta fórmula de manera adecuada para evitar obtener resultados incorrectos.

3. No simplificar correctamente las operaciones:

A veces, los errores se deben a no simplificar correctamente las operaciones. Es importante realizar las operaciones matemáticas en el orden correcto y simplificar los valores obtenidos antes de concluir con el cálculo. Esto evitará errores en los resultados finales.

4. No verificar los resultados obtenidos:

Por último, es esencial verificar los resultados obtenidos al aplicar el teorema de Pitágoras. Esto se puede hacer calculando la suma de los cuadrados de los catetos y comparándola con el cuadrado de la hipotenusa. Si ambos resultados coinciden, significa que hemos aplicado correctamente el teorema y hemos obtenido la respuesta correcta.

Siguiendo estos consejos, podrás evitar errores comunes al aplicar el teorema de Pitágoras y obtener resultados precisos en tus cálculos geométricos. Recuerda siempre identificar correctamente los lados del triángulo, utilizar la fórmula correcta, simplificar adecuadamente las operaciones y verificar los resultados obtenidos.

Conclusiones: Importancia y aplicaciones del teorema de Pitágoras

El teorema de Pitágoras es una de las herramientas más importantes en la geometría Euclidiana. Permite relacionar las longitudes de los lados de un triángulo rectángulo y su hipotenusa.

El teorema de Pitágoras, establece que en un triángulo rectángulo, el cuadrado de la hipotenusa (el lado de mayor longitud) es igual a la suma de los cuadrados de los otros dos lados. Esto se puede expresar matemáticamente de la siguiente manera:

a² + b² = c²

Este teorema es ampliamente utilizado en diversas aplicaciones prácticas, tanto en el ámbito de la física como en la ingeniería y la arquitectura.

Importancia del teorema de Pitágoras:

1. Permite calcular la longitud de un lado desconocido en un triángulo rectángulo cuando se conocen los valores de los otros dos lados.
2. Es utilizado en el diseño y construcción de estructuras, como puentes y edificios, para asegurar su estabilidad y resistencia.
3. Se aplica en la resolución de problemas trigonométricos, ayudando a calcular ángulos y distancias en diversas situaciones.
4. Es esencial en la navegación y la cartografía, ya que se utiliza en el cálculo de trayectorias y distancias entre puntos.

En conclusión, el teorema de Pitágoras es una herramienta fundamental en la geometría, con aplicaciones prácticas que van desde la resolución de problemas matemáticos hasta la construcción y la navegación. Su comprensión y dominio son clave en el desarrollo de diversas disciplinas y en la solución de múltiples situaciones cotidianas.