«`html
Las ecuaciones cuadráticas son un elemento fundamental en el álgebra y su resolución es crucial para comprender y aplicar conceptos matemáticos más avanzados. Una de las principales tareas al resolver una ecuación cuadrática es calcular el valor de x, que representa las soluciones de la ecuación. En este artículo, exploraremos detalladamente el proceso para calcular el valor de x en una ecuación cuadrática paso a paso, brindando una comprensión clara y profunda de este tema.
¿Qué es una ecuación cuadrática?
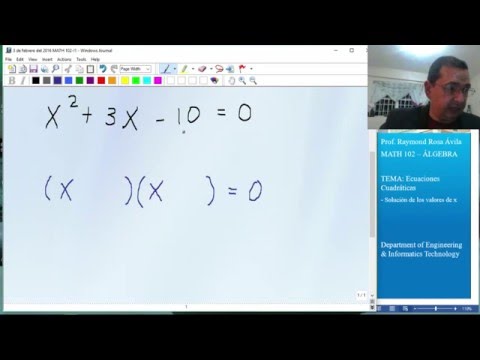
Antes de sumergirnos en el cálculo del valor de x, es esencial comprender qué es una ecuación cuadrática. Una ecuación cuadrática es una expresión matemática de la forma ax^2 + bx + c = 0, donde a, b y c son coeficientes, y x representa la variable desconocida que queremos resolver. Esta forma general de una ecuación cuadrática puede tomar varias formas, pero siempre incluirá términos al cuadrado y lineales.
La fórmula cuadrática
En el contexto de cálculo de valores de x en una ecuación cuadrática, la fórmula cuadrática juega un papel crucial. La fórmula cuadrática es una herramienta poderosa que nos permite encontrar las soluciones de cualquier ecuación cuadrática de forma rápida y precisa. La fórmula se expresa como x = (-b ± √(b^2 – 4ac)) / 2a, donde a, b y c son los coeficientes de la ecuación cuadrática.
Pasos para calcular el valor de x
Ahora que tenemos una comprensión básica de lo que implica una ecuación cuadrática, y entendemos la fórmula cuadrática, es hora de sumergirnos en el proceso detallado para calcular el valor de x. Aquí hay una guía paso a paso para abordar este proceso de manera efectiva.
Paso 1: Identificar los coeficientes a, b y c
El primer paso es identificar los coeficientes de la ecuación cuadrática. El coeficiente a es el término que acompaña a x^2, el coeficiente b acompaña a x, y c es el término independiente.
Paso 2: Sustituir los coeficientes en la fórmula cuadrática
Con los coeficientes correctamente identificados, sustituimos los valores de a, b y c en la fórmula cuadrática. Es crucial prestar atención al uso de los signos ± en la fórmula, ya que esto nos dará las dos posibles soluciones de la ecuación cuadrática.
Paso 3: Calcular el discriminante
El discriminante, representado por la parte bajo la raíz cuadrada en la fórmula cuadrática (b^2 – 4ac), nos brinda información sobre la naturaleza de las soluciones de la ecuación cuadrática. Es crucial calcular el discriminante para determinar si la ecuación tiene dos soluciones reales, una solución real o soluciones complejas.
Paso 4: Calcular las soluciones
Una vez que hemos determinado el valor del discriminante, procedemos a calcular las soluciones de la ecuación cuadrática utilizando la fórmula cuadrática. Es importante prestar atención a los signos ± en este paso, ya que nos darán las dos posibles soluciones.
Consideraciones adicionales
Mientras que los pasos mencionados anteriormente ofrecen un enfoque claro para calcular el valor de x en una ecuación cuadrática, es importante tener en cuenta algunas consideraciones adicionales.
Soluciones complejas
En algunos casos, es posible que las soluciones de la ecuación cuadrática sean complejas en lugar de reales. Cuando el discriminante es negativo, las soluciones serán números complejos. Esto es fundamental para comprender la naturaleza de las soluciones y no limitarse a los números reales.
Factorización
Otro enfoque para resolver ecuaciones cuadráticas implica la factorización. Al factorizar la ecuación cuadrática y establecer cada factor igual a cero, también podemos calcular los valores de x. Este método ofrece una perspectiva alternativa para abordar este tipo de ecuaciones.
Calcular el valor de x en una ecuación cuadrática es un proceso clave en el estudio de las matemáticas, y la comprensión de los pasos involucrados es fundamental para dominar este elemento del álgebra. Al seguir cuidadosamente la fórmula cuadrática y los pasos detallados proporcionados, podemos resolver ecuaciones cuadráticas y calcular las soluciones de manera efectiva. Esta habilidad es invaluable en numerosos contextos matemáticos y prácticos, lo que subraya la importancia de tener una comprensión clara y profunda de este proceso.
«`