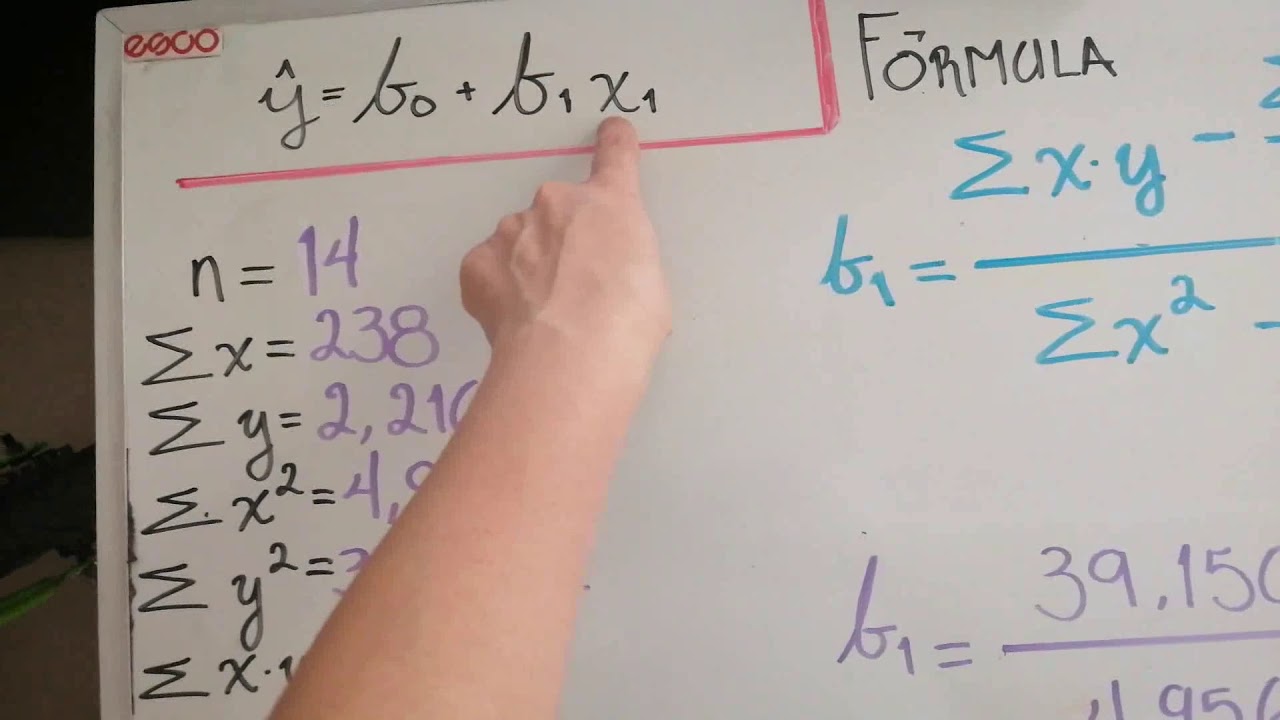La regresión lineal simple es una técnica estadística utilizada para comprender la relación entre una variable independiente y una variable dependiente. Es fundamental para el análisis de datos y la predicción de resultados. En este artículo, te llevaré a través de los pasos para calcular la ecuación de regresión lineal simple y comprender su aplicación en el mundo real.
Entendiendo la regresión lineal simple
La regresión lineal simple es una herramienta estadística que modela la relación entre una variable independiente (X) y una variable dependiente (Y) a través de una línea recta. La ecuación de regresión lineal simple es de la forma Y = a + bX, donde «a» es la intersección en Y (el valor de Y cuando X es 0) y «b» es la pendiente de la línea, que representa el cambio en Y por unidad de cambio en X.
Requisitos previos
Antes de calcular la ecuación de regresión lineal simple, es crucial comprender los conceptos básicos de la estadística, incluyendo la media, la desviación estándar y la covarianza. Además, es útil tener conocimientos de álgebra lineal para comprender los cálculos involucrados en la regresión lineal.
Recopilación de datos
El primer paso para calcular la ecuación de regresión lineal simple es recopilar los datos relevantes. Debes tener al menos un par de variables: una variable independiente (X) y una variable dependiente (Y). Estos datos pueden ser obtenidos de fuentes primarias o secundarias, dependiendo del contexto de tu análisis.
Cálculo de la covarianza
La covarianza es una medida de la relación lineal entre dos variables. Para calcular la ecuación de regresión lineal simple, necesitas determinar la covarianza entre la variable independiente (X) y la variable dependiente (Y). La fórmula para la covarianza es sumatoria[(X – X̄) * (Y – Ȳ)] / (n – 1), donde X̄ es la media de X, Ȳ es la media de Y, y «n» es el número de observaciones.
Cálculo de la varianza de X
La varianza de la variable independiente (X) es otra medida estadística importante para el cálculo de la regresión lineal simple. La fórmula para la varianza es sumatoria[(X – X̄)^2] / (n – 1), donde X̄ es la media de X y «n» es el número de observaciones.
Calculando la pendiente (b)
Una vez que tienes la covarianza y la varianza de X, puedes calcular la pendiente (b) de la ecuación de regresión lineal simple utilizando la fórmula: b = cov(X, Y) / var(X). La pendiente representa el cambio en la variable dependiente por unidad de cambio en la variable independiente.
Calculando la intersección en Y (a)
La intersección en Y (a) es el valor de Y cuando la variable independiente es 0. Puedes calcularla usando la fórmula: a = Ȳ – b * X̄, donde Ȳ es la media de Y, b es la pendiente calculada anteriormente, y X̄ es la media de X.
Obteniendo la ecuación de regresión lineal simple
Una vez que tienes la pendiente (b) y la intersección en Y (a), puedes construir la ecuación de regresión lineal simple: Y = a + bX. Esta ecuación te permite predecir el valor de la variable dependiente (Y) basándote en la variable independiente (X) utilizando la línea recta ajustada.
Interpretando los resultados
Es crucial interpretar los resultados de la ecuación de regresión lineal simple. La pendiente (b) determina la dirección y la pendiente de la relación entre las dos variables, mientras que la intersección en Y (a) es el valor de Y cuando X es 0. Estos parámetros proporcionan información importante sobre la relación entre las variables.
Aplicaciones y usos
La regresión lineal simple tiene numerosas aplicaciones en diversas áreas, como la economía, la psicología, la ingeniería y la ciencia de datos. Se utiliza para modelar y predecir fenómenos basados en la relación entre variables. Por ejemplo, en economía, se puede utilizar para predecir la demanda en función del precio de un producto.
Consideraciones y limitaciones
Es importante tener en cuenta las limitaciones de la regresión lineal simple, como asumir una relación lineal entre las variables, la sensibilidad a valores atípicos y la influencia de variables no consideradas en el modelo. Además, es esencial considerar cuidadosamente el contexto y la interpretación de los resultados.
En resumen, la regresión lineal simple es una herramienta estadística fundamental para comprender y modelar la relación entre variables. Calcular la ecuación de regresión lineal simple requiere pasos específicos, incluyendo el cálculo de la covarianza, la pendiente y la intersección en Y. La interpretación de los resultados y su aplicación en diversos campos son aspectos importantes a considerar al utilizar esta técnica. Espero que este artículo te haya proporcionado una comprensión clara de cómo calcular la ecuación de regresión lineal simple y su relevancia en el análisis de datos.