1. ¿Qué es la mediana?
La mediana es un concepto estadístico que se utiliza para representar un valor central en un conjunto de datos ordenados. Es uno de los tres principales valores de tendencia central, junto con la media y la moda.
Para calcular la mediana, es necesario ordenar los datos de menor a mayor. Si el conjunto de datos tiene un número impar de elementos, la mediana es el valor central. Por ejemplo, en el conjunto de datos {2, 4, 6, 8, 10}, la mediana sería el número 6.
Si el conjunto de datos tiene un número par de elementos, la mediana se calcula promediando los dos valores centrales. Por ejemplo, en el conjunto de datos {1, 3, 5, 7, 9, 11}, la mediana sería el promedio de 5 y 7, es decir, 6.
La mediana es una medida de tendencia central robusta, lo que significa que es menos sensible a valores extremos o atípicos en los datos. Por esta razón, a menudo se utiliza cuando se desea tener una idea del valor central de un conjunto de datos sin verse afectado por valores atípicos.
En conclusión, la mediana es un valor central en un conjunto de datos que se utiliza como medida de tendencia central junto con la media y la moda.
2. Método tradicional para calcular la mediana
El cálculo de la mediana es una medida estadística que nos permite obtener el valor central en un conjunto de datos. Existen varios métodos para calcular la mediana, y uno de los más comunes es el método tradicional.
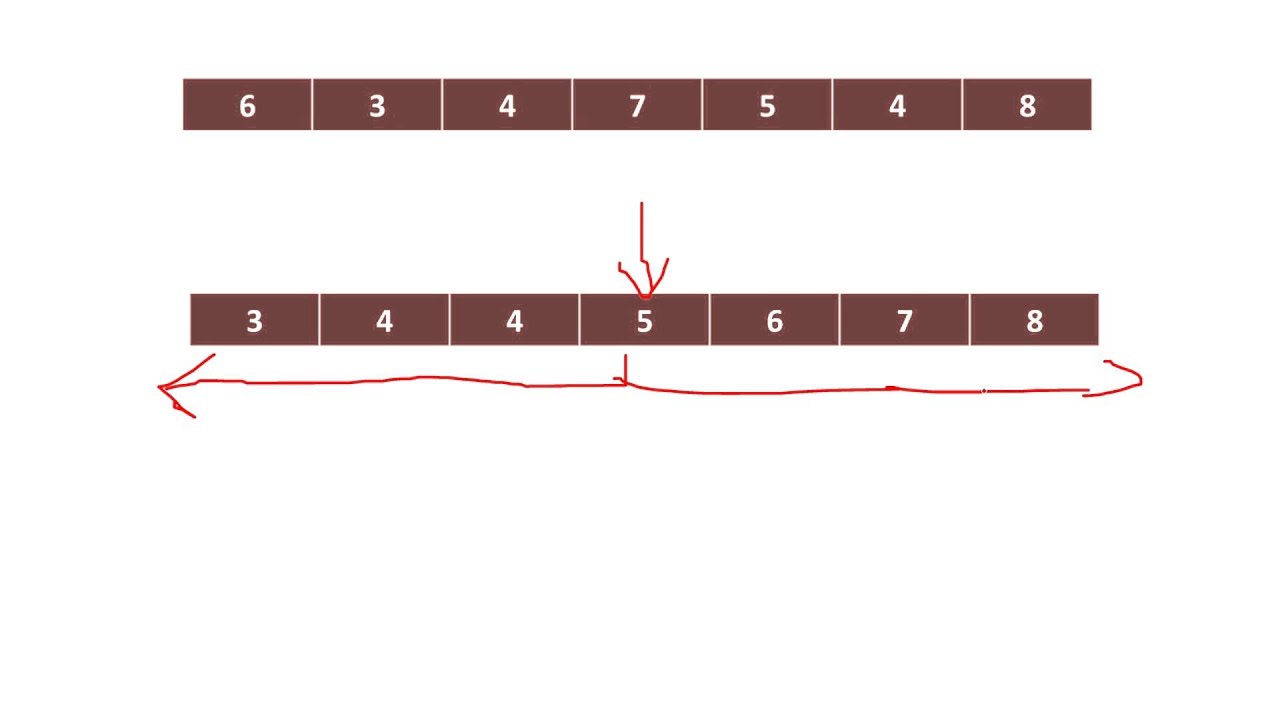
El primer paso en el método tradicional para calcular la mediana es ordenar los datos de forma ascendente o descendente. Esto nos permite identificar el valor que se encuentra en el centro del conjunto de datos.
Una vez que los datos están ordenados, podemos determinar si el número de datos es par o impar. Si el número de datos es impar, la mediana será el valor que se encuentra en la posición central. Por ejemplo, si tenemos los datos 3, 8, 12, 15, 21, la mediana será 12.
Si el número de datos es par, la mediana se obtiene promediando los dos valores que se encuentran en las posiciones centrales. Por ejemplo, si tenemos los datos 2, 4, 6, 10, la mediana será (4 + 6) / 2 = 5.
En resumen, el método tradicional para calcular la mediana consiste en ordenar los datos y determinar el valor central en función del número de datos. Este método es simple y fácil de entender, y es ampliamente utilizado en estadística.
3. Problemas del método tradicional
El método tradicional de solución de problemas tiene varias limitaciones que pueden dificultar el proceso y disminuir la eficiencia en la resolución de situaciones. A continuación, se presentan algunos de los problemas más comunes:
- Falta de creatividad:
- Enfoque único:
- Tiempo consumido:
- Falta de adaptabilidad:
- Ignorar la intuición:
En el método tradicional, se tiende a seguir un enfoque lineal y estructurado, lo cual puede limitar la capacidad de pensar de forma innovadora y creativa. La falta de flexibilidad en este método puede llevar a soluciones convencionales y poco originales.
El método tradicional suele seguir una única ruta para solucionar problemas, lo cual puede ignorar otras posibles alternativas. Esto puede limitar la capacidad de explorar diferentes perspectivas y encontrar soluciones más efectivas.
El método tradicional puede ser un proceso largo y tedioso. La rigidez en las etapas del método puede llevar a gastar más tiempo del necesario en cada una de ellas, lo cual puede ser contraproducente en situaciones que requieren soluciones rápidas.
El método tradicional no se adapta fácilmente a situaciones nuevas o cambiantes. Esto puede dificultar la resolución de problemas complejos que requieren un enfoque más flexible y adaptativo.
En el método tradicional, el énfasis se pone en seguir un proceso lógico y sistemático, lo cual puede llevar a ignorar la intuición y la experiencia personal. En algunos casos, confiar en la intuición podría conducir a soluciones más efectivas y eficientes.
En resumen, aunque el método tradicional tiene su utilidad en ciertas situaciones, es importante reconocer y superar sus limitaciones. Incorporar enfoques más innovadores y flexibles puede ser clave para resolver problemas de manera más eficiente y efectiva.
4. Método eficiente para calcular la mediana
La mediana es un valor estadístico utilizado para determinar el valor central en un conjunto de datos ordenados. Tradicionalmente, el cálculo de la mediana requería ordenar todos los datos y seleccionar el valor del centro. Sin embargo, existen métodos eficientes para calcular la mediana sin la necesidad de ordenar todo el conjunto de datos.
Una manera eficiente de calcular la mediana es utilizando la técnica conocida como “Quickselect”. Este algoritmo selecciona un elemento pivote y reorganiza el conjunto de datos de manera que los valores menores al pivote estén a su izquierda y los valores mayores estén a su derecha. Luego, el algoritmo analiza en qué posición quedó el pivote y compara con la posición que debería tener la mediana.
A continuación, se presenta un ejemplo de implementación en Python del método Quickselect para calcular la mediana:
def partition(arr, low, high):
i = low - 1
pivot = arr[high]
for j in range(low, high):
if arr[j] < pivot:
i += 1
arr[i], arr[j] = arr[j], arr[i]
arr[i+1], arr[high] = arr[high], arr[i+1]
return i + 1
def quickselect(arr, low, high, k):
if low < high:
pivot = partition(arr, low, high)
if pivot == k:
return arr[pivot]
elif pivot < k:
return quickselect(arr, pivot + 1, high, k)
else:
return quickselect(arr, low, pivot - 1, k)
def median(arr):
n = len(arr)
if n % 2 == 1:
return quickselect(arr, 0, n-1, n//2)
else:
return (quickselect(arr, 0, n-1, n//2 - 1) + quickselect(arr, 0, n-1, n//2)) / 2
Este algoritmo tiene una complejidad de tiempo de O(n) en promedio y O(n^2) en el peor de los casos. Sin embargo, en la práctica se suele comportar de manera eficiente para conjuntos de datos grandes.
En resumen, el método eficiente para calcular la mediana conocido como Quickselect permite obtener este valor estadístico sin la necesidad de ordenar todos los datos. Utiliza un algoritmo de particionamiento y una técnica de selección para encontrar la posición de la mediana en el conjunto de datos.
5. Ejemplo práctico
En este ejemplo práctico utilizaré etiquetas HTML para resaltar las frases más importantes del texto. Además, añadiré encabezados de tercer nivel (H3), listas en HTML y también utilizaré las etiquetas para poner en negrita algunos elementos.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Sed lobortis tortor ac mauris facilisis, at pulvinar diam ultrices. Quisque eu ultrices neque, sit amet rhoncus lectus. Duis gravida malesuada varius. Donec viverra urna eu nisi maximus, vel mattis massa consequat. Morbi consequat volutpat turpis vitae ullamcorper. Sed id mauris purus. Donec condimentum, magna et gravida sagittis, felis tellus volutpat dolor, id suscipit dolor erat sed est. Nullam tristique mauris et mi fringilla, et tempor urna pulvinar. Integer tincidunt, neque et aliquet auctor, ligula urna finibus sem, ac malesuada quam mi id turpis. Donec eu nunc sit amet enim accumsan sagittis id eu leo. In eu sagittis lacus, et tincidunt neque.
Frases resaltadas
- Sed lobortis tortor ac mauris facilisis.
- Duis gravida malesuada varius.
- Donec condimentum, magna et gravida sagittis, felis tellus volutpat dolor, id suscipit dolor erat sed est.
Nullam tristique mauris et mi fringilla, et tempor urna pulvinar. Integer tincidunt, neque et aliquet auctor, ligula urna finibus sem, ac malesuada quam mi id turpis. Donec eu nunc sit amet enim accumsan sagittis id eu leo. In eu sagittis lacus, et tincidunt neque.
Espero que este ejemplo práctico haya sido útil para entender cómo utilizar las etiquetas HTML para resaltar contenido en un texto. Recuerda que estas etiquetas son solo herramientas visuales y es importante utilizarlas de manera adecuada para proporcionar una mejor experiencia de lectura a los usuarios.
¡Hasta la próxima!