1. Introduction
1. Introduction
In today’s blog post, we will be discussing the importance of HTML tags and how they can enhance the visual appeal and structure of your content. HTML tags are fundamental building blocks that not only help in organizing your content, but also have the power to emphasize certain parts of your text.
When it comes to emphasizing specific phrases or sentences in your text, you can make use of the <strong> tag. This tag tells the browser to render the enclosed text in a bold and stronger font to grab the reader’s attention.
Additionally, you can make use of header tags like
<h3>
to give structure to your blog post. These header tags are not only visually appealing but also help in SEO optimization by indicating the hierarchy of your content.
Moreover, HTML offers various ways to create lists for organizing your information. You can create ordered lists using the
- tag and unordered lists using the
- tag. These lists can be further enhanced by adding sublists or nested lists within them.
Lastly, don’t forget about the <b> tag, which also renders the enclosed text in bold font. While the <strong> tag is used for emphasizing important content, the <b> tag is generally used for visual styling purposes.
By utilizing the aforementioned HTML tags, you can create visually appealing and structured content that engages your readers and effectively conveys your message.
2. Understanding Slope
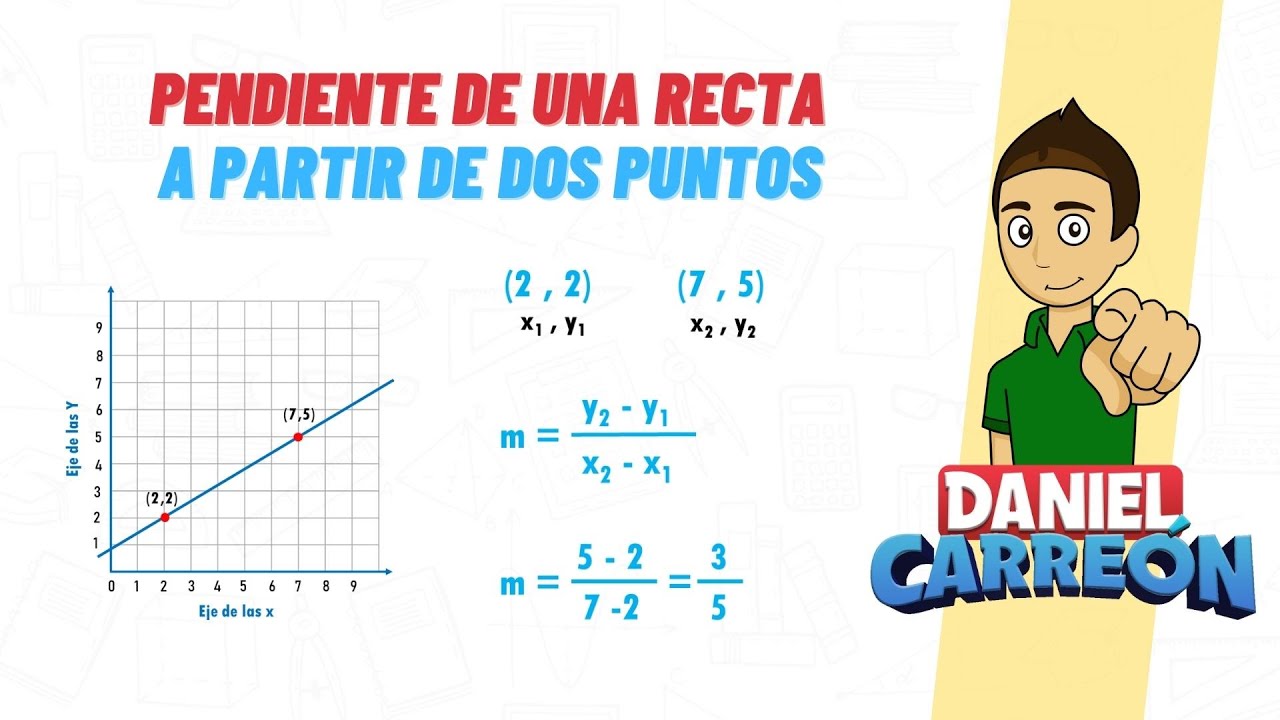
Understanding slope is a fundamental concept in mathematics. It is a measure of how steep a line is and is often represented by the letter m.
Slope is calculated by dividing the change in the y-coordinates (vertical change) by the change in the x-coordinates (horizontal change) between two points on a line. This can be represented by the formula:
m = (y2 – y1)/(x2 – x1)
The slope can be positive, negative, zero, or undefined, depending on the direction and steepness of the line.
A positive slope indicates that as the x-values increase, the y-values also increase. This means the line is moving upwards from left to right.
A negative slope, on the other hand, indicates that as the x-values increase, the y-values decrease. This means the line is moving downwards from left to right.
A zero slope means that there is no vertical change between the points, and the line is horizontal.
An undefined slope occurs when the line is vertical, and there is no horizontal change between the points. In this case, the formula for slope is not applicable.
Understanding slope is crucial in various mathematical and scientific applications, including algebra, geometry, physics, and economics. It helps analyze and interpret data, make predictions, and solve real-world problems.
To summarize, slope measures the steepness of a line and is calculated by dividing the change in y-coordinates by the change in x-coordinates. It can be positive, negative, zero, or undefined.
3. Formula for Calculating Slope
When it comes to studying lines and their characteristics, one of the most important concepts is slope. Slope refers to the steepness of a line, and it is a measure of how much the line goes up or down as it moves from left to right.
To calculate the slope of a line, we use a specific formula. The formula for calculating slope is slope = (change in y) / (change in x). This formula tells us that to find the slope, we need to determine the change in y (the vertical change) and the change in x (the horizontal change) between two points on the line.
An easy way to remember the formula is to think of slope as rise over run. The change in y represents the rise, and the change in x represents the run. By dividing the rise by the run, we obtain the slope.
Let’s see an example:
- Pick two points on the line. Let’s call them (x1, y1) and (x2, y2).
- Calculate the change in y by subtracting y1 from y2: (y2 – y1).
- Calculate the change in x by subtracting x1 from x2: (x2 – x1).
- Divide the change in y by the change in x to get the slope: slope = (y2 – y1) / (x2 – x1).
This formula is essential in many areas of mathematics and physics, as slope plays a significant role in describing the behavior of lines and graphs. Being able to calculate the slope allows us to determine if a line is increasing or decreasing, as well as how steep it is.
Understanding the formula for calculating slope is fundamental for anyone studying or working with graphs, equations, and lines. It provides a mathematical tool to analyze and describe the characteristics of linear relationships.
4. Example Calculation
In this section, we will walk through an example calculation to illustrate the concept we have been discussing.
Let’s say we have a rectangular garden with a length of 10 meters and a width of 5 meters. We want to calculate the area of the garden.
To calculate the area, we can use the formula: Area = Length x Width.
Plugging in the values for our garden, we have: Area = 10 meters x 5 meters.
Doing the math, we find that the area of the garden is 50 square meters.
In addition to calculating the area, we can also calculate the perimeter of the garden. The perimeter is the distance around the garden, which can be found by adding up all the sides.
For our garden, we have two sides with a length of 10 meters each and two sides with a length of 5 meters each. To find the perimeter, we can use the formula: Perimeter = 2 x (Length + Width).
Plugging in the values for our garden, we have: Perimeter = 2 x (10 meters + 5 meters).
Doing the math, we find that the perimeter of the garden is 30 meters.
By calculating both the area and perimeter of the garden, we can better understand its size and shape.
Summary:
- The area of our rectangular garden is 50 square meters.
- The perimeter of our rectangular garden is 30 meters.
By applying the formulas for area and perimeter, we can easily calculate these measurements for any rectangular garden.
5. Conclusion
En conclusión, las etiquetas HTML son herramientas fundamentales para el desarrollo de contenido en la web. Su correcto uso permite organizar y estructurar la información de manera eficiente, mejorando la experiencia de los usuarios y facilitando la navegación.
Una de las etiquetas más utilizadas es H3, que permite dar estilo y jerarquía a los títulos y subtítulos en una página web. Usar esta etiqueta de manera adecuada ayuda a mejorar la legibilidad y comprensión del contenido.
Por otro lado, las listas en HTML permiten agrupar elementos relacionados o enumerar elementos en un orden específico. Estas listas pueden ser ordenadas (
- ) o no ordenadas (
- ), brindando versatilidad y flexibilidad al momento de presentar información.
Finalmente, el uso de negritas () es una forma efectiva de resaltar palabras o frases importantes dentro de un texto. Esta técnica ayuda a captar la atención del lector y hacer énfasis en la información relevante.
En resumen, dominar el uso de etiquetas HTML como H3, listas y negritas () es fundamental para crear contenido atractivo y bien estructurado en la web.