Descomposición de fuerzas en dimensiones 2 y 3: Una Guía Paso a Paso
La descomposición de fuerzas en dimensiones 2 y 3 es un concepto fundamental en la física y la ingeniería. Al comprender cómo descomponer fuerzas de manera eficiente, los profesionales pueden abordar problemas de mecánica y estructuras con mayor precisión. En este artículo, exploraremos diferentes métodos para descomponer fuerzas en dimensiones 2 y 3, desde el uso de componentes rectangulares y coordenadas cartesianas hasta la aplicación de vectores tridimensionales. Acompáñanos en este viaje de descubrimiento y dominio de las herramientas fundamentales para el análisis de fuerzas.
La Importancia de la Descomposición de Fuerzas
Antes de sumergirnos en los detalles de la descomposición de fuerzas en dimensiones 2 y 3, es crucial comprender la importancia de este proceso en el análisis de sistemas físicos y estructurales. Las fuerzas presentes en un sistema pueden actuar en diferentes direcciones y planos, lo que requiere habilidades de descomposición para comprender su efecto global. La descomposición de fuerzas nos permite entender cómo actúan las fuerzas individuales en cada dirección, lo que es esencial para el diseño y la resolución de problemas en disciplinas como la ingeniería civil, mecánica y aeroespacial.
Descomposición de Fuerzas en Dos Dimensiones
Comencemos nuestro viaje explorando la descomposición de fuerzas en dos dimensiones. En este contexto, las fuerzas pueden ser descompuestas en componentes rectangulares, lo que facilita su análisis en términos de fuerzas horizontales y verticales.
Componentes Rectangulares: Método de descomposición primario
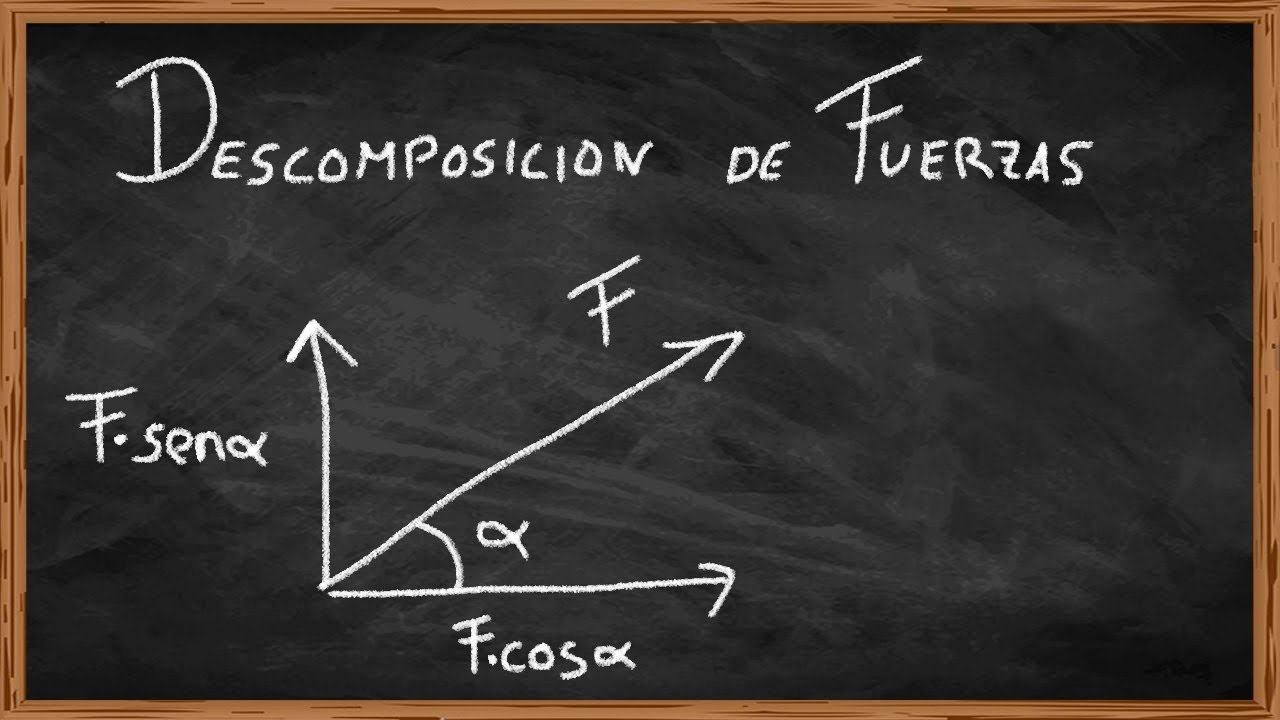
El método de componentes rectangulares es una herramienta fundamental para la descomposición de fuerzas en dos dimensiones. Al representar cada fuerza como la suma de sus componentes horizontal y vertical, podemos aplicar fácilmente las leyes de la física para analizar el equilibrio y el movimiento de un cuerpo. Este enfoque proporciona una comprensión clara de cómo actúan las fuerzas en diferentes direcciones, lo que es fundamental para resolver problemas de estática y dinámica.
Coordenadas Cartesianas: Abordaje matemático de la descomposición
En paralelo al método de componentes rectangulares, las coordenadas cartesianas ofrecen un enfoque matemático para la descomposición de fuerzas en dos dimensiones. A través de la representación de fuerzas en un plano cartesiano, podemos utilizar conceptos de trigonometría y álgebra para calcular con precisión las componentes de las fuerzas y su efecto resultante. Este enfoque es especialmente útil en situaciones donde se requiere un análisis detallado de fuerzas con ángulos no convencionales.
Descomposición de Fuerzas en Tres Dimensiones
Avanzando hacia la descomposición de fuerzas en tres dimensiones, nos adentramos en un espacio tridimensional donde las fuerzas pueden actuar en direcciones múltiples. La comprensión de la descomposición de fuerzas en tres dimensiones es esencial para el diseño de estructuras complejas y el análisis de sistemas tridimensionales.
Vectores Tridimensionales: Una perspectiva completa de las fuerzas
La descomposición de fuerzas en tres dimensiones requiere el uso de vectores tridimensionales para representar las fuerzas en un espacio tridimensional. Al utilizar vectores unitarios en dirección de x, y, y z, podemos descomponer una fuerza tridimensional en sus componentes respectivas en cada dirección. Este enfoque nos permite comprender cómo las fuerzas interactúan en un entorno tridimensional, lo que es esencial para el análisis estructural y de sistemas complejos.
Métodos Avanzados de Descomposición Tridimensional
Además de la representación mediante vectores tridimensionales, existen métodos avanzados para la descomposición de fuerzas en tres dimensiones, que incluyen el uso de matrices y cálculos tensoriales. Estos enfoques ofrecen una mayor capacidad para el análisis detallado de sistemas complejos, permitiendo a los ingenieros y físicos comprender a fondo cómo actúan las fuerzas en un entorno tridimensional y cómo afectan la estabilidad y el rendimiento de las estructuras y sistemas.
Aplicaciones Prácticas de la Descomposición de Fuerzas
Finalmente, es crucial explorar las aplicaciones prácticas de la descomposición de fuerzas en dimensiones 2 y 3. Desde el diseño de puentes y edificaciones hasta la ingeniería de dispositivos mecánicos y sistemas de transporte, la capacidad para descomponer y comprender las fuerzas en diferentes dimensiones es esencial para el éxito en numerosas disciplinas de ingeniería y ciencias aplicadas.
Innovación en el Diseño Estructural
La descomposición de fuerzas proporciona a los ingenieros la capacidad de diseñar estructuras innovadoras que pueden resistir fuerzas complejas y variables en diferentes direcciones. Al descomponer las fuerzas en dimensiones 2 y 3, los diseñadores pueden optimizar la eficiencia y la resistencia de sus creaciones, lo que resulta en avances significativos en el diseño estructural y la construcción.
Avances en la Ingeniería Aeroespacial y Mecánica
En el campo de la ingeniería aeroespacial y mecánica, la descomposición de fuerzas es fundamental para el diseño y la optimización de aeronaves, vehículos espaciales, y maquinaria industrial. La comprensión de cómo las fuerzas actúan en diferentes dimensiones permite a los ingenieros desarrollar soluciones innovadoras que maximizan el rendimiento y la seguridad de estas tecnologías avanzadas.
En resumen, la descomposición de fuerzas en dimensiones 2 y 3 es un concepto fundamental que desempeña un papel crucial en numerosas disciplinas científicas y de ingeniería. Al dominar las habilidades de descomposición de fuerzas, los profesionales pueden abordar desafíos complejos con confianza y precisión, generando avances significativos en el diseño, la construcción, y la innovación tecnológica. Continuar explorando y aplicando estos principios es esencial para el progreso continuo en el campo de la ciencia y la ingeniería.