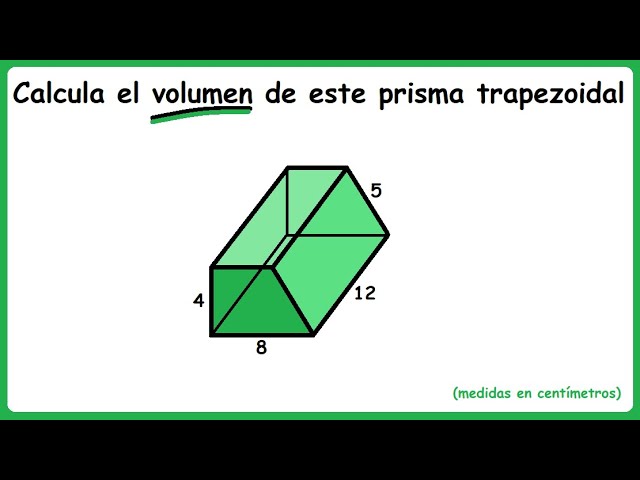
¿Qué es un prisma trapezoidal?
Un prisma trapezoidal es un tipo de prisma que tiene una base trapezoidal.
Un prisma es un sólido geométrico que tiene dos bases congruentes y paralelas, y caras laterales que son paralelogramos.
En el caso de un prisma trapezoidal, las bases son trapezoides, lo que significa que tienen dos lados paralelos y dos lados no paralelos.
Las caras laterales de un prisma trapezoidal son también trapezoides.
La altura de un prisma trapezoidal es la distancia entre las bases.
Para calcular el volumen de un prisma trapezoidal, se multiplica el área de la base trapezoidal por la altura.
Características principales de un prisma trapezoidal:
- Bases: Las bases del prisma trapezoidal son trapezoides.
- Caras laterales: Las caras laterales del prisma trapezoidal también son trapezoides.
- Altura: La altura del prisma trapezoidal es la distancia entre las bases.
- Volumen: El volumen de un prisma trapezoidal se calcula multiplicando el área de la base trapezoidal por la altura.
Los prismas trapezoidales pueden tener diferentes formas y tamaños, dependiendo de las dimensiones de sus bases y altura.
Son utilizados en diversas aplicaciones, como la construcción, la arquitectura y las matemáticas.
Fórmula para calcular el volumen de un prisma trapezoidal
Pasos para calcular el volumen de un prisma trapezoidal
Un prisma trapezoidal es un sólido geométrico con una base trapezoidal y caras laterales en forma de trapecio.
Para calcular el volumen de un prisma trapezoidal, se necesitan seguir los siguientes pasos:
Paso 1: Medir las dimensiones
Para comenzar, es importante medir las dimensiones del prisma trapezoidal.
Estas dimensiones incluyen la longitud de la base mayor (a), la longitud de la base menor (b), la altura del trapecio (h) y la altura del prisma (H).
Paso 2: Calcular la superficie de la base
El siguiente paso es calcular la superficie de la base del prisma trapezoidal.
Para ello, se utiliza la fórmula:
Superficie base = ((a + b) * h) / 2
Paso 3: Calcular el volumen
Una vez que se conoce la superficie de la base, se puede calcular el volumen del prisma trapezoidal.
Para ello, se utiliza la fórmula:
Volumen = Superficie base * H
Paso 4: Realizar la operación
Finalmente, se deben ingresar los valores medidos en las fórmulas y realizar la operación matemática.
Esto dará como resultado el volumen del prisma trapezoidal en unidades cúbicas.
Es importante recordar que todas las dimensiones deben estar en la misma unidad de medida para obtener un resultado correcto.
¡Y eso es todo! Siguiendo estos pasos, podrás calcular el volumen de un prisma trapezoidal de manera sencilla y precisa.
Ejemplo de cálculo de volumen
En este ejemplo aprenderemos cómo calcular el volumen de una figura geométrica sólida.
El volumen es una medida de la capacidad de un objeto, y se expresa en unidades cúbicas, como metros cúbicos o centímetros cúbicos.
Cálculo del volumen de un cubo
Para calcular el volumen de un cubo, necesitamos conocer la longitud de uno de sus lados.
El volumen se calcula elevando al cubo esta medida, es decir, multiplicando la longitud por sí misma dos veces.
La fórmula para calcular el volumen de un cubo es:
Volumen = Lado³
Donde Lado representa la longitud del lado del cubo.
Para ejemplificar esto, supongamos que el lado de un cubo mide 5 centímetros.
Podemos calcular el volumen utilizando la fórmula:
Volumen = 5³ = 5 * 5 * 5 = 125 cm³
Por lo tanto, el volumen del cubo es de 125 centímetros cúbicos.
Cálculo del volumen de una esfera
El cálculo del volumen de una esfera es un poco más complejo.
En este caso, necesitamos conocer el radio de la esfera.
El volumen se calcula utilizando la fórmula:
Volumen = (4/3) * π * Radio³
Donde Radio representa la longitud del radio de la esfera y π es una constante aproximada a 3.1416.
Supongamos que el radio de una esfera es de 10 metros.
Podemos calcular el volumen utilizando la fórmula:
Volumen = (4/3) * 3.1416 * 10³ = 4188.79 m³
Por lo tanto, el volumen de la esfera es de aproximadamente 4188.79 metros cúbicos.
Estos son solo dos ejemplos de cálculo de volumen, pero existen fórmulas similares para otras figuras geométricas.
Practicar el cálculo de volumen es una excelente manera de familiarizarse con las fórmulas y aplicarlas en problemas reales.